
- •Введение
- •1.2 Основные понятия и исходные положения
- •1.4 Понятия о перемещениях и деформациях
- •2.1 Статические моменты сечений
- •2.2 Моменты инерции сечений
- •2.2.2 Изменение моментов инерции сечения при повороте осей
- •2.3 Главные оси инерции и главные моменты инерции
- •2.4 Моменты инерции простых сечений
- •2.4.1 Прямоугольник
- •2.4.2 Треугольник
- •2.4.3 Круг
- •2.4.4 Кольцо
- •Вопросы для самопроверки
- •Вопросы для самопроверки
- •Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.
- •4.2.1 Линейное напряженное состояние
- •4.2.2 Плоское напряженное состояние
- •Рассмотрим частные случаи плоского напряженного состояния:
- •4.2.3 Объемное напряженное состояние
- •4.4 Теории прочности
- •Б) вторая теория прочности (теория наибольших деформаций).
- •В) третья теория прочности (теория наибольших касательных напряжений).
- •Вопросы для самопроверки
- •1. Построение эпюр крутящих моментов.
- •2. Напряжения в поперечном сечении.
- •3. Условия прочности и жесткости при кручении.
- •5.2 Напряжения в поперечном сечении
- •5.3 Условия прочности и жесткости при кручении вала
- •5.4 Потенциальная энергия деформации при кручении
- •Вопросы для самопроверки
- •Решение
- •6.2 Напряжение при чистом изгибе
- •6.3 Напряжения при поперечном изгибе
- •6.4 Перемещения при плоском изгибе
- •Вопросы для самопроверки
- •Перемещения в балках при чистом изгибе
- •Вопросы для самопроверки
- •8.1 Косой изгиб
- •8.2 Внецентренное растяжение (сжатие)
- •8.3 Кручение с изгибом
- •Вопросы для самопроверки
- •Определение критической силы
- •1. Динамическое действие нагрузок.
- •Вопросы для самопроверки
Вопросы для самопроверки
1. Что называется стержнем?
2. Какой вид нагружения стержня называются осевым растяжением (сжатием)?
3. Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?
4. Что такое эпюра продольных сил и как она строится?
5. Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня и по какой формуле они определяются?
6. Как связаны гипотеза плоских сечений (гипотеза Бернулли) и закон распределения нормальных напряжений в поперечном сечении растянутого (сжатого) стержня?
7. Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?
8. Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?
ТЕОРИЯ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ

Вопросы лекции:
1. Главные площадки и главные напряжения.
2. Виды напряженного состояния.
3. Обобщенный закон Гука.
4. Теории прочности.
4.1 Главные площадки и главные напряжения
Для того чтобы правильно оценить прочность бруса, необходимо уметь вычислять напряжение по любому сечению.
Через любую точку тела можно провести бесчисленное множество различно ориентированных площадок. При нагружении тела на этих площадках возникают в общем случае как нормальные, так и касательные напряжения.
Совокупность нормальных и касательных напряжений, возникающих на всем бесчисленном множестве площадок, которые можно провести через данную точку, характеризует напряженное состояние в этой точке.
Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.
Исследование напряженного состояния дает возможность анализировать прочность материала для любого случая нагружения тела.
Пусть в окрестности исследуемой точки шестью попарно параллельными плоскостями выделен элементарный прямоугольный паралле-лепипед с размерами ребер dx, dy и dz (рис.4.1). По его граням будут действовать нормальные “si” и касательные “tij” напряжения. Обозначения нормальных напряжений содержат один индекс - наименование оси, которой параллельно данное напряжение. В обозначении касательных напряже-
Рис. 4.1 ний используются два индекса: первый совпадает с
индек сом
нормального напряжения, действующее
сом
нормального напряжения, действующее
го по данной площадке, а второй – наименование
оси, которой параллельно данное касательное нап-
ряжение. Используем принятое правило знаков для
напряжений. Нормальное напряжение σ считается
положительным, если совпадает по направлению с
внешней нормалью n к площадке, касательные
напряжения t считаются положительными, если
вектор касательных напряжений следует поворачивать против хода часовой
стрелки до совпадения с внешней нормалью (рис.4.2). Отрицательными считаются напряжения обратных направлений (рис. 4.3).
Система сил, приложенных к элементарному кубу, должна удовлетворять условиям равновесия.
Рассмотрим элементарный параллелепипед размеров dx, dy, dz (рис. 4.1). Запишем уравнение равновесия параллелепипеда в виде суммы моментов относительно оси у (рис. 4.4), получим:

Аналогично
запишутся моменты сил относительно
осей x
и z.
Из этих уравнений следует, что
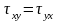 ,
,
 ,
,
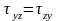 ,
т.е. на двух взаимноперпендикулярных
площадках составляющие касательных
напряжений, перпендикулярные к общему
ребру, равны и направлены либо к ребру,
либо от ребра. Этот вывод выражает закон
парности касательных напряжений, который
устанавливает зависимость между
величинами и направлениями пар касательных
напряжений, действующих по взаимно
перпендикулярным площадкам элементарного
параллелепипеда.
,
т.е. на двух взаимноперпендикулярных
площадках составляющие касательных
напряжений, перпендикулярные к общему
ребру, равны и направлены либо к ребру,
либо от ребра. Этот вывод выражает закон
парности касательных напряжений, который
устанавливает зависимость между
величинами и направлениями пар касательных
напряжений, действующих по взаимно
перпендикулярным площадкам элементарного
параллелепипеда.
С огласно
закону парности касательных напряжений
знаки
противоположны (рис. 4.4). Поэтому, если
площадку с напряжением
огласно
закону парности касательных напряжений
знаки
противоположны (рис. 4.4). Поэтому, если
площадку с напряжением
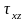 поворачивать
до совпаде-ния с площадкой с напряжением
поворачивать
до совпаде-ния с площадкой с напряжением
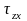 ,
то обязательно найдется такое положение
площадки, когда
= 0.
,
то обязательно найдется такое положение
площадки, когда
= 0.
Площадки, по которым касательные напряжения равны нулю, называются главными, а действующие по этим площадкам нормаль-
Рис.4.4 ные напряжения - главными напряжениями.
Главные напряжения обозначаются 1, 2, 3, причем 1 2 3. Элемент, выделенный главными площадками, изображен на рис. 4.5.
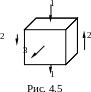
4.2 Виды напряженного состояния
В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.
