2.2.2 Изменение моментов инерции сечения при повороте осей

Найдем зависимость между моментами инерции относительно осей y, z и моментами инерции относительно осей y₁, z₁, повернутых на угол a. Пусть J_y > J_z и положительный угол a отсчитывается от оси y против часовой стрелки. Пусть координаты точки М до поворота – y, z, после поворота – y₁, z₁ (рис. 2.4).

Из рисунка следует:

; .

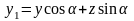Теперь определим моменты инерции относительно осей y₁ и z₁:

,

или

. (2.13)

Аналогично:

. (2.14)

(2.15)

Сложив почленно уравнения (2.13) и (2.14), получим:

т.е. сумма моментов инерции относительно любых взаимно перпендикулярных осей остается постоянной и не изменяется при повороте системы координат.

2.3 Главные оси инерции и главные моменты инерции

С изменением угла поворота осей a каждая из величин и меняется, а сумма их остается неизменной. Следовательно, существует такое значение

 = ₀, при котором моменты инерции достигают экстремальных значений, т.е. один из моментов инерции достигает своего максимального значения, в то время другой момент инерции принимает минимальное значение. Для нахождения значения ₀ возьмем первую производную от (или ) и приравняем ее нулю:

,

или ,

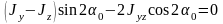откуда

. (2.16)

Покажем, что относительно полученных осей центробежный момент инерции равен нулю. Для этого приравняем правую часть уравнения (2.15) нулю:

,

откуда , т.е. получили ту же формулу для ₀.

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.

Обозначим главные оси через y₀ и z₀. Тогда

,

, (2.17)

.

Если сечение имеет ось симметрии, то эта ось всегда является одной из главных центральных осей инерции сечения.

 

2.4 Моменты инерции простых сечений

2.4.1 Прямоугольник

Определим момент инерции сечения относительно оси y₀, проходящей через центр тяжести прямоугольника высотой h и шириной b параллельно основанию (рис. 2.5). Выделим из прямоугольника линиями, параллельными оси y элементарную полоску высотой dz и шириной b. Площадь этой полоски dA=bdz, расстояние от полоски до оси y равно z. Подставим эти величины в выражение момента инерции относительно оси y (2.6):

_.

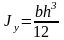. (2.18)

Аналогично, получим:

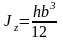. (2.19)

Очевидно, что ,

.
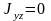