1.4 Понятия о перемещениях и деформациях

Под действием внешних сил любое тело деформируется, т.е. его форма и размеры изменяются, а точки тела меняют положение в пространстве.

П усть имеется тело с приложенными к нему силами F_i . Мысленно через точку a в направлениях осей X и Z проведем бесконечно малые отрезки ав и ас, длины которых dx и dz. После деформации бруса отрезки примут положение, изображенное штриховой линией (рис. 1.10). Точка а переместится в положение а₁. Величина аа₁, равная изменению координат точки называется линейным перемещением точки а. Отрезки ав и ас займут новые положения а₁в₁ и а₁с₁. Их длины изменяются на dx, и dz, которые называются абсолютными линейными деформациями.

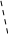z с₁

₁

dz₁ в₁

c а₁ dx₁

dz 

 в

а dx

x

Рис.1.10

Угол между начальным положением отрезка ав и конечным – а₁в₁ - называется угловым перемещением . Линейные перемещения измеряются в единицах длины, угловые - в радианах или градусах. Отношение приращения длины отрезка к его начальной длине представляет собой относительную линейную деформацию, т.е.

; .

Линейные деформации - величины безразмерные. Изменение первоначально угла между отрезками ав и ас после приложения к телу нагрузки, выраженное в радианах, представляет собой угловую деформацию  = ₁ - ₀.

Совокупность линейных деформаций  по различным направлениям и угловых деформаций  по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.

Вопросы для самопроверки

1. Что такое прочность, жесткость, устойчивость конструкции?

2. Что называется брусом, оболочкой, пластинкой?

3. Какая ось называется продольной осью бруса?

4. Что представляет собой расчетная схема конструкции и чем она отличается от собственно конструкции машины или аппарата?

5. Какие основные допущения в отношении свойств материала принимаются сопротивлении материалов?

6. В чем состоит принцип независимости действия сил?

7. В чем заключается гипотеза плоских сечений?

8. По каким признакам и как классифицируются нагрузки?

9. Какая нагрузка называется статической?

10. Что представляет собой интенсивность распределенной нагрузки?

11. В каких единицах измеряются сосредоточенные силы и моменты, интенсивности распределенных нагрузок?

12. Что такое внутренние силы (внутренние силовые факторы)?

13. Какие внутренние усилия (внутренние силовые факторы) могут возникать в поперечных сечениях брусьев, и какие виды деформаций с ними связаны?

14. В чем суть метода сечений?

15. Какие напряжения называются касательным и нормальным? Какова размерность напряжений? Каково правило знаков для напряжений?

16. Какова зависимость между полным, нормальным и касательным напряжениями в точке сечения?

17. Какова связь между напряжениями и внутренними силовыми факторами?

18. Какие деформации называются линейными, и какие угловыми?

Геометрические характеристики плоских сечений

Вопросы лекции:

1. Статические моменты сечений.

2. Моменты инерции сечений.

3. Главные оси инерции и главные моменты инерции.

4. Моменты инерции простых сечений.

К ак было показано выше, при растяжении и сжатии площадь поперечного сечения полностью характеризует прочность и жесткость стержня. Возьмем некоторое поперечное сечение бруса (рис. 2.1). Если представить себе сечение состоящим из бесчисленного множества площадок dA, то площадь всего сечения . Площадь является простейшей геометрической характеристикой сечения (размерность м²). Отметим два важных свойства: площадь всегда положительна и не зави-

Рис. 2.1 сит от выбора системы координат.

При расчетах на изгиб, кручение, сложное сопротивление и устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции сечений, которые зависят не только от формы и размеров сечений, но также от положения осей и точек (полюсов), относительно которых они вычисляются.