
- •Введение
- •1.2 Основные понятия и исходные положения
- •1.4 Понятия о перемещениях и деформациях
- •2.1 Статические моменты сечений
- •2.2 Моменты инерции сечений
- •2.2.2 Изменение моментов инерции сечения при повороте осей
- •2.3 Главные оси инерции и главные моменты инерции
- •2.4 Моменты инерции простых сечений
- •2.4.1 Прямоугольник
- •2.4.2 Треугольник
- •2.4.3 Круг
- •2.4.4 Кольцо
- •Вопросы для самопроверки
- •Вопросы для самопроверки
- •Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.
- •4.2.1 Линейное напряженное состояние
- •4.2.2 Плоское напряженное состояние
- •Рассмотрим частные случаи плоского напряженного состояния:
- •4.2.3 Объемное напряженное состояние
- •4.4 Теории прочности
- •Б) вторая теория прочности (теория наибольших деформаций).
- •В) третья теория прочности (теория наибольших касательных напряжений).
- •Вопросы для самопроверки
- •1. Построение эпюр крутящих моментов.
- •2. Напряжения в поперечном сечении.
- •3. Условия прочности и жесткости при кручении.
- •5.2 Напряжения в поперечном сечении
- •5.3 Условия прочности и жесткости при кручении вала
- •5.4 Потенциальная энергия деформации при кручении
- •Вопросы для самопроверки
- •Решение
- •6.2 Напряжение при чистом изгибе
- •6.3 Напряжения при поперечном изгибе
- •6.4 Перемещения при плоском изгибе
- •Вопросы для самопроверки
- •Перемещения в балках при чистом изгибе
- •Вопросы для самопроверки
- •8.1 Косой изгиб
- •8.2 Внецентренное растяжение (сжатие)
- •8.3 Кручение с изгибом
- •Вопросы для самопроверки
- •Определение критической силы
- •1. Динамическое действие нагрузок.
- •Вопросы для самопроверки
Вопросы для самопроверки
1. Какие перемещения получают поперечные сечения балок при прямом изгибе?
2. Запишите основное дифференциальное уравнение изогнутой оси балки.
3. Что называется жесткостью сечения при изгибе?
4. Как из основного (приближенного) дифференциального уравнения изогнутой оси балки получаются выражения углов поворота и прогибов ее сечений?
5. Из каких условий определяются постоянные интегрирования, входящие в уравнение углов поворота и прогибов сечений балки?
6. Запишите универсальное уравнение метода начальных параметров.
7. Перечислите основные для использования метода начальных параметров.
8. Что надо сделать, если распределенная нагрузка не доходит до правого конца балки?
Сложное сопротивление

Вопросы лекции:
1. Косой изгиб.
2. Внецентренное растяжение (сжатие).
3. Кручение с изгибом.
Ранее были рассмотрены виды нагружения, при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор: нормальная сила N - при растяжении, изгибающий момент Мy - при чистом изгибе, крутящий момент Мк - при кручении. Исключением явился лишь случай плоского изгиба (поперечный изгиб), при котором в поперечных сечениях стержня возникают одновременно два внутренних силовых фактора: изгибающий момент и поперечная сила. Но и в этом случае при расчетах на прочность и жесткость, как правило, учитывается только изгибающий момент. Эти виды нагружения - растяжение, изгиб и кручение, являются простыми.
Однако на практике часто встречаются и более сложные случаи, когда в поперечных сечениях стержня одновременно действует несколько внутренних силовых факторов, учитываемых при расчете на прочность (продольная сила и крутящий момент, крутящий и изгибающий моменты и т. п.). Эти случаи называют сложным сопротивлением.
Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.
Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:
- косой изгиб;
- внецентренное растяжение;
- изгиб с кручением.
При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения, действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.
8.1 Косой изгиб
Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.
Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как сочетание двух плоских изгибов во взаимно перпендикулярных плоскостях (рис.8.1).
Н
=
+
 ормальные
напряжения в любой точке поперечного
сечения могут быть вычислены как
алгебраическая сумма напряжений,
возникающих от моментов My
и Mz:
ормальные
напряжения в любой точке поперечного
сечения могут быть вычислены как
алгебраическая сумма напряжений,
возникающих от моментов My
и Mz:
 ,
(8.1)
,
(8.1)
где
 ,
,
 ,
,
j - угол отклонения плоскости действия M от вертикали.
Для определения положения опасной точки сечения и записи условия прочности необходимо записать уравнение нейтральной линии (н.л.) как геометрического места точек сечения, в которых напряжения равны нулю.
Уравнение нейтральной линии имеет вид:
 ,
или
,
или
 .
.
О
D
тсюда следует, что если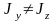 ,
то плоскость действия момента М
и нейтральная линия не перпендикулярны
друг другу (в отличие от плоского изгиба).
,
то плоскость действия момента М
и нейтральная линия не перпендикулярны
друг другу (в отличие от плоского изгиба).
М аксимального
значения в сечении нормальные напряжения
достигают в наиболее удаленных от
нейтральной линии точках В
и D
(рис. 8.2).
аксимального
значения в сечении нормальные напряжения
достигают в наиболее удаленных от
нейтральной линии точках В
и D
(рис. 8.2).
Эти точки являются опасными в данном сечении.
Условие прочности в т. B имеет вид:
 ,
(8.2)
,
(8.2)
где zB, yB - координаты точки B.
Для сечений, вписывающихся в прямоугольник (швеллер, двутавр и др.), в
точках с координатами ymax и zmax, условие прочности может быть записано в виде
 .
(8.3)
.
(8.3)
Прогиб при косом изгибе определяется как геометрическая сумма проги-
бов
вдоль осей
 и
и
 (рис. 8.3) по формуле
(рис. 8.3) по формуле
 .
.
 Направление
прогиба определяется углом
Направление
прогиба определяется углом
 .
.
Из формулы видно, что направления прогиба
балки будет совпадать с плоскостью действия
момента при Jz = Jy . Если моменты инерции се-
чения не равны между собой , то направ-
ление прогиба и положение плоскости действия
момента не совпадают (рис. 8.3).
