5.4 Потенциальная энергия деформации при кручении

Элементарная работа статически приложенного внешнего момента Т на перемещении d равна:

.

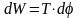При чистом кручении М_к = Т и .

Потенциальная энергия деформации

;

Интегрируя выражение для элементарной работы по всей длине l стержня, получим

.

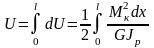При М_к = const и GJ_p = const, получим

. (5.10)

Вопросы для самопроверки

1. Какой вид нагружения называется кручением?

2. Что называется валом?

3. Как вычисляется скручивающий момент, передаваемый шкивом, по заданной мощности и числу оборотов в минуту?

4. Что такое эпюра крутящего момента и как она строится?

5. Перечислите гипотезы, принимаемые в теории кручения прямого вала круглого поперечного сечения.

6.  Какие напряжения возникают в поперечном сечении круглого вала при кручении и как они направлены?

7. Напишите формулу для определения напряжений в поперечном сечении скручиваемого круглого вала.

8. Какое напряженное состояние возникает в каждой точке круглого вала при кручении?

9. Напишите формулу для определения относительного и полного угла закручивания круглого вала.

10.     Что называется жесткостью сечения при кручении?

11. Что называется полярным моментом сопротивления, в каких единицах он выражается и чему равен (для круга и кольца)?

12.  Чем объясняется, что вал кольцевого сечения при кручении экономичнее вала сплошного сечения?

13. Чему равны наибольшие касательные напряжения и наибольшие главные напряжения в скручиваемом вале круглого сечения? В каких точках они возникают?

14.  Как разрушаются при кручении стальные чугунные и деревянные валы? Как объяснить характер разрушения для каждого из этих материалов?

15. Чему равна потенциальная энергия деформации кручения вала круглого сечения? Запишите соответствующую формулу.

16. Как производится расчет вала на прочность при кручении?

17. Как выбираются допускаемые напряжения при расчете на кручение?

18. Как производится расчет вала на жесткость при кручении?

 

Плоский изгиб

Вопросы лекции:

1. Построение эпюр поперечной силы и изгибающего момента.

2. Напряжения при чистом изгибе.

3. Напряжения при поперечном изгибе.

4. Перемещения при плоском изгибе

6.1 Построение эпюр поперечной силы и изгибающего момента

Если силы, действующие на стержень, перпендикулярны его оси, то стержень изгибается, или, говорят, работает на изгиб. Прямолинейный стержень, работающий на изгиб, называют балкой. Поперечное сечение балки может иметь любую форму, и для него, как известно, всегда можно построить пару взаимно перпендикулярных главных центральных осей инерции.

Наибольший практический интерес представляет случай, когда все внешние силы лежат в одной и той же плоскости, проходящей через одну из главных центральных осей инерции сечения. Возникающий при этом изгиб называют прямым плоским поперечным изгибом, а чаще просто изгибом. При этом изогнутая ось балки, называемая упругой линией, остается плоской кривой, лежащей в плоскости действия сил.

При изгибе одни продольные волокна балки растягиваются, другие сжимаются, а между ними есть слой волокон, которые не растянуты и не сжаты. Этот слой называют нейтральным, а линию пересечения нейтрального слоя балки с ее поперечным сечением - нейтральной линией, или нейтральной осью.

Нейтральная ось (н.о.) совпадает с той главной центральной осью инерции сечения, которая перпендикулярна плоскости действия сил (ПДС), как показано на рис. 6.1.

Рис. 6.1

В поперечных сечениях балки в общем случае возникают два внутренних силовых фактора  поперечная сила Q и изгибающий момент М, которые определяются из условий равновесия отсеченной (любой) части балки.

Поперечная сила Q_z в произвольном сечении балки равна алгебраической сумме всех внешних сил, приложенных к отсеченной части балки, т. е. действующих на балку по одну сторону от данного сечения:

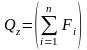_отсеч . (6.1)

Определяя поперечную силу в данном сечении, внешние силы, лежащие слева от сечения, берем со знаком плюс, если они направлены вверх, и со знаком минус, если  вниз. Для правой отсеченной части балки поступаем наоборот: внешние силы, лежащие справа от сечения, берем со знаком плюс, если они направлены вниз, и со знаком минус, если  вверх (рис. 6.2).

Рис. 6.2 Рис. 6.3

Это же правило можно сформулировать иначе: в выражении (6.1) внешние силы берутся со знаком плюс, если они стремятся повернуть рассматриваемую часть балки по часовой стрелке. Полученная при этом поперечная сила Q считается положи­тельной.

Изгибающий момент M_y в произвольном сечении балки равен алгебраической сумме моментов, взятых относительно центра тяжести сечения, всех внешних сил, приложенных к отсеченной части балки:

_отсеч. (6.2)

Определяя изгибающий момент в данном сечении, берем со знаком плюс те внешние моменты, которые вращают относительно центра тяжести сечения левую отсеченную часть балки по ходу часовой стрелки, а правую - против хода часовой стрелки. Полученный при этом изгибающий момент М считается положительным. Это правило иллюстрируется условным рисунком (рис. 6.3): изгибающий момент положителен, если внешние моменты изгибают ось балки выпуклостью вниз, сжимая верхние волокна балки. При этом следует мысленно защемить отсеченную часть балки в рассматриваемом сечении и разрешить ей изогнуться под действием приложенной к ней внешней силы.

При построении эпюр Q условимся положительные ординаты откла-дывать вверх от оси абсцисс, которая параллельна оси балки, а при построении эпюр М – вниз от оси абсцисс. При этом принятое правило знаков для изгибающего момента соответствует тому, что ординаты на эпюре М откладываются в сторону растянутого волокна. Знак на эпюре моментов можно не ставить. На эпюре Q знак ставится.

По эпюре изгибающих моментов определяется положение опасного сечения. Для балки с постоянным поперечным сечением опасным является то сечение, в котором возникает наибольший изгибающий момент М_max .

Изгиб, при котором в поперечных сечениях балки возникает только изгибающий момент, называется чистым изгибом.

Построение эпюр поперечных сил и изгибающих моментов производится в следующей последовательности:

1. Определяются опорные реакции (при расчете консольных балок этого можно не делать).

2. Определяется количество участков, подлежащих расчету (границами участков являются места приложения сосредоточенных сил и моментов, места

начала и конца действия распределенных нагрузок.

3. По участкам, используя метод сечений, составляются выражения для определения поперечных сил и изгибающих моментов.

4. В полученные выражения подставляются координаты характерных точек и определяются числовые значения поперечных сил и изгибающих моментов в этих точках.

5. По полученным числовым значениям строятся эпюры внутренних усилий и определяются опасные сечения.

Пример 6.1. Для заданной балки (рис. 6.4, а) построить эпюры Q и М, указать опасное сечение. Дано: а = 3 м, b = 2 м, с = 1 м, d = 4 м, F = 120 кН, М₁ = 20 кНм, М₂ = 120 кНм, М₃ = 20 кНм, q₁ = 20 кН/м, q₂ = 40 кН/м.