5.3 Условия прочности и жесткости при кручении вала

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде

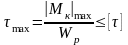. (5.6)

Из условия прочности можно определить диаметр вала:

- сплошного сечения

,

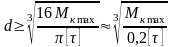- кольцевого сечения

.

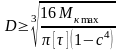Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак.

Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором ₁ = , ₂ = 0, ₃ = -, то при повороте граней элемента на 45⁰ в новых площадках обнаруживаются только нормальные напряжения, равные по величине t (рис. 5.6).

Р ассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис. 5.7, а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45⁰, т.е. по направлению действия максимальных растягивающих напряжений (рис. 5.7, б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис. 5.7, в).

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равными 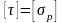- для хрупких материалов и 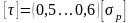- для пластичных материалов.

Анализируя эпюру касательных напряжений (рис. 5.4) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части, в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.

Из выражения (5.3) следует, что

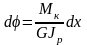. (5.7)

Интегрируя (5.7) по длине вала, получим:

.

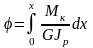Если крутящий момент М_к и жесткость вала GJ_p по всей длине постоянны, то

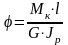, (5.8)

где GJ_p - жесткость вала при кручении.

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания

.

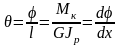Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:

(5.9)

Эта формула выражает условие жесткости вала при кручении. Обычно принимается [] = 0,5⁰ на 1 м длины вала.