Вопросы для самопроверки

1. Какое напряженное состояние называется пространственным (трехосным), плоским (двухосным) и линейным (одноосным)?

2. Каково правило законов для нормальных и касательных напряжений?

3. Сформулируйте закон парности касательных напряжений.

4. Чему равна сумма нормальных напряжений, действующих на любых двух взаимно перпендикулярных площадках?

5. Что такое главные напряжения и главные площадки? Как расположены главные площадки относительно друг друга?

6. Чему равны касательные напряжения на главных площадках?

7. Напишите формулы для определения главных напряжений и углов наклона главных площадок.

8. Как определить положение главной площадки, по которой действует главное напряжение s_max в общем случае плоского напряженного состояния?

9. Чему равны максимальные значения касательных напряжений в случае плоского напряженного состояния?

10. Какие площадки называются площадками сдвига и под каким углом они наклонены к главным площадкам?

11. Чему равна сумма нормальных напряжений на любых трех взаимно перпендикулярных площадках?

12. Чему равны максимальные и минимальные касательные напряжения (при заданных напряжениях s₁, s₂, s₃) и по каким площадкам они действуют?

13. Напишите формулы, обобщенного закона Гука?

14. На основе какого из допущений, принятых в курсе сопротивления материалов, получен обобщенный закон Гука?

15. Что называется полной удельной потенциальной энергией деформации, удельной потенциальной энергией изменения объема и формы?

16. Какой случай плоского напряженного состояния называется чистым сдвигом?

17. Напишите закон Гука при сдвиге.

18. Докажите, что объемная деформация при чистом сдвиге равна нулю.

19. Напишите зависимость между модулем упругости Е и модулем сдвига G.

20. Что называется предельным опасным состоянием материала? Чем характеризуется наступление опасного состояния для пластичных и хрупких материалов?

21. Какая точка тела называется опасной?

22. Что называется допускаемым напряженным состоянием?

23. Почему определение прочности в случаях сложного (плоского или пространственного) напряженного состояния приходится производить на основе результатов опытов, проводимых при одноосном напряженном состоянии?

24. Что представляют собой теории прочности?

25. Сформулируйте первую и вторую теории прочности. Укажите область применения.

КРУЧЕНИЕ ПРЯМОГО БРУСА

Вопросы лекции:

1. Построение эпюр крутящих моментов.

2. Напряжения в поперечном сечении.

3. Условия прочности и жесткости при кручении.

4. Потенциальная энергия деформации при кручении.

5.1 Построение эпюр крутящих моментов

Кручением называется вид нагружения, при котором к брусу прикладываются внешние скручивающие моменты, а в поперечных сечениях возникает единственный внутренний силовой фактор - крутящий момент M_к (рис.5.1).

Б русья, передающие крутящий момент, называются валами. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п. В большинстве случаев бывают заданы: мощность, передаваемая валом, и числом оборотов, а величины скручивающих моментов определяются исходя из этих данных.

Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N (Нм/с). Угловая скорость вращения вала равна (рад/сек), а передаваемая мощность . Тогда, скручивающий момент равен .

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

Крутящий момент М_к в сечении вала численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.

Рассмотрим вал, нагруженный скручивающими моментами Т₁=10кН×м, Т₂=25 кН×м, Т₃=35 кН×м (рис.5.2).

Воспользуемся методом сечений и:

1. Рассечем участки вала (рис.5.2). Границами участков являются точки приложения скручивающих моментов.

2. Отбросим правую отсеченную часть.

3. Заменим ее крутящим моментом М_к.

Из уравнения равновесия отсеченной части найдем величину крутящего момента М_к, возникающего в сечении.

1-ый участок

, .

2-ой участок

, кНм.

3-ий участок

,

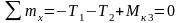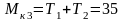кНм.

Для наглядного представления о величине крутящих моментов и характере их распределения по длине вала построим эпюры этих моментов. Построение эпюр крутящих моментов аналогично построению эпюр продольных сил при осевом растяжении-сжатии (рис.5.3).

Заметим, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.