Б) вторая теория прочности (теория наибольших деформаций).

Данная теория впервые была высказана французскими уче­ными Мариоттом и Навье, а затем поддержана Понселе и Сен-Венаном.

Согласно этой теории, в качестве критерия прочности принимают наибольшую по абсолютной величине деформацию. Предполагается, что нарушение прочности в общем случае на­пряженного состояния наступает тогда, когда наибольшая де­формация _max достигает своего опасного значения _пред. Последняя определяется при про­стом растяжении или сжатии образцов из данного материала.

Для пластичного материала условие прочности имеет вид

,

где .

Если, например, , то .

Для хрупкого материала условие прочности имеет вид

, .

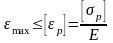Вторую теорию прочности можно сформулировать так: прочность материала при сложном напря­женном состоянии обеспечена, если наибольшая деформация не превышает допускаемой деформации при линейно напряженном состоянии.

Опытная проверка второй теории прочности свидетельст­вует о ее применимости лишь для хрупкого материала (легиро­ванный чугун, высокопрочная сталь после низкого отпуска).

В) третья теория прочности (теория наибольших касательных напряжений).

Появление на поверхности образца линий скольжения при возникновении пластических деформаций и разрушении мате­риалов при растяжении по наклонному сечению, где действуют наибольшие касательные напряжения, дает основание принять эти напряжения в качестве критерия прочности. Впервые такое предположение было высказано французским физиком Кулоном в 1773 г. и подтверждено опытами Треска, Геста и других уче­ных.

Третья теория прочности, называемая теорией наибольших касательных напряжений, предполагает, что предельное состоя­ние в общем случае наступает тогда, когда наибольшее каса­тельное напряжение _max достигает опасного значения _min (_min определяется при достижении предельного состояния в случае простого растяжения).

Условие прочности имеет вид:

,

где .

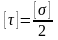Откуда .

Таким образом, третья теория прочности может быть сфор­мулирована следующим образом: прочность материала при сложном напряженном состоянии обеспечена, если наибольшее касательное напряжение не превышает допускаемого касатель­ного напряжения для линейного напряженного состояния.

Третья теория прочности достаточно хорошо подтвержда­ется опытами для пластичных материалов, одинаково работаю­щих на растяжение и сжатие. Недостаток ее заключается в том, что она не учитывает среднего по величине главного напряже­ния ₂, которое, как показывают эксперименты, также оказывает некоторое, хотя во многих случаях и незначительное, влияние на прочность материала.

г) четвертая теория прочности (теория наибольшей удельной потенциальной энергии формоизменения).

Рядом авторов было высказано предположение, что опас­ное состояние материала зависит не только от величины деформаций или напряжений в отдельности, а от их совокупности, т.е. от величины потенциальной энергии деформаций (которая вы­ражается через все три главных напряжения).

В конце XIX века итальянский ученый Бельтрами предложил в качестве критерия прочности принимать количество полной потенциальной энергии деформации в единице объема. Однако это предложение не нашло экспериментального подтверждения. В 1904 г. Губер, в 1913 г. Мезес и в 1924 г. Генки предложили в качестве критерия прочности принять не всю потенциальную энергию деформации, а только ту ее часть, которая идет на из­менение формы тела.

В связи с этим, в качестве критерия прочности принимается величина уде-льной потенциальной энергии формообразования, т.е. потенциальной энергии, идущей только на изменение фор­мы тела, не учитывающей деформации тела без искажения его формы.

В соответствии с этой теорией прочности нарушение проч­ности детали обусловлено переходом материала детали в пла­стическое состояние и появлением недопустимых пластических деформаций. Опасное состояние (текучесть) наступает тогда, когда удельная потенциальная энергия формоизменения дости­гает своего предельного значения.

Формулу удельной потенциальной энергии изменения формы получим из формулы полной удельной потенциальной энергии деформации (3.5), подставляя значение коэффициента Пуассона равного ν = 0,5.

Получим

,

Условие прочности имеет вид

,

где .

Откуда

Итак, согласно четвертой теории прочности, прочность ма­териала при сложном напряженном состоянии обеспечена, если наибольшая удельная потенциальная энергия формоизменения не превышает допускаемой удельной потенциальной энергии формоизменения для линейного напряженного состояния.

Опыты хорошо подтверждают третью и четвертую теорию прочности для пластичных материалов, одинаково работающих на растяжение и сжатие. Появление в материале малых пласти­ческих деформаций четвертой теорией определяется более точ­но, чем третьей.

д) теория прочности Мора.

Известно, что один и тот же материал в различных услови­ях нагружения ведет себя неодинаково, и деление материалов на хрупкие и пластичные имеет смысл только применительно к стандартным методам испытания образцов.

В настоящее время утвердилась точка зрения, согласно ко­торой каждый материал может разрушаться и хрупко, и пла­стично в зависимости от своей структуры, характера напряжен­ного состояния, соотношения главных напряжений, скорости нагружения, температуры и т.д. Следовательно, идеальной вы­глядела бы такая теория, которая охватывала бы оба состояния хрупкое и пластичное), конкретизируя при этом предельную стадию - разрушение или наступление текучести. Желательно также, чтобы учитывалось различие механических характери­стик при растяжении и сжатии, если такое наблюдается в экспе­рименте.

Теория Мора, отличающаяся от всех приведенных ранее, основана на предположении, что прочность материала в общем случае напряженного состояния, зависит главным образом от величины наибольшего ₁ и наименьшего ₃ главных напряже­ний, а среднее ₂ на прочность влияет незначительно.

Эта теория целиком базируется на опытных данных и не нуждается в дополнительной экспериментальной проверке.

Эквивалентное напряжение по этой теории определяется по формуле

_экв = ₁ - k₃,

где -для пластичных материалов.

Для хрупких материалов отношение заменяется на . Условие прочности запишется в виде:

₁ - k₃  []_p.

Наилучшие результаты эта теория дает для случая, когда ₁  0, а ₃  0. Это обстоятельство существенно, т. к. при решении практических задач напряженное состояние такого рода встречается чаще других. Для многих пластичных материалов, у которых _тр = _тс теория прочности Мора совпадает с теорией максимальных касательных напряжений.