10)Способы включения корректирующих звеньев для уменьшения ошибок в системе. Разновидности корректирующих обратных связей

Как было показано выше, коэффициенты ошибок Ci замкнутой системы полностью определяются коэффициентами передаточной функции WpW0 .Для обеспечения требуемых значений коэффициентов ошибки в замкнутую систему дополнительно включают корректирующие звенья с передаточной функцией WКЗ такой, чтобы результирующая передаточная функция WpW0 WКЗ обеспечила требуемые значения коэффициентов ошибки Ci .

Для расширения возможностей физической реализуемости передаточных функций корректирующих звеньев их можно включать по трем схемам (рис.6.3):

- последовательно (а),

- параллельно (б),

- по схеме с обратной связью (в).

При последовательной схеме соединений (рис.6.3.а) имеем: W=W1WКЗ, где W1 - передаточная функция исходной части схемы, W - желаемая для обеспечения малых ошибок передаточная функция. Тогда WКЗ=W/W1 .

Но полученная по этой формуле функция WКЗ физически может быть нереализуема. Тогда можно применить схему на рис. 6.3.б . Для того, чтобы обеспечить эквивалентность схем на рис. 6.3.а и 6.3.б , должно выполняться условие :

W1WКЗ = W1 + WП,

откуда выражение для передаточной функции корректирующего звена при параллельном способе включения будет иметь вид :

WП = W1 (WКЗ ~ 1), где WКЗ = W/W1.

Если и такой способ включения не решит проблему реализуемости функции WП , то можно применить схему на рис. 6.3.в . В этом случае должно выполняться условие :

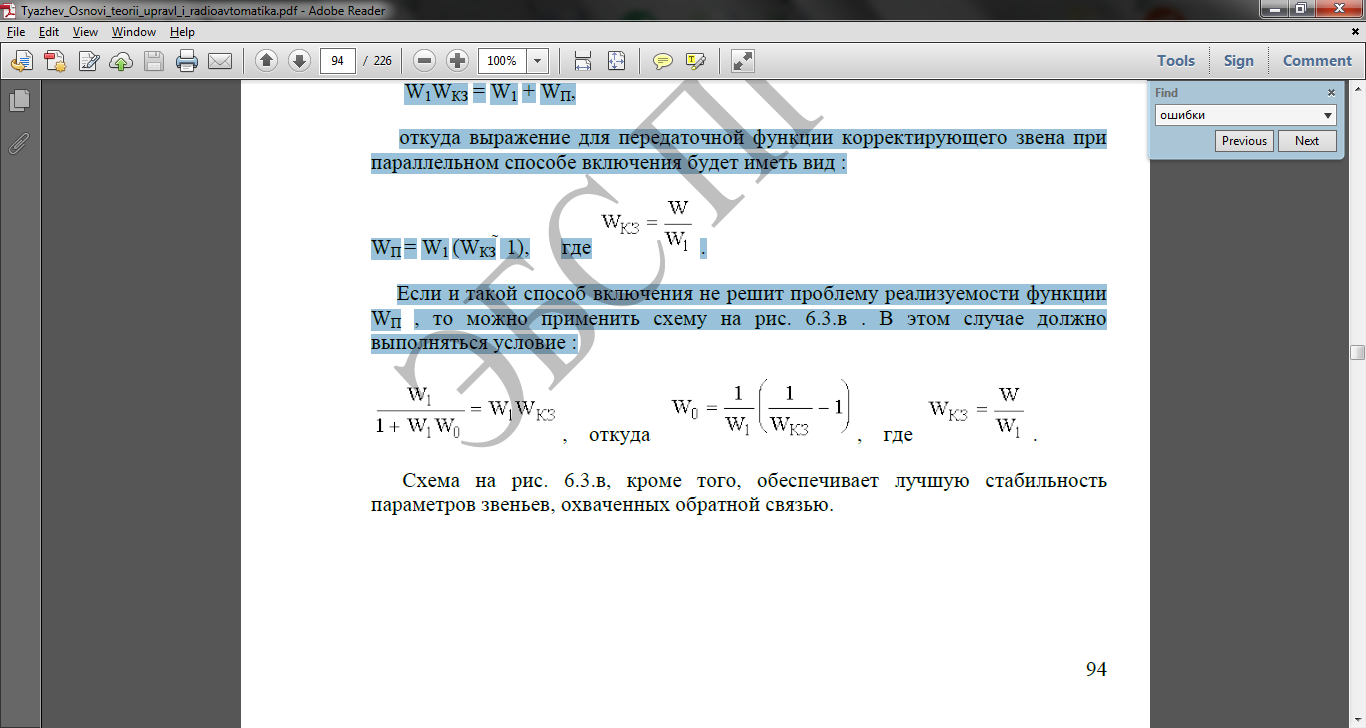
Схема на рис. 6.3.в, кроме того, обеспечивает лучшую стабильность параметров звеньев, охваченных обратной связью

Разновидности корректирующих обратных связей

Включение корректирующих звеньев по схеме с обратной связью (рис.6.3.в) позволяет изменить параметры охваченной обратной связью звеньев и даже изменить тип этих звеньев.

Покажем это на примерах.

Обратная связь называется жесткой, когда в цепи обратной связи включено безынерционное звено с передаточной функцией W0=k0. Если охватить такой ОС инерционное звено с передаточной функцией то результирующая передаточная функция будет равна

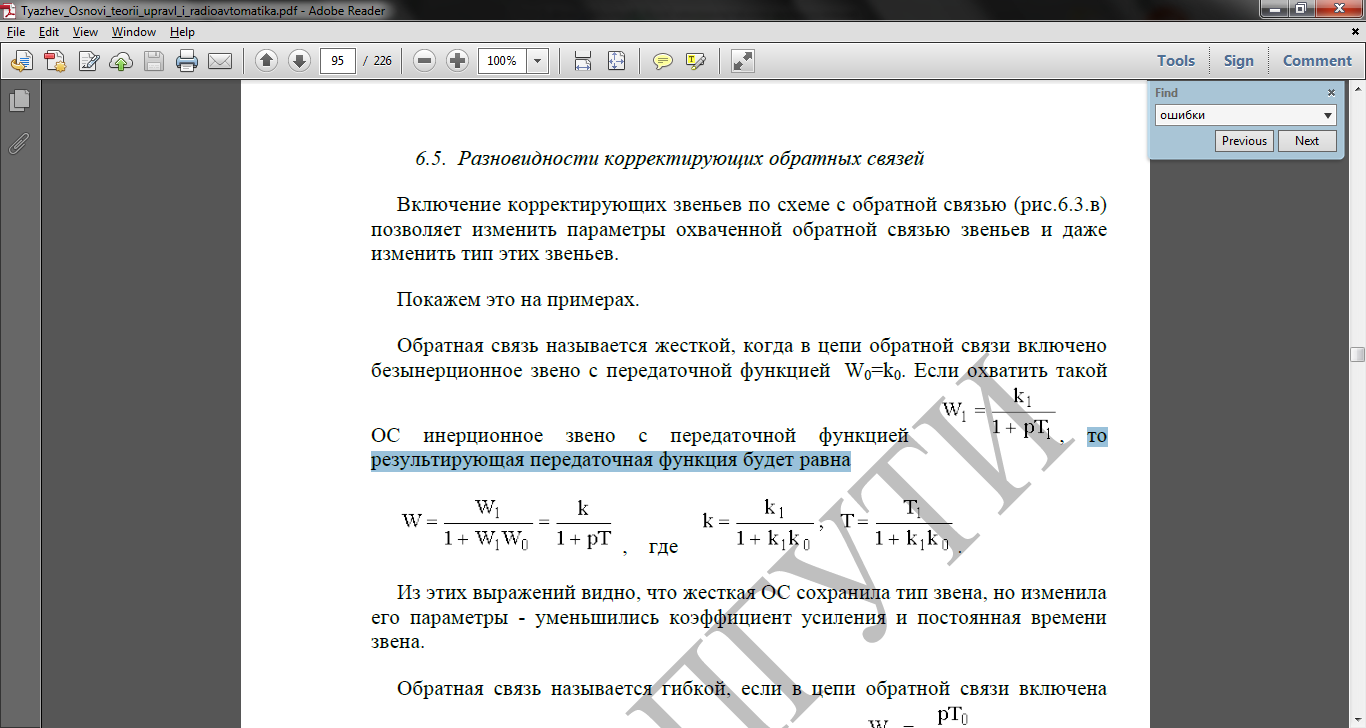
Из этих выражений видно, что жесткая ОС сохранила тип звена, но изменила его параметры - уменьшились коэффициент усиления и постоянная времени звена.

Обратная связь называется гибкой, если в цепи обратной связи включена дифференцирующая цепь с передаточной функцией

Охватим такой ОС усилитель с передаточной функцией W1=k1. В результате получим

Это выражение передаточной функции для корректирующего звена с отставанием по фазе с параметром =1+k1. // абсолютно без понятия, что кроется за этим символом

Если гибкой ОС охватить интегратор, у которого W1=kи /p , то в результате получим

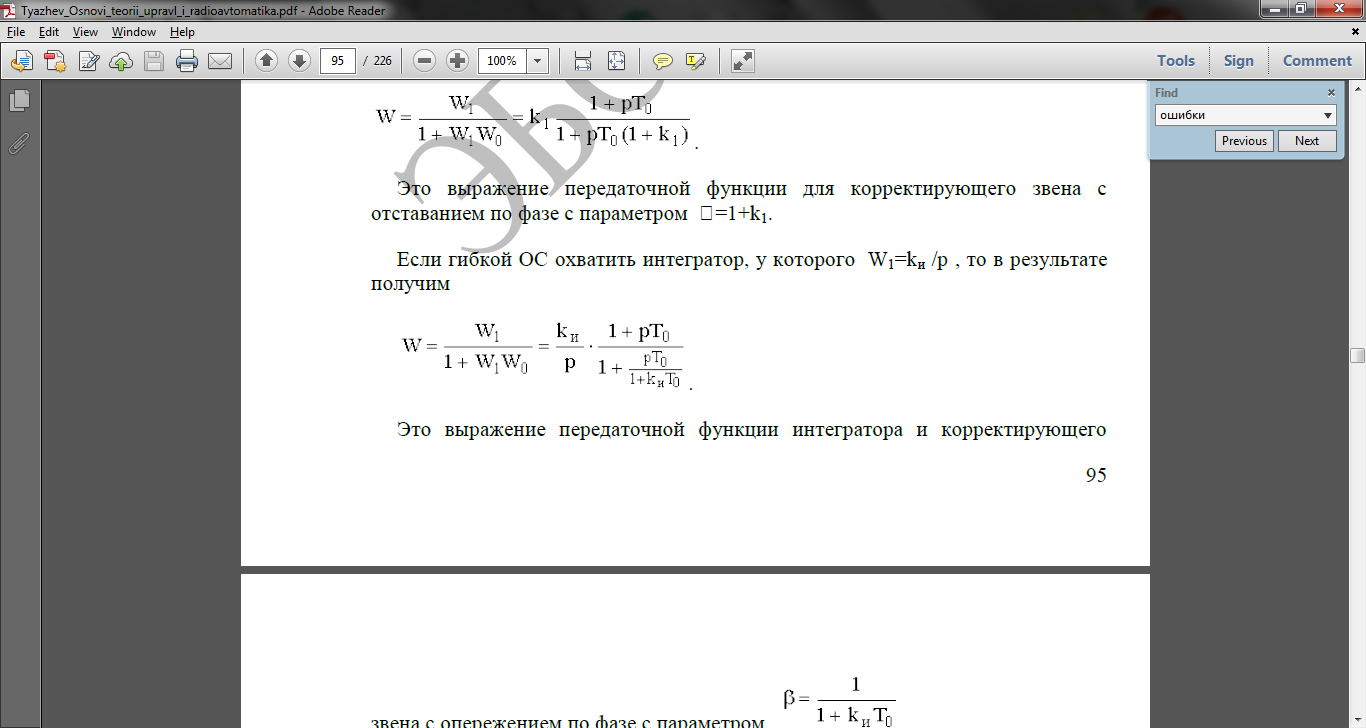
Это выражение передаточной функции интегратора и корректирующего

звена с опережением по фазе с параметром 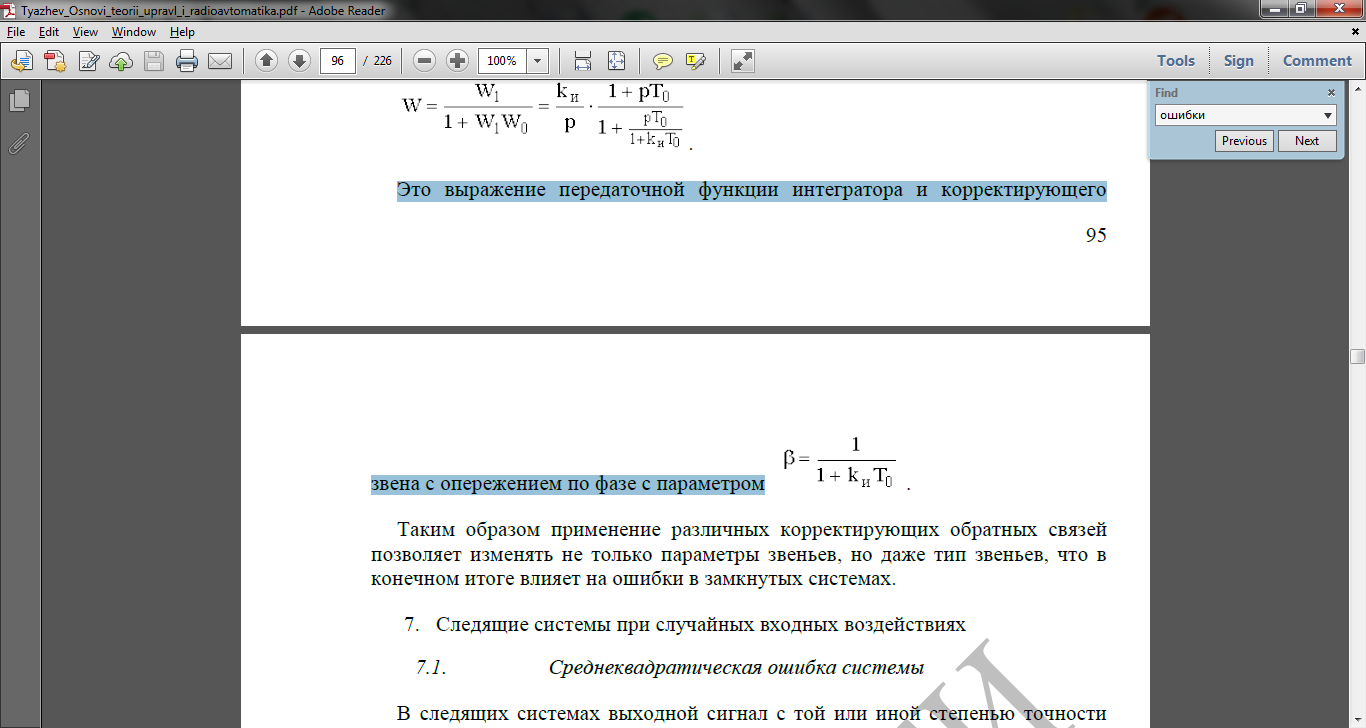Таким образом применение различных корректирующих обратных связей позволяет изменять не только параметры звеньев, но даже тип звеньев, что в конечном итоге влияет на ошибки в замкнутых системах.