2 Вариант (тяжев) // не так подробно, но более менее понятно
Этот
критерий позволяет судить об устойчивости
замкнутой системы по годографу разомкнутой
системы. Критерий Найквиста гласит:
если годограф ККП разомкнутой системы
при изменении частоты от нуля до
бесконечности не охватывает на комплексной
плоскости P(w);
jQ(w)
точку с координатами -1; j0, то замкнутая
система, собранная по схеме рис. 5.3.а,
будет устойчива. В противном случае
замкнутая система будет неустойчива.
Для замкнутой системы, образованной по
схеме рис. 5.3.б, вместо годографа
рассматривается годограф
На рис. 5.7 приведены годографы устойчивой и неустойчивой замкнутых систем.
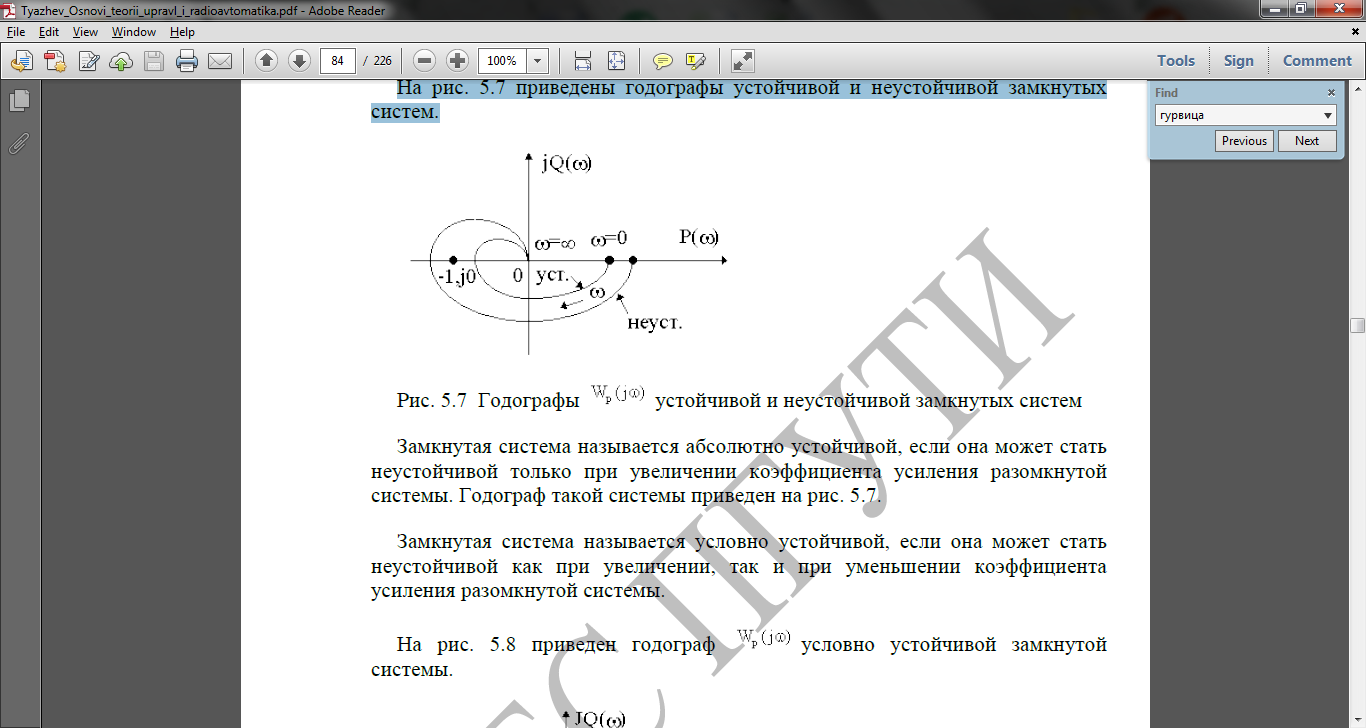
Замкнутая система называется абсолютно устойчивой, если она может стать неустойчивой только при увеличении коэффициента усиления разомкнутой системы. Годограф такой системы приведен на рис. 5.7.
Замкнутая система называется условно устойчивой, если она может стать неустойчивой как при увеличении, так и при уменьшении коэффициента усиления разомкнутой системы
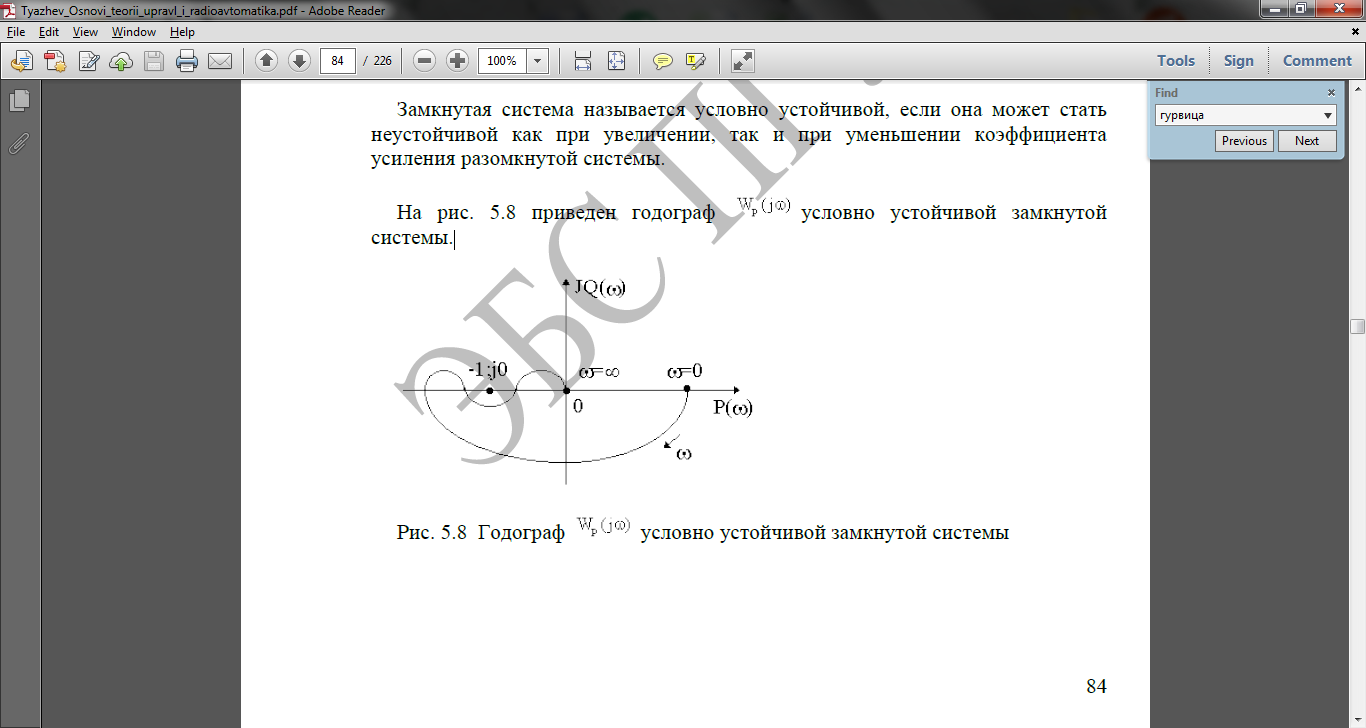
8) Статические ошибки в замкнутых системах автоматического управления
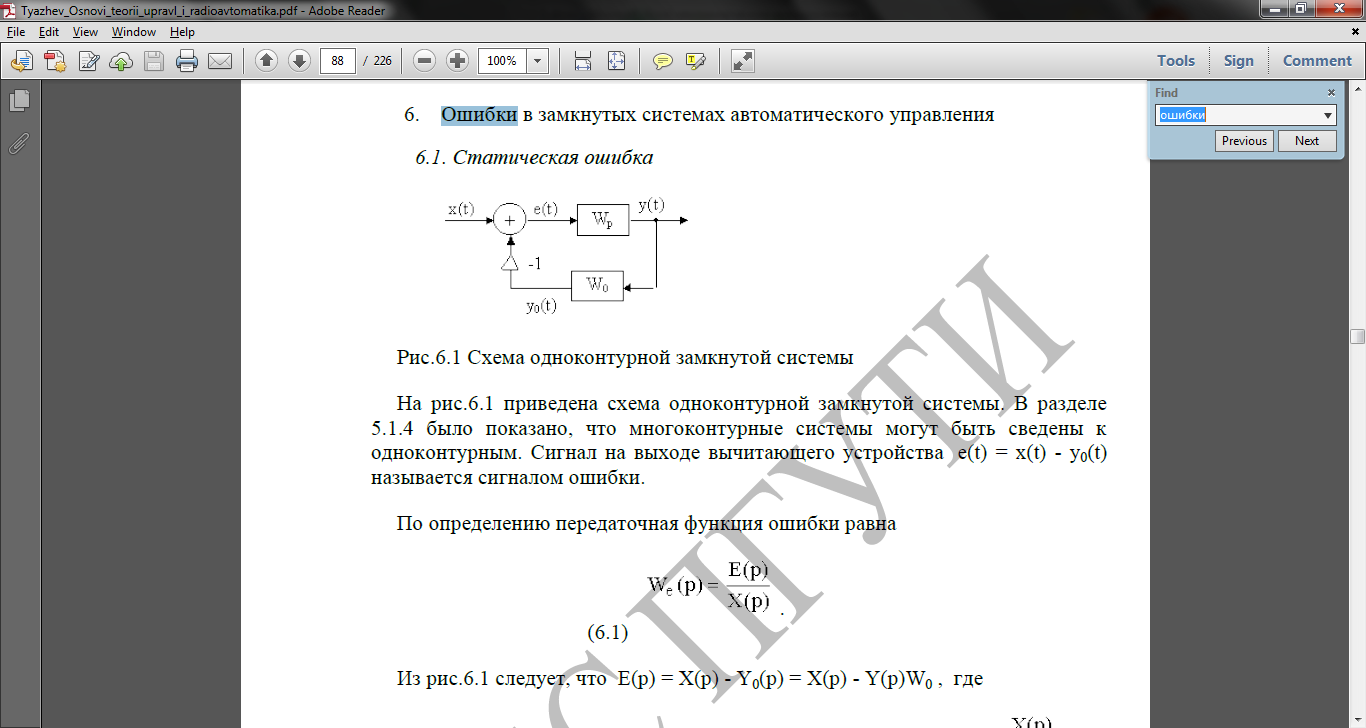
На рис.6.1 приведена схема одноконтурной замкнутой системы. В разделе 5.1.4 было показано, что многоконтурные системы могут быть сведены к одноконтурным. Сигнал на выходе вычитающего устройства e(t) = x(t) - y0(t) называется сигналом ошибки.
По определению передаточная функция ошибки равна
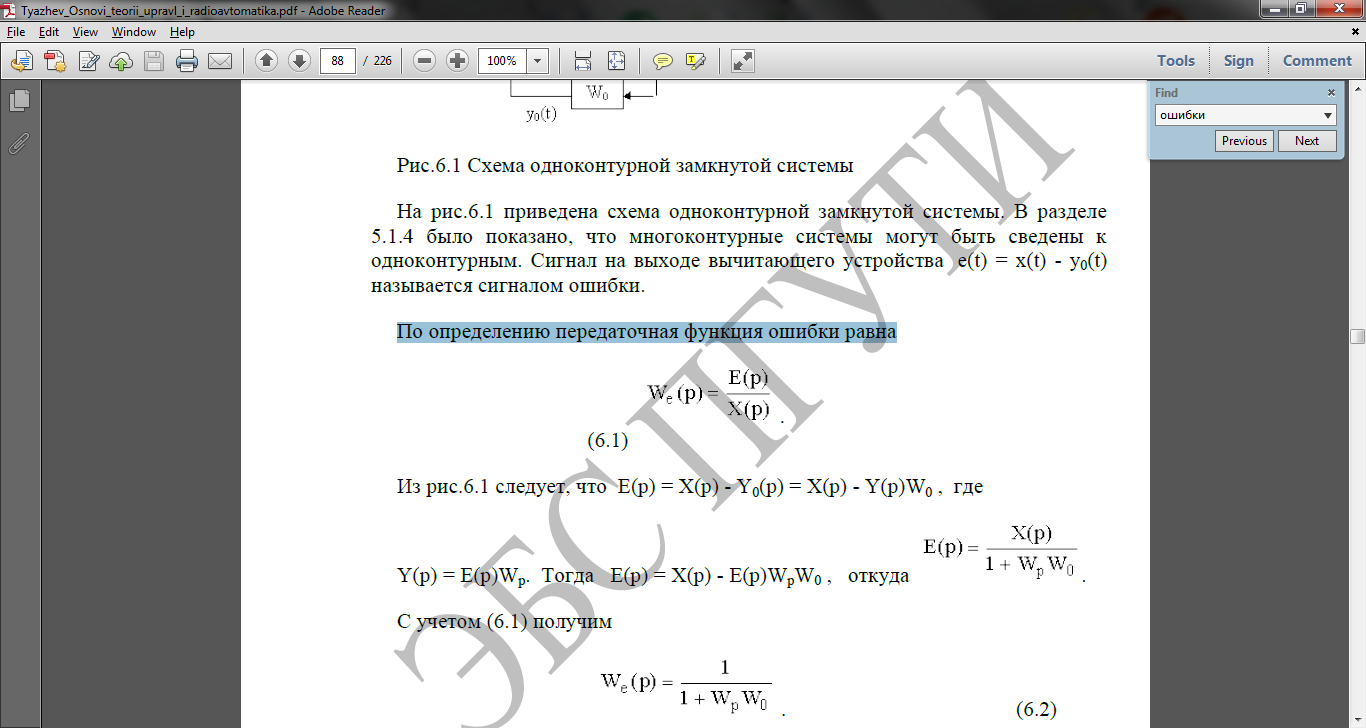
Из рис.6.1 следует, что E(p) = X(p) - Y0(p) = X(p) - Y(p)W0 , где
Y(p)
= E(p)Wp.
Тогда E(p) = X(p) - E(p)WpW0
, откуда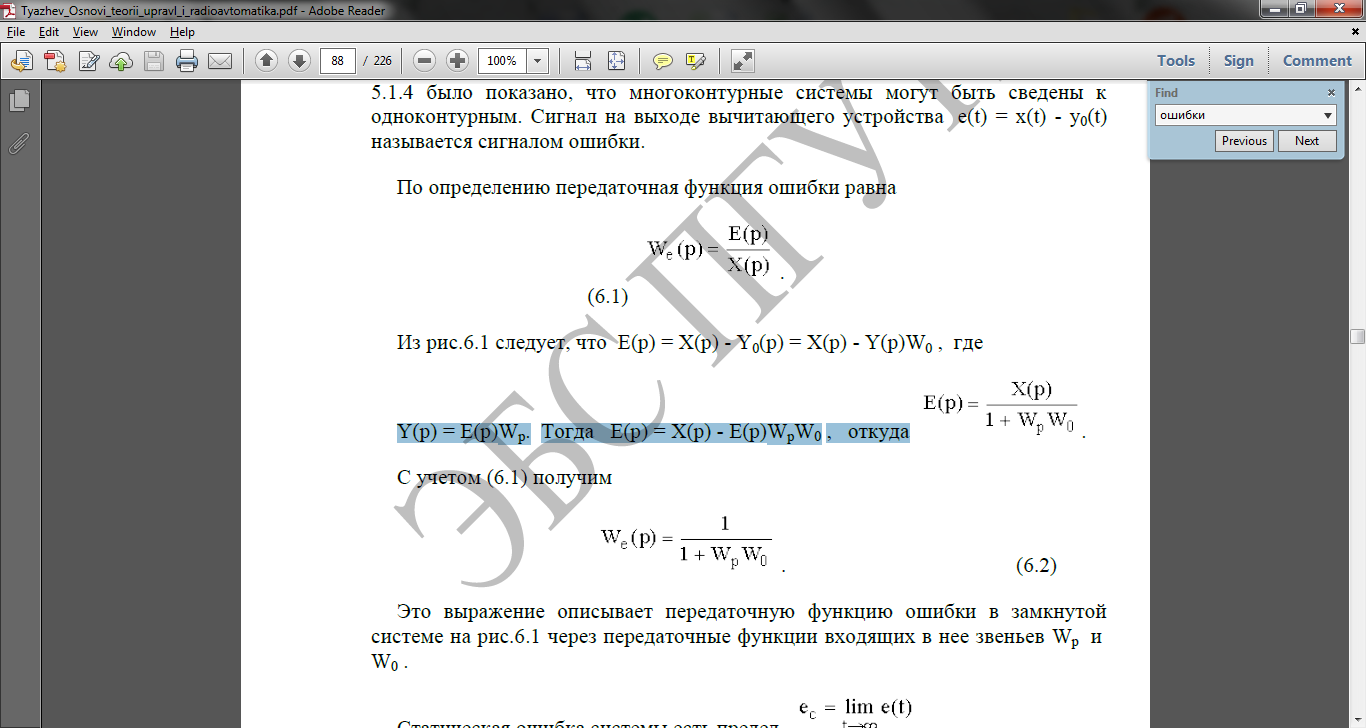
С учетом (6.1) получим
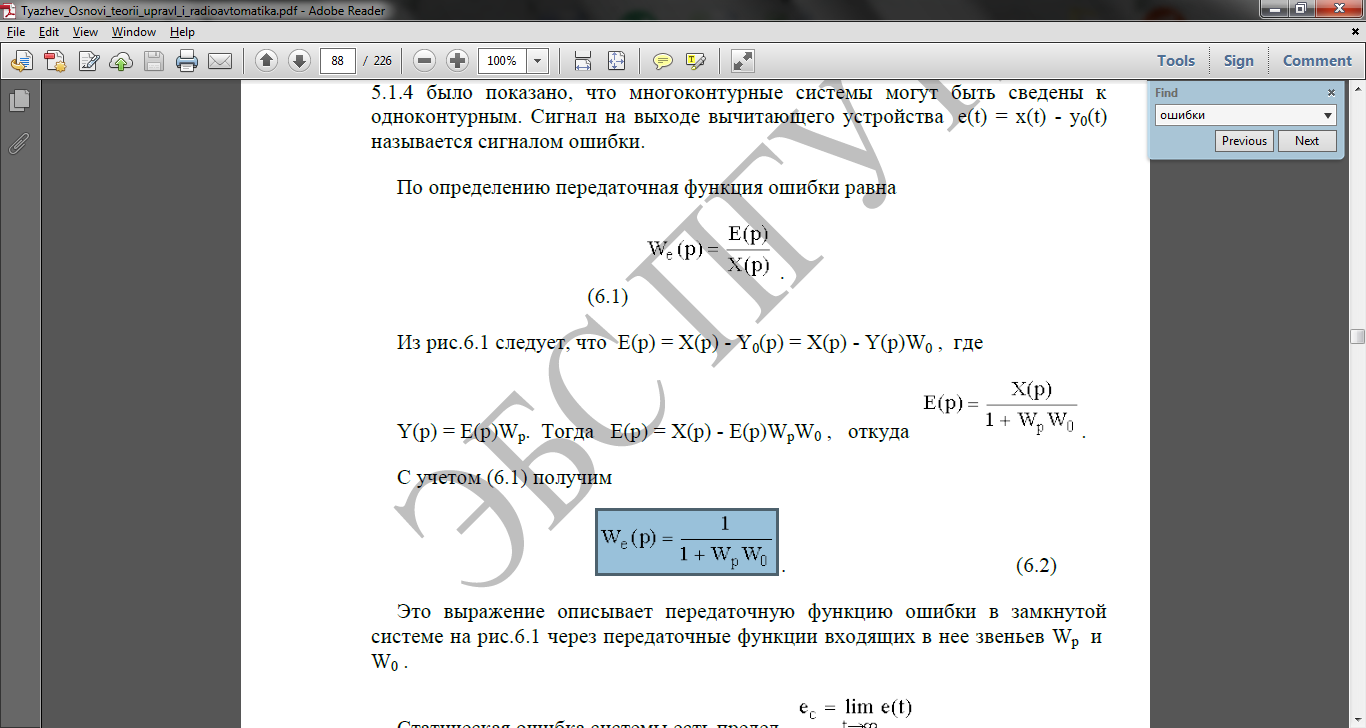
Это выражение описывает передаточную функцию ошибки в замкнутой системе на рис.6.1 через передаточные функции входящих в нее звеньев Wp и W0 .
Статическая
ошибка системы есть предел
При входном сигнале
Так
как X(p) = C/p , то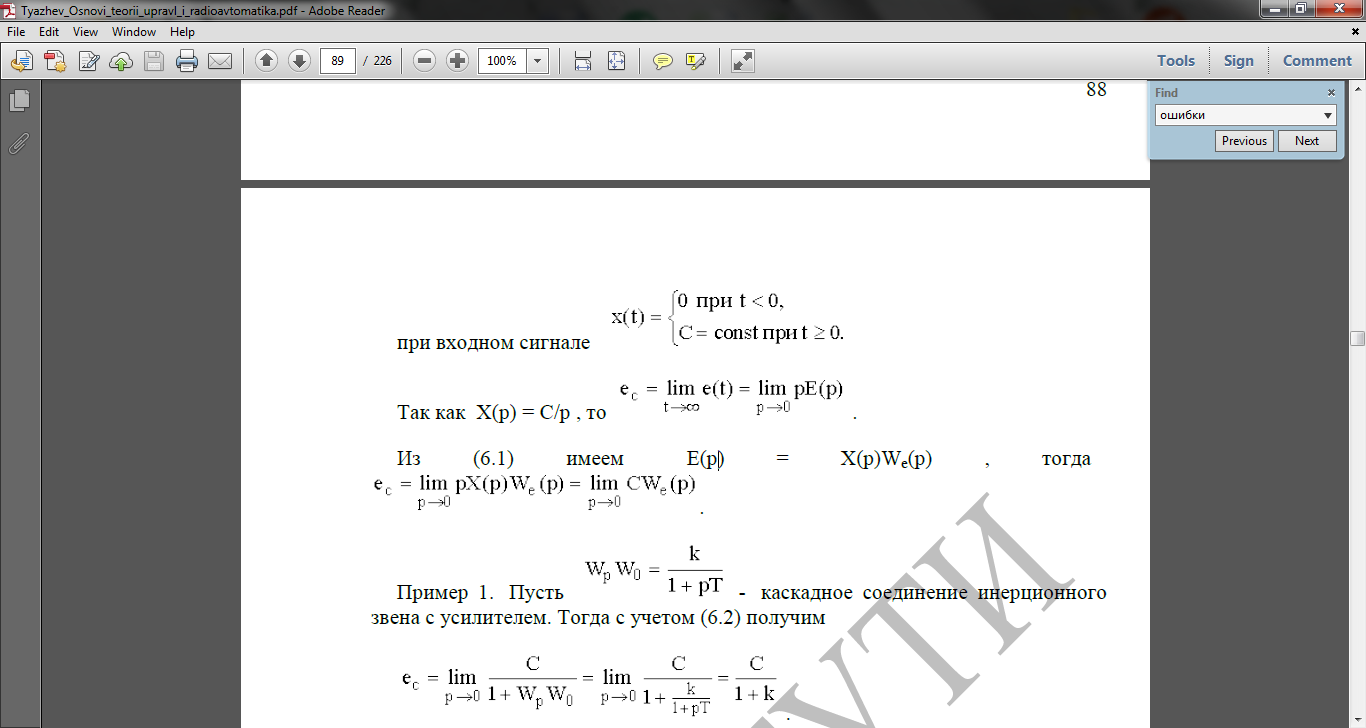
Из (6.1) имеем E(p) = X(p)We(p) , тогда
9) Динамические ошибки систем автоматического управления. Способы определения коэффициентов ошибок
Динамическими называются ошибки в замкнутой системе при входном воздействии вида
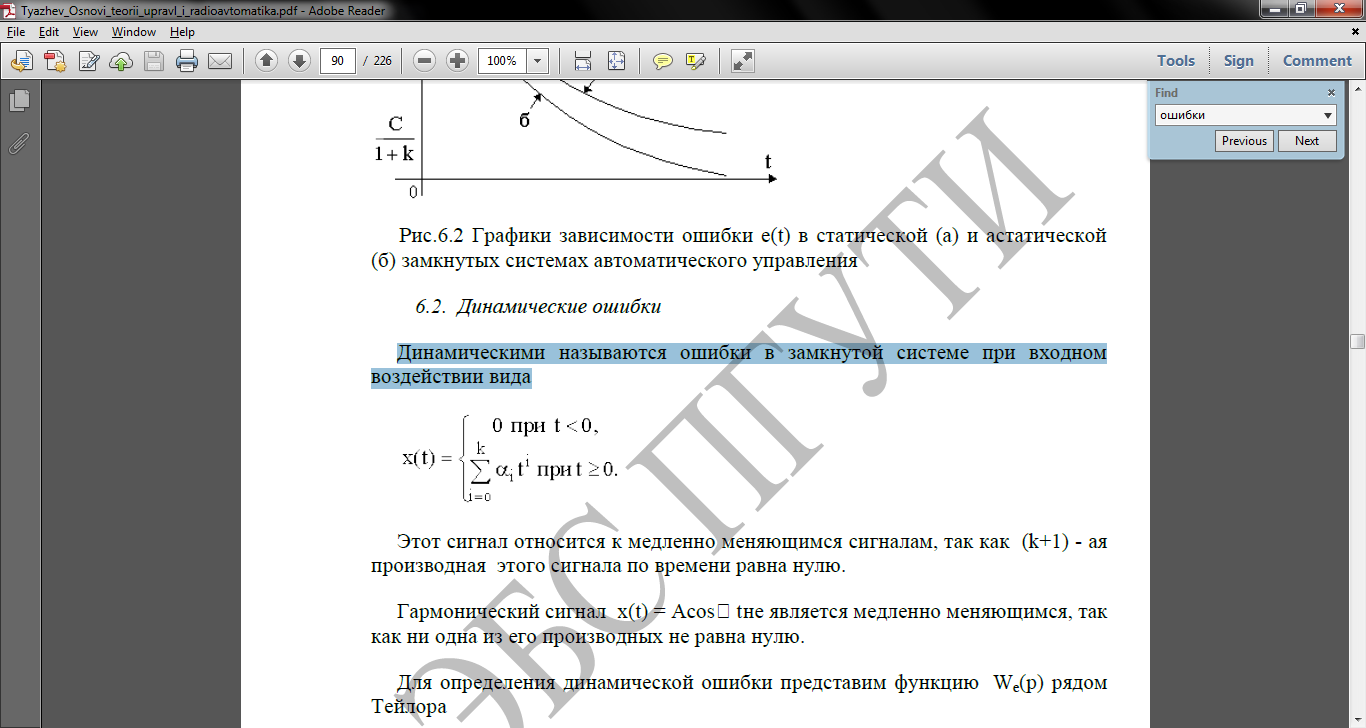
Этот сигнал относится к медленно меняющимся сигналам, так как (k+1) - ая производная этого сигнала по времени равна нулю
Гармонический
сигнал
не является медленно меняющимся, так
как ни одна из его производных не равна
нулю
Для определения динамической ошибки представим функцию We(p) рядом Тейлора
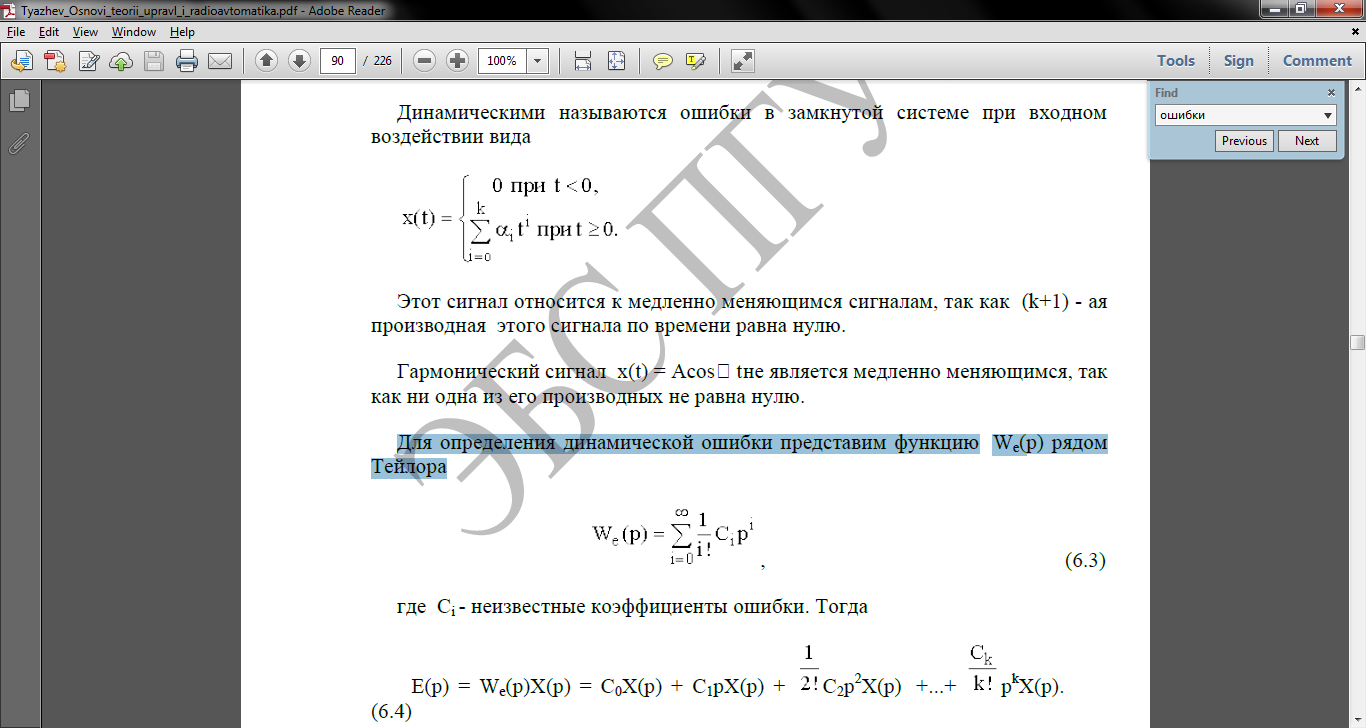
где Сi - неизвестные коэффициенты ошибки. Тогда
//
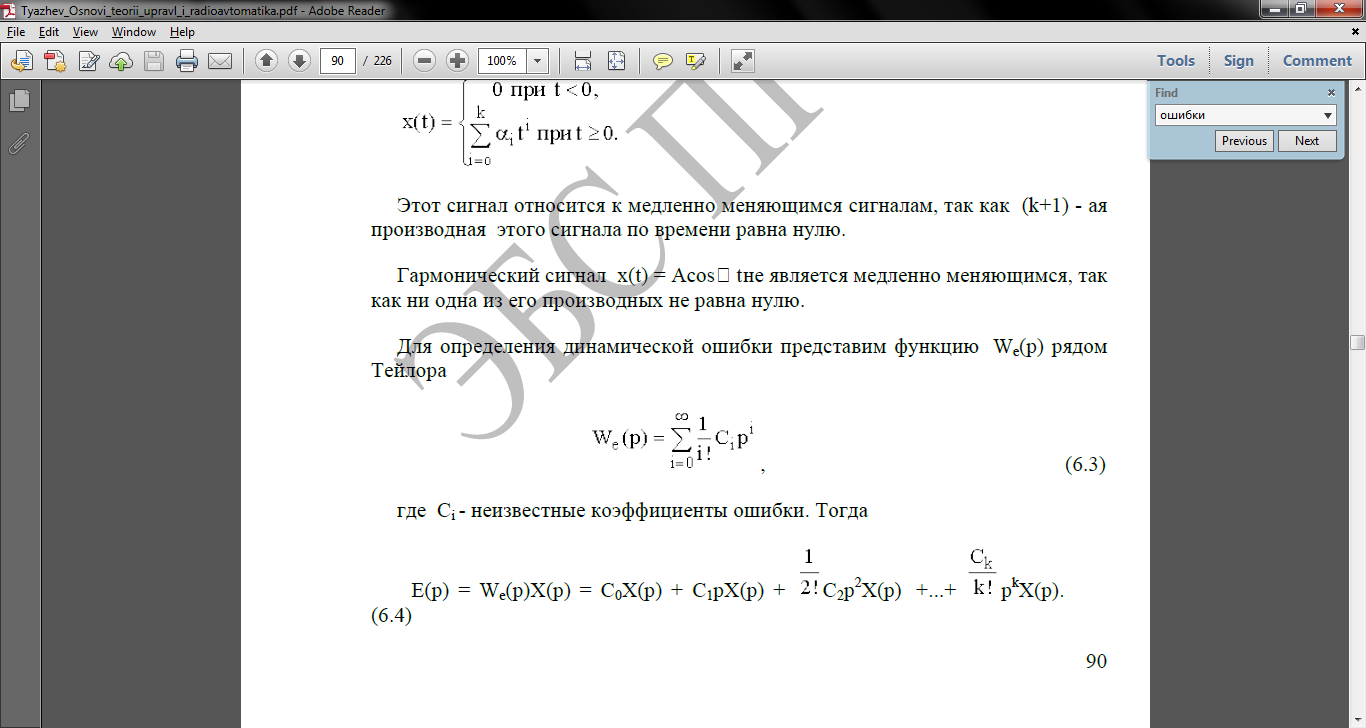
Этот ряд ограничен
k-тым членом ряда, так как
при
,
поэтому
при
.
Взяв от (6.4) обратное преобразование Лапласа, получим
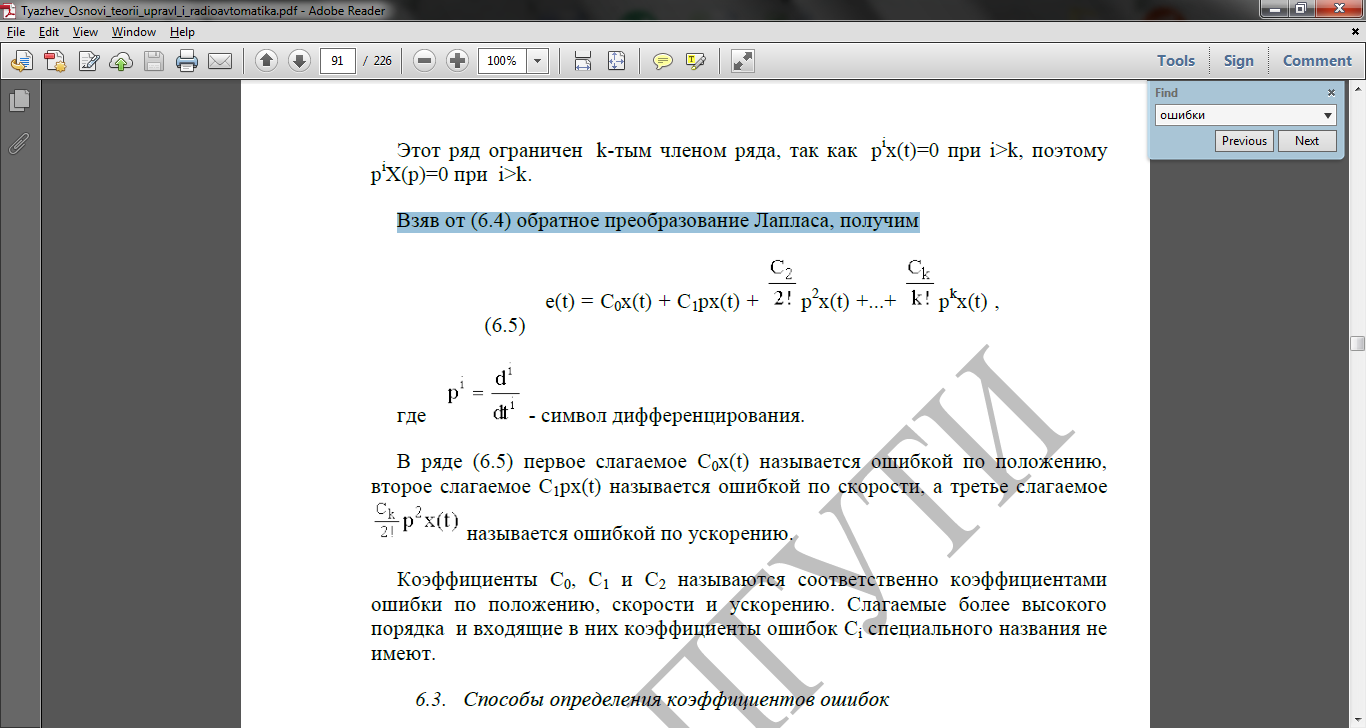
Где
- символ дефференцирования
В ряде (6.5) первое
слагаемое
называется
ошибкой по положению, второе слагаемое
называется
ошибкой по скорости, а третье слагаемое
называется
ошибкой по ускорению. Коэффициенты
C0,
C1 и
C2 называются
соответственно коэффициентами ошибки
по положению, скорости и ускорению.
Слагаемые более высокого порядка и
входящие в них коэффициенты ошибок Ci
cпециального названия не имеют.
Способы определения коэффициентов ошибок
Первый способ: коэффициенты ошибки Ci определяются по формуле
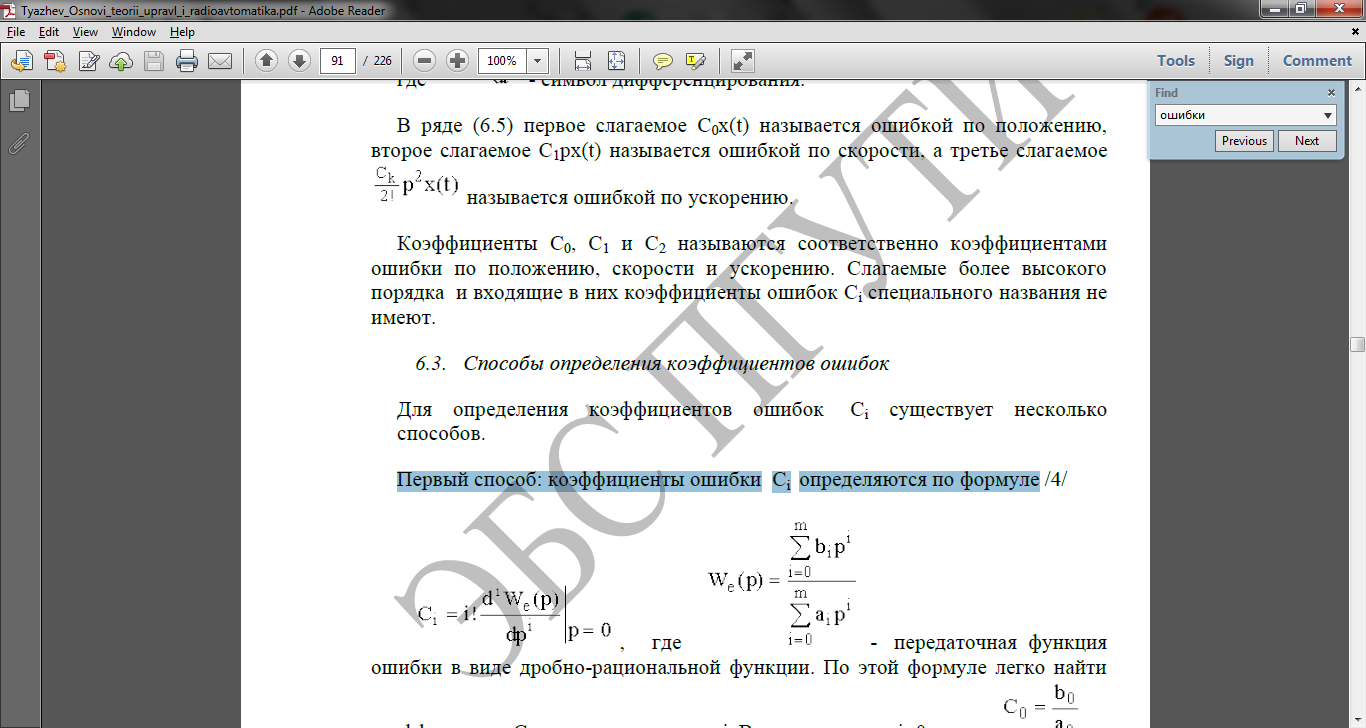- передаточная
функция ошибки в виде дробно-рациональной
функции. По этой формуле легко найти
коэффициенты
Ci для
малого индекса i. В частности для i=0 имеем
Второй способ.
Имеем два выражения передаточной функции ошибки в виде отношения полиномов:
и виде усеченного
ряда Тейлора
,
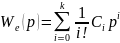следующего из
(6.3) с учетом (6.4). Приравняем правые части
этих выражений и получим
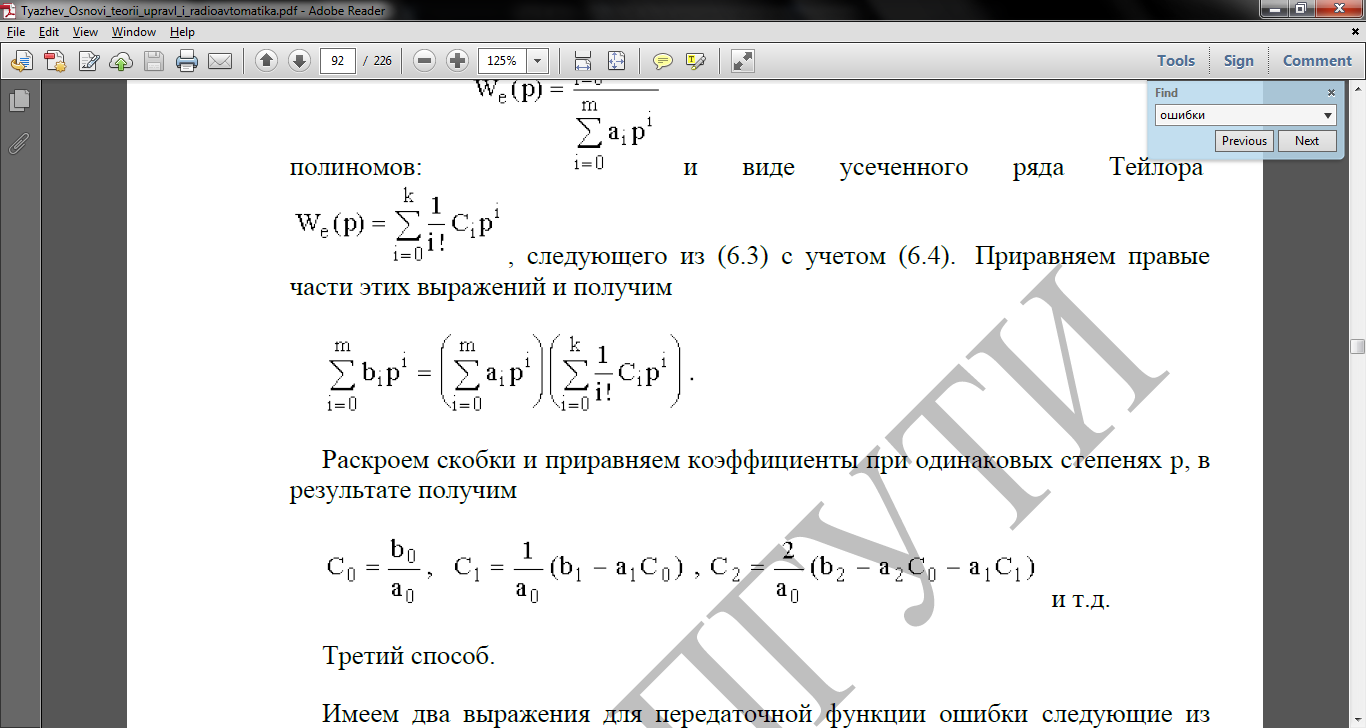
Раскроем скобки и приравняем коэффициенты при одинаковых степенях p, в результате получим
Третий способ.
Имеем
два выражения для передаточной функции
ошибки следующие из (6.2) и (6.3) с учетом
(6.4):
Представим
произведение
WpW0
в
виде
где K - коэффициент усиления замкнутой петли, ν - порядок астатизма, равный числу интеграторов в петле
Тогда
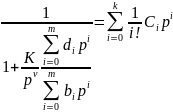
Далее как и во втором способе при различных порядках астатизма ν делаем операции с раскрытием скобок и приравниванием коэффициентов при равных степенях p .
В результате получим.
//пустой
квадрат это ν
//
При
,
,
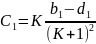и т.д
При
,
,
,
и т.д
При
,
,
,
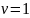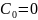и т.д
//
Из
этих выражений следует, что чем выше
порядок астатизма замкнутой системы,
тем больше коэффициентов системы равны
нулю. Но в замкнутых системах с
возникает проблема устойчивости