Создание пустого б-дерева

Чтобы построить дерево, сначала создается пустое дерево с помощью операции B_Tree_Create, а затем в него включаются элементы с помощью операции B_Tree_Insert. Обе эти операции используют вспомогательную операцию Allocate_Node, которая выделяет на диске место для нового узла. Эта операция занимает 0(1) времени и не использует операцию Disk_Read.

B_Tree_Create(T)

1. x <- Allocate_Node()

2. leaf [x] <- TRUE

3. n[x] <- 0

4. Disk_Write (x)

5. root[T] <- x

Операция требует 0(1) времени, т.к. выполняется одно обращение к диску.

Операция разбиения узла Б-дерева. Ключевым моментом добавления элемента в дерево является разбиение полного узла у с2t-1 ключами на два узла, имеющие по t-1 элементов в каждом. При этом ключ-медиана отправляется к родителю узла y - x. Этот ключ становится разделителем двух полученных узлов. Ключ-медиана вставляется в упорядоченное множество ключей узла х.

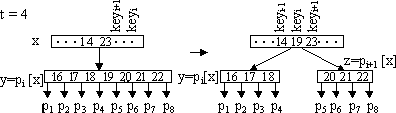
Элементы с большими, чем медиана ключами, переходят в новый узел z. Входными параметрами операции является неполный узел х, число i и полный узел y (y=p_i[x]).

B_Tree_Split (x, i, y)

1. z <- Allocate_Node()

2. leaf [z] <- leaf [y]

3. n[z] <- t-1

4. for j <- 1 to t-1

5.  dv key_j[z] <- key_j+1[y]

6. if not leaf [y]

7.  then for j <- 1 to t

8.   dv p_j[z] <- p_j+1[y]

9. n[y] <- t-1

10. for j <- n[x]+1 downto i+1

11.  dv p_j+1[x] <- p_j[x]

12. p_j+1[x] <- z

13. for j <- n[x] downto i

14.  dv key_j+1[x] <- key_j[x]

15. key_i[x] <- key_t[y]

16. n[x] <- n[x+1]

17. Disk_Write [x]

18. Disk_Write [y]

19. Disk_Write [z]

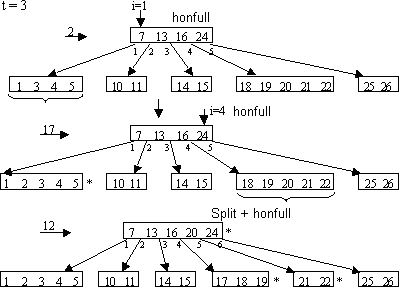
Добавление элемента в Б-дерево. Операции при включении проходит по одному из путей поиска от корня к месту. Для этого требуется время 0(th)=0(t log_tn) и 0(h) обращений к диску. На пути поиска встречающиеся полные узлы расщепляются с помощью операции B_Tree_Split.

Создание пустого б-дерева (продолжение)

B_Tree_Insert (T, k)

1. r <- root[T]

2. if n[r]=2t-1

3.  then

4. s <- Allocate_Node()

5.  root <- s

6.  leaf[s] <- FALSE

7.  n[s] <- 0

8.  p₁[s] <- 2

9.  B_Tree_Split (S, 1, r)

10.  B_Tree_Insert_Nonfull (s, k)

11. else B_Tree_Insert_Nonfull (r, k)

Точкой роста Б-дерева является не лист, а корень.

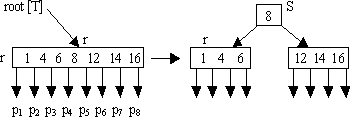
Новый корень содержит ключ-медиану старого корня.

Сделав корень неполным (или он не был таковым с самого начала), мы вызываем операцию B_Tree_Insert_Nonfull (x, k), которая добавляет элемент k в поддерево с корнем в неполном узле х. Это рекурсивная операция.

B_Tree_Insert_Nonfull (x, k)

1. i <- n[x]

2. if leaf[x]=TRUE

3.  then while i   1 and k < key_i[x]

4.   dv key_i+1[x] <- key_i[x]

5.    i <- i-1

6.   key_i+1[x] <- k (данные)

7.   n[x] <- n[x]+1

8.   Disk_Write [x]

9.  else while i   1 and k < key_i[x]

10.   dv i <- i-1

11.   i <- i+1

12.   Disk_Read (p_i[x])

13.   if n[p[x]]=2t-1

14.    then B_Tree_Split (x, i, p_i[x])

15.     if k > key_i[x]

16.      then i <- i+1

17.   B_Tree_ Insert_Nonfull (p_i[x], k)