Индексированные файлы (окончание)

Допустим, что есть отсортированный файл записей, хранящихся в блоках В1, В2, ..., Вх. Чтобы вставить в этот отсортированный файл новую запись, используется индексный файл, с помощью которого определяется, какой блок Вi должен содержать новую запись. Если новая запись умещается в блок Вi, она туда помещается в правильной последовательности. Если новая запись становится первой записью в блоке Вi, тогда выполняется корректировка индексного файла.

Если новая запись не умещается в блок Bi, то можно применить одну из нескольких стратегий. Простейшая из них заключается в том, чтобы перейти на блок Bi+1 (который можно найти с помощью индексного файла) и узнать, можно ли последнюю запись Bi переместить в начало Bi+1. Если можно, последняя запись перемещается в Bi+1, а новую запись можно затем вставить на подходящее место в Bi. В этом случае нужно скорректировать вход индексного файла для Bi+1 (и возможно для Bi).

Если блок Bi+1 так же заполнен или если Bi является последним блоком, то из файловой системы нужно получить новый блок. Новая запись вставляется в этот новый блок, который должен размещаться вслед за блоком Bi. Затем используется процедура вставки в индексном файле записи для нового блока.

Несортированные файлы с плотным индексом

Еще одним способом организации файла записей является сохранение произвольного порядка записей в файле и создание другого файла, с помощью которого будут отыскиваться требуемые записи; этот файл называется плотным индексом.

Плотный индекс состоит из пар (х, р), где р - указатель на запись с ключом х в основном файле. Эти пары отсортированы по значениям ключа. В результате структуру, подобную разреженному индексу (или В-дереву), можно использовать для поиска ключей в плотном индексе.

При использовании такой организации плотный индекс служит для поиска в основном файле записи с заданным ключом. Если требуется вставить новую запись, отыскивается последний блок основного файла и туда вставляется новая запись. Если последний блок полностью заполнен, то надо вставить новый блок из файловой системы. Одновременно вставляется указатель на соответствующую запись в файле плотного индекса. Чтобы удалить запись, в ней просто устанавливается бит удаления и удаляется соответствующий вход в плотном индексе (возможно, устанавливая и здесь бит удаления).

Внешние деревья поиска

Древовидные структуры данных можно использовать для представления внешних файлов. В-дерево (как и В+дерево) особенно удачно подходит для представления внешней памяти и стало стандартным способом организации индексов в системах баз данных.

Разветвленные деревья поиска

Обобщением дерева двоичного поиска является m-арное дерево, в котором каждый узел имеет не более m сыновей. Так же, как и для деревьев двоичного поиска, считается, что выполняется следующее условие: если n1 и n2 являются двумя сыновьями одного узла и n1 находится слева от n2, тогда все элементы, исходящие вниз от n1, оказываются меньше элементов, исходящих вниз от n2.

Однако в данном случае существует проблема хранения записей в файлах, когда файлы хранятся в виде блоков внешней памяти. Правильным применением идеи разветвленного дерева является представление об узлах как о физических блоках. Внутренний узел содержит указатели на свои m сыновей, а так же m-1 ключевых значений, которые разделяют потомков этих сыновей. Листья так же являются блоками; эти блоки содержат записи основного файла.

Использование m-арного дерева поиска значительно сокращает число обращений к блокам и время поиска записи по сравнению с деревом двоичного поиска, состоящего из n узлов.

Однако нельзя сделать m сколь угодно большим, поскольку, чем больше m, тем больше должен быть размер блока. Считывание и обработка более крупного блока занимает больше времени, поэтому существует оптимальное значение m, которое позволяет минимизировать время, требующееся для просмотра внешнего m-арного дерева поиска. На практике значение, близкое к такому минимуму, получается для довольно широкого диапазона величин m.

В+дерево

В+дерево - это особый вид сбалансированного m-арного дерева, который позволяет выполнять операции поиска, вставки и удаления записей из внешнего файла с гарантированной производительностью для самой неблагоприятной ситуации. С формальной точки зрения В+дерево порядка m представляет собой m-арное дерево поиска, характеризующееся следующими свойствами:

1. Корень либо является листом, либо имеет по крайней мере двух сыновей.

2. Каждый узел, за исключением корня и листьев, имеет от (m/2) до m сыновей.

3. Все пути от корня до любого листа имеют одинаковую длину.

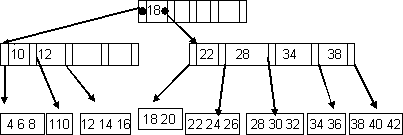
Рис.4. В+дерево порядка 5.

В+дерево можно рассматривать как иерархический индекс, каждый узел в котором занимает блок во внешней памяти. Корень В+дерева является индексом первого уровня. Каждый нелистовой узел на В+дереве имеет форму (p0, k1, p1, k2, p2, ..., kn, pn), где рi является указателем на i-го сына, 0   i   n, а ki - ключ, 1   i   n. Ключи в узле упорядочены, поэтому k1 < k2 < ... < kn. Все ключи в поддереве, на которые указывает р0, меньше, чем k1. В случае 1   i < n все ключи в поддереве, на которое указывает рi, имеют значения не меньше, чем, ki, и меньше, чем ki+1. Все ключи в поддереве, на которое указывает pn, имеют значения, не меньшие, чем kn.

Существует несколько способов организации листьев. В данном случае мы предполагаем, что записи основного файла хранятся только в листьях. Предполагается также, что каждый лист занимает один блок.

Поиск записей. Если требуется найти запись r со значением ключа х, нужно проследить путь от корня до листа, который содержит r, если эта запись вообще существует в файле. Путь проходится, последовательно считывая из внешней памяти в основную внутренние узлы (p0, k1, p1, .., kn, pn) и вычисляя положение х относительно ключей к1, к2, ..., кn. Если ki   x   ki+1, тогда в основную память считывается узел, на который указывает рi, и повторяется описанный процесс. Если х < к1, для считывания в основную память используется указатель р0; если х > kn, тогда используется рn. В результате этого процесса получаем какой-либо лист и пытаемся найти запись со значением ключа х. Если количество входов в узле невелико, то в этом случае можно использовать линейный поиск; в противном случае лучше воспользоваться двоичным поиском.

Вставка записей. Вставка в В+дерево подобно вставке в 2-3-дерево. Если требуется вставить в В+дерево запись r со значением ключа х, нужно сначала воспользоваться процедурой поиска, чтобы найти лист L, которому должна принадлежать запись r. Если в L есть место для этой записи, то она вставляется в L в требуемом порядке. В этом случае внесение каких-либо изменений в предков листа L не требуется.

В+дерево (окончание)

Если же в блоке листа L нет места для записи r, то у файловой системы запрашивается новый блок L1 и перемещается вторая половина записей из L в L1, вставляя r в требуемое место в L или L1. Допустим, узел Р является родителем узла L. Р известен, поскольку процедура поиска отследила от корня к листу L через узел Р. Теперь можно рекурсивно применить процедуру вставки, чтобы разместить в Р ключ к1 и указатель l1 на L1; к1 и l1 вставляются сразу же после ключа и указателя для листа L. Значение к1 является наименьшим значением ключа в L1.

Если Р уже имеет m указателей, вставка к1 и l1 в Р приведет к расщеплению Р и потребует вставки ключа и указателя в узел родителя Р. Эта вставка может произвести "эффект домино", распространяясь на предков узла L в направлении корня(вдоль пути, который уже был пройден процедурой поиска). Это может даже привести к тому, что понадобится расщепить корень (в этом случае создается новый корень, причем две половины старого корня выступают в роли двух его сыновей). Это единственная ситуация, при которой узел может иметь менее m/2 потомков.

Удаление записей. Если требуется удалить запись r со значением ключа х, нужно сначала найти лист L, содержащий запись r. Если такая запись существует, то она удаляется из L. Если r является первой записью в L, переходим после этого в узел Р (родитель листа L), чтобы установить новое значение первого ключа для L. Но если L является первым сыном узла Р, то первый ключ L не зафиксирован в Р, а появляется о одном из предков Р. Таким образом, надо распространить изменение в наименьшем значении ключа L в обратном направлении вдоль пути от L к корню.

Если блок листа L после удаления записи оказывается пустым, он отдается файловой системе. После этого корректируются ключи и указатели в Р, чтобы отразить факт удаления листа L. Если количество сыновей узла Р оказывается теперь меньшим, чем m/2, проверяется узелР1, расположенный в дереве на том же уровне слева(или справа) от Р. Если узел Р1 имеет по крайней мере (m/2)+2 сыновей, ключи и указатели распределяются поровну между Р и Р1 так, чтобы оба эти узла имели по меньшей мере (m/2) потомков сохраняя упорядочение записей. Затем надо изменить значения Р и Р1 в родителе Р и, если необходимо, рекурсивно распространить воздействие внесенного изменения на всех предков узла Р, на которых это изменение отразилось.

Если у Р1 имеется ровно (m/2) сыновей, то нужно объединить Р и Р1 в один узел с 2(m/2)-1 сыновьями. Затем необходимо удалить ключ и указатель на Р1 из родителя на Р1. Это удаление можно выполнить с помощью рекурсивного применения процедуры удаления.

Если "обратная волна" воздействия удаления докатывается до самого корня, то возможно придется объединить только двух сыновей корня. В этом случае новым корнем становится результирующий объединенный узел, а старый корень можно вернуть файловой системе. Высота В+дерева уменьшается на единицу.

В-деревья

Б-деревья - сбалансированные деревья, удобные для хранения информации на дисках. Характерным для Б-деревьев является их малая высота h. Представление информации во внешней памяти в виде Б-дерева стало стандартным способом в системах баз данных.

Пример: Б-дерево степени 5:

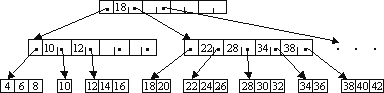
В Б-дереве узел может иметь много сыновей, на практике до тысячи. Количество сыновей (максимальное) определяет степень Б-дерева.

Узел х, хранящий n[x] ключей, имеет n[x]+1 сыновей. Хранящиеся в х ключи служат границами, разделяющими всех потомков узла на n[x]+1 групп. За каждую группу отвечает один из сыновей х. При поиске в Б-дереве искомый ключ сравнивается с границами в узле х и выбирает один из n[x]+1 путей для дальнейшего поиска.

Особенности структуры Б-дерева вытекают из особенностей обработки информации во внешней памяти. Обычно эта информация (множество) имеет весьма большой объем и насчитывает миллионы и миллиарды элементов. Хранить такой объем в ОП невозможно. При обработке в ОП хранится только часть элементов, обрабатываемых в данный момент.

Общая схема обработки отдельных элементов выглядит так:

1. ...

2. x <- указатель на какой-либо объект

3. Disk_Read(x)

4. обработка и изменение элемента х

5. Disk_Wirte(x)

6. операции, которые только используют элемент х, но не изменяют его

7. ...

Особенность операций считывания и записи на диск является то, что:

1) время доступа к области на диске, содержащей элемент х, значительно больше, чем к ячейке ОП (до 20 миллисекунд);

2) одно чтение/запись считывает или записывает сектор дорожки магнитного диска размером в несколько килобайт.

Т.е. вместе с элементом х считываются/записываются и смежные элементы. Поэтому узлы Б-дерева содержат не один элемент, а группу элементов размером в 1 сектор. Чтобы уменьшить количество операций чтения-записи на диск при поиске элемента в Б-дереве, нужно максимально уменьшить его высоту. Для этого степень Б-дерева делается максимальной. Типичная степень - (50-2000). Она зависит от соотношения размера сектора и размера отдельного элемента. Например, Б-дерево степени 1000 и высоты 2 может хранить более миллиарда ключей.

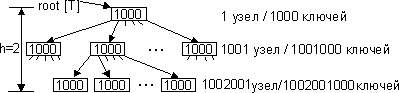
Узел-корень дерева обычно всегда хранится в ОП, для доступа к остальным ключам требуется всего 2 операции чтения с диска.

В-деревья (продолжение)

Представление Б-дерева. Как и в других деревьях, дополнительная информация и ключи хранятся в узлах дерева. Обычно дополнительная информация представлена в виде ссылки на сектор диска, где она хранится. Вместе с ключом при его перемещении дополнительная информация перемещается вместе с ним.

В отличие от 2-3 дерева ключи и дополнительная информация размещается не только в листьях, но и во внутренних узлах дерева. Хотя возможна организация Б-деревьев, в которых дополнительная информация хранится только в листьях, а во внутренних узлах - ключи и указатели на сыновей. Это экономит память во внутренних узлах и позволяет увеличить их степень при том же размере сектора.

Кроме того, узел хранит:

1) n[x] - текущее количество ключей, хранящихся в узле;

2) сами ключи в неубывающем порядке key₁[x]   key₂[x]   ...   key_n[x][x];

3) булевский признак leaf[x], истинный, если узел - лист;

4) n[x]+1 указателей p₁[x], p₂[x], ..., p_n[x]+1[x] на сыновей. У листьев эти поля не определены.

Ключи key₁[x], ..., key_n[x][x] служат границами, разделяющими значения ключей в поддеревьях:

K₁   key₁[x]   key₂[x]   ...   key_n[x][x]   K_n[x]+1,

где K_i - множество ключей, хранящихся в поддереве с корнем p_i[x].

Все листья находятся на одной глубине, равной высоте дерева h.

Число ключей, хранящихся в одном узле, ограничено сверху и снизу единым для Б-дерева числом t, где t - минимальная степень дерева (t   2).

Каждый узел, кроме корня содержит минимум t-1 ключей и t сыновей. Если дерево не пусто, то в корне должен храниться хотя бы один ключ. В узле хранится не более 2t-1 ключ, и внутренний узел имеет не более 2t сыновей. Узел, хранящий 2t-1 ключей, называется полным.

Если t=2, то у каждого внутреннего узла может быть 2, 3, 4 сына и такое дерево называется 2-3-4 деревом.

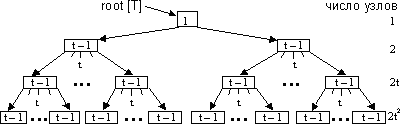
Высота дерева:

Минимальное:

Т.е. временная сложность операций для Б-дерева оценивается как 0(log_tn).

.

Операции для Б-дерева (особенности). Считаем, что корень дерева всегда находится в ОП и операция Disk_Read для корня не выполняется. Но когда корень изменяется, его нужно сохранять на диске. Все узлы, передаваемые операциям, как входные параметры, уже считаны с диска.

В-деревья (окончание)

Поиск в Б-дереве. Рассмотрим рекурсивную операцию B_Tree_Search, параметрами которой является указатель х на корень поддерева и ключ k искомого элемента. Операция вызывается первоначально для корня дерева B_Tree_Search(root[T], k). При нахождении в дереве элемента с заданным ключом операция возвращает пару (y, i), где у - узел Б-дерева, i - порядковый номер указателя, для которого key_i[y]=k. Иначе операция возвращает nil.

B_Tree_Search(x, k)

1. i <- 1

2. while i   n[x] and k > key_i[x]

3.  dv i <- i+1

4. if i   n[x] and k=key_i[x]

5.  then return (x, i)

6. if leaf [x]

7.  then return nil

8.  else Disk_Read (p_i[x])

9.   return B_Tree_Search (p_i[x], k)

При проходе по Б-дереву число обращений к диску 0(h). Цикл while занимает основное время вычислений и занимает время 0(th).