Глава 6. Корреляция параметров затвердевания и стабильности структуры с приведенной температурой и с мерой квантовости.

6.1. ОСНОВНАЯ ЗАКОНОМЕРНОСТЬ ИНТЕРВАЛА ЗАТВЕРДЕВАНИЯ, Е ~ Т^-n.

6.1.1. ЗАВИСИМОСТЬ ЭНЕРГИИ АКТИВАЦИИ ОТ ТЕМПЕРАТУРЫ В ТРАДИЦИННОЙ И В ПРЕДЛАГАЕМОЙ МОЛЕКУЛЯРНОЙ МОДЕЛИ ВЕЩЕСТВА. КОНСТАНТЫ, ОБУСЛОВЛЕННЫЕ ОБЫЧНЫМИ ВЗАИМОДЕЙСТВИЯМИ И СТАБИЛИЗИРУЮЩИМИ СТРУКТУРУ ЭФФЕКТАМИ.

Как известно, понятие об энергии активации сформировалось первоначально в теории скорости химических реакций. Аррениус показал, что скорость реакции V зависит от температуры по уравнению lnV = A - B/T или lnV = A - E/RT. В теории Эйринга такая зависимость объясняется тем, что при перегруппировке атомов, соответствующей элементарному акту реакции , комплекс проходит через "активированное" состояние, или преодолевает энергетический барьер высотою Е; равновесная концентрация активированных комплексов в соответствии с распределением Больцмана пропорциональна exp(-E/RT). Позднее было замечено, что вязкость или коэффициент самодиффузии также зависят от температуры по экспоненте [77], и следовательно, процессы переноса также принадлежат к активационным процессам, в элементарном акте которых преодолевается энергетический барьер высотою ЕV, ЕD. В период распространения, "популярности" квазикристаллических концепций жидкости, существовала тенденция определять энергии активации даже у простых жидкостей, например, у высокотемпературных металлических расплавов [30]; существование этих энергетических барьеров считалось очевидным. Энергии Е определяли обычно по тангенсу угла наклона корреляции ln - 1/T, то есть в полулогарифмических координатах. И сейчас иногда определяют Е, которые оказываются меньше RT. Конечно, это не физические, а лишь формальные "энергии активации"; такая же обработка данных по разреженным газам формально дала бы ЕD = 3/2RT, EV = 1/2RT, хотя, конечно, диффузия или течение в газе идут без преодоления каких-либо энергетических барьеров.

В настоящее время квазикристаллические концепции несколько потеснены и, соответственно, имеется обратная тенденция строить теорию кинетических свойств реальных жидкостей и даже твёрдых тел без энергетических барьеров и без энергий активации, например, на базе модели жёстких сфер [51, 77]; в таких теориях перегруппировки атомов затруднены лишь чисто кинетическими причинами. Однако для последовательного описания широкого опытного материала практически невозможно обойтись без представления об активированных элементарных актах процессов переноса.

Согласно традиционным представлениям, энергии активации Е должны быть почти постоянными, почти независящими от температуры, как и энергия связи. Действительно, величина Е расходуется на разрыв части связей и определяется разностью энергии связи в активированном Uа и исходном Uо состояниях; Е=Uо-Uа. Производная dE/dT=C=Cа- Cо равна разности теплоёмкостей в активированном и исходном состояниях; теплоёмкости имеют величину около 3R, и, следовательно, их разность также должна быть величиною порядка не более R, ABS(dE/dT)  R. Так как энергии активации диффузии или вязкости часто составляют 100 - 1000 кДж/моль, то они должны изменяться не больше, чем приблизительно на 1/10000 на градус, то есть должны оставаться практически постоянными; так ведут себя обычно теплоты испарения или тепловые эффекты реакций.

Согласно предлагаемой модели, стабильность структуры и характеризующие её величины энергий активации обусловлены квантовыми эффектами и при охлаждении должны возрастать соответственно росту квантового параметра. Это подтверждается основной закономерностью интервала затвердевания - ростом энергий активации пропорционально Т^-n, например, примерно в 30 раз от температуры Тп перехода в состояние реальной жидкости до точки стеклования, Тст, и от ЕV  RTпл при Т = Тп до Е  30RTпл при Т = Тст.

Первые данные об интенсивном изменении энергий активации с температурой были получены давно [81, 30], когда вязкость стёкол и аналогичных низкотемпературных жидкостей была изучена в широком интервале в несколько порядков величины. Выяснилось, что зависимость ln- 1/T не остаётся линейной, но закономерно искривляется; её считали линейной, а её угловой коэффициент - энергию активации - считали постоянным лишь потому, что искривление незаметно в узких интервалах, изученных ранее. Для температурной зависимости Е в изученных стёклах был предложен ряд уравнений [81, 30]. Мы описываем эту зависимость формулой Е ~ Т^-n, у стёкол n 2. Последующий анализ опытных данных с позиций предлагаемой модели привел к выводу, что подобное нарастание энергий активации и жесткости структуры при охлаждении - общая закономерность, характерная не для некоторых стёкол, но практически для всех веществ [7]. Выяснилось, что приблизительно так же нарастает энергия активации вязкости при охлаждении у всех жидкостей, в том числе и у маловязких жидкостей в той области несколько ниже Тп, где отклонения от модели простой жидкости ещё невелики и вязкость мала; примерно так же нарастают при охлаждении величины ЕV, ЕD, даже у кристаллических веществ около температуры плавления.

Зависимость ЕV ~ Т^-n удобно выявлять, располагая опытные данные в координатах (dln/dlnT - ln) - ln. На таком графике получается линейная зависимость с угловым коэффициентом, равным n. Широко использовали также более простые координаты (dln/dlnT - ln) и ( dln/dlnT - T).

Можно выделить две группы процессов и, соответственно, два типа констант скорости и равновесия различных процессов:

а) константы, связанные с обычными взаимодействиями; их энергия активации (или теплота H) почти не зависит от температуры.

б) константы, связанные со стабилизирующими эффектами; энергии активации интенсивно зависят от температуры, Е ~ Т^-n.

К первым можно отнести, например, давления паров жидкостей или твёрдых тел, константы скоростей испарения, константы равновесия диссоциации прочных газовых молекул и константы скорости этих процессов. Примером констант, связанных со стабилизирующими эффектами, с жёсткостью структуры, могут служить обсуждаемые коэффициенты вязкости, диффузии, ионной электропроводности в интервале затвердевания.

Уже выработался [7] ряд способов выяснения - является ли данная константа k обычной или связана со стабилизирующими эффектами, тоесть относится ли к группе а) или б);

1) Первый способ состоит в том, что опытные данные представляют в координатах (dlnk/dlnT - lnk) - lnk. На таком графике обычные константы дают практически горизонталь, а вязкость реальной жидкости - наклонную прямую с большим угловым коэффициентом 1 - 5, равным показателю n уравнения Е ~ Т^-n. Рост Е, тоесть жесткости структуры, при охлаждении отражает затвердевание.

2) В привычных полулогарифмических координатах lnk - 1/T обычные константы дают практически линейную зависимость, а коэффициенты вязкости, диффузии и др. - искривлённую, см. рисунок 6.1. Однако различить "на глаз" две группы констант в этих координатах труднее; как обычно, характер экспериментальной зависимости легче определяется в тех координатах, где данная зависимость "спрямляется", близка к прямой.

3) Еще одно отличие процессов и констант а) и б) выявляется по величине предэкспоненциального множителя kо. Экстраполяция зависимости lnk - 1/Т до оси ординат ( до 1/Т = 0 ) даёт, как известно, предэкспоненциальный множитель kо зависимостей k = kоexp(E/RT). У обычных констант предэкспоненциальный множитель имеет "нормальную" величину, равную константе скорости или равновесия процесса в такой же системе, но без энергетических барьеров, при Е = 0; например, случае коэффициентам вязкости или диффузии в простой жидкости. У констант группы б), определяемых стабилизирующими структуру эффектами, предэкспоненциальный множитель вследствие искривления графика lnk - 1/Т получается переменным и завышенным, например, на 5 - 10 порядков величины. По этой причине теория предэкспоненциального множителя часто оказывается "самой сложной частью теории диффузии"[200] или вязкости.

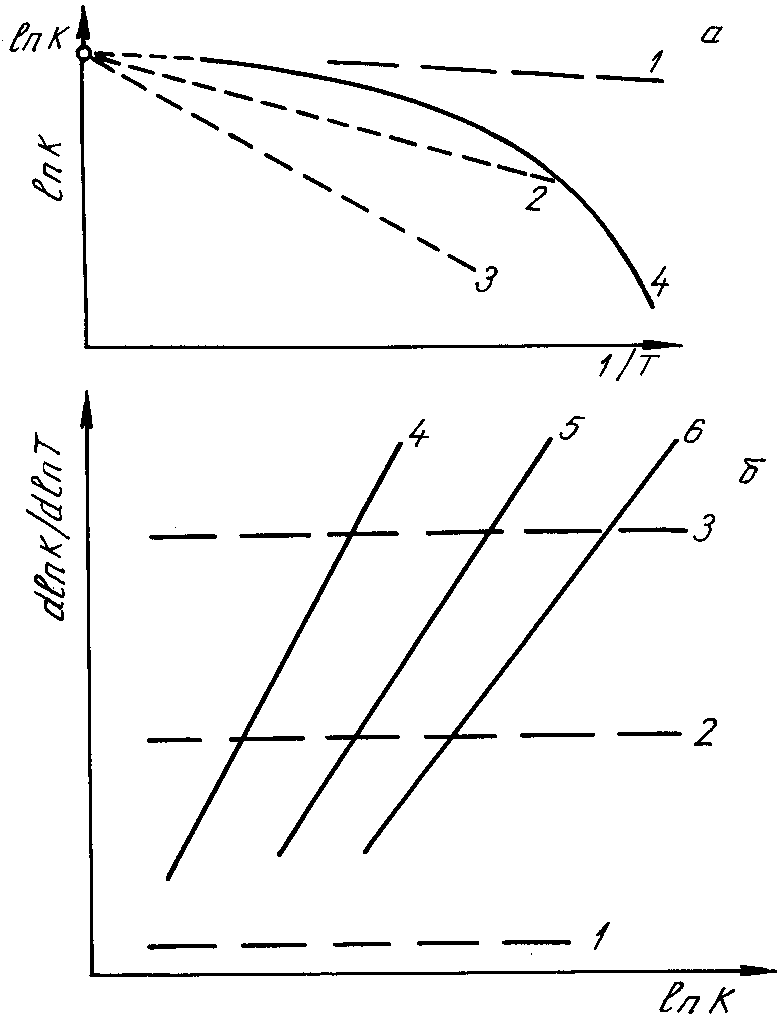
Рис.6.1 Вид политерм в случае костант, связанных с обычными химическими взаимодействиями (1, 2, 3) и констант, обусловленных стабилизирующими структуру эффектами (4, 5, 6) в дифференциальных (б) и обычных полулогарифмических координатах (а).

4) Кроме того, обычные константы дают весьма слабые компенсационные эффекты (КЭФ) со степенью компенсации в несколько процентов, тогда как у коэффициентов вязкости, диффузии реальной жидкости степень компенсации КЭФ приближается к 100% ([7], подробнее см. ниже).

По этим признакам или их совокупности нетрудно выяснить, определяется ли рассматривемый процесс обычными взаимодействиями или стабилизирующими структуру эффектами, если имеется достаточно длинная температурная зависимость константы данного процесса, определённая с не слишком большими ошибками.

Все перечисленные особенности констант, связанных с жесткостью структуры, отражают интенсивную зависимость этой жесткости и энергий активации от температуры; в сущности, они выражают затвердевание. Почти горизонтальные политермы обычных констант свидетельствуют о слабой зависимости энергии связи от температуры.

Эти особенности кинетических коэффициентов (и всех констант группы б )) не поддаются объяснению в рамках традиционной молекулярной модели вещества, по крайней мере, при обычных представлениях о механизме процессов переноса. В частности, при традиционном рассмотрении расчётные величины теплоёмкости Са активированных частиц получаются нефизическими; например, расчёт Са по формуле Са = С+С = С+dE/dT = C+ d/dT(RT*dlnk/dT) несколько выше точки стеклования даёт аномальные, например, завышенные на порядок величины, и к тому же отрицательные значения теплоёмкости Са активированного атома, например Са= - 30R. Однако данное противоречие традиционной модели и опытных данных в основном оставалось незамеченным и не вызвало, насколько нам известно, больших дискуссий, таких, как дискуссии по "фазовым переходам" в расплавах или по микрорасслоению эвтектик. Вместе с тем аномальные значения расчётных теплоёмкостей ещё в 50-е годы были одним из основных аргументов теоретиков при "опровержении" особенностей на политермах, найденных Кочневым И.М. (см. параграф 3.1.)

6.1.2.КОРРЕЛЯЦИИ, ВЫРАЖАЮЩИЕ ЗАВИСИМОСТЬ Е ~ Т^-n.

Динамику затвердевания, тоесть нарастания жесткости структуры и выражающих её энергий активации, удобно начать анализировать по опытным данным для вязкости: во-первых, они более показательны, потому что вязкость изменяется при затвердевании более интенсивно по сравнению с другими кинетическими коэффициентами; во-вторых, данные по вязкости более многочисленны. Другие кинетические коэффициенты рассмотрены здесь ниже. Коэффициенты диффузии, ионной электропроводности и др. изменяются качественно так же, как и вязкость; изменения всех кинетических свойств отражают нарастание общей жесткости структуры при охлаждении.

Рассмотрели и представили в координатах dln/dlnT - ln данные по вязкости нескольких сотен веществ. Были рассмотрены практически все достаточно длинные политермы вязкости, данные для которых нашлись в доступных справочниках, особенно в [9,10], а также в ряде обзоров и оригинальных работ. Проанализировали политермы более 100 оксидных, в основном, силикатных систем ([10] и др.); для многих таких расплавов изменение вязкости прослеживается на интервале до 10 порядков величины вязкости и более. Политермы жидких металлов и сплавов часто довольно короткие, но известны точки стеклования, где =10¹² Па*с. Это позволяет уверенно судить об общем виде политермы, так как известно, в какую точку она "приходит" после увеличения вязкости, например, на 15 порядков величины.

По данным для предельных углеводородов, от 1-го (CH₄) до 64-го (C₆₄H₁₃₀) хорошо прослеживается влияние размера молекулы на положение прямой dln/dlnT - ln. Рассматривали также неорганические жидкости, сжиженные газы, солевые расплавы, полимеры и их растворы и др. Некоторые данные приведены на рисунках 6.2, 6.3, 6.4, 6.5. Здесь даны приведённые значения вязкости 1 =/рг, где рг вязкость разреженного газа. На таком графике при достаточном перегреве каждая политерма "приходит" в начало координат, соответствующее состоянию разреженного газа. Точки перегретой простой жидкости располагаются недалеко от начала координат.

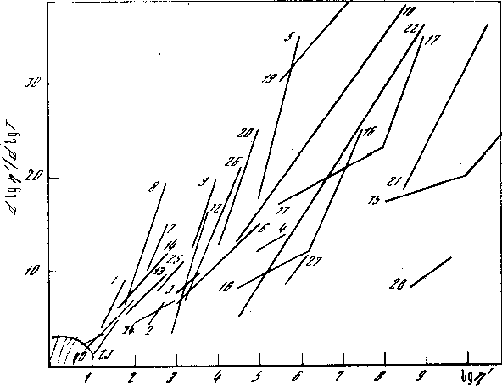
Рис. 6.2 Политермы вязкости жидкостей различной природы в дифференциальных координатах. 1, 2, 3, 4, 5, 6 - 16 непредельные углеводороды, 17 - 24 полимеры и их растворы.

Все жидкости дают наклонные прямые; средний угловой коэффициент составляет около трёх: tg = n+1  3, что соответствует зависимости Е ~Т^-2. Энергии активации вязкости Е, а значит, и стабильность, жёсткость структуры жидкости, интенсивно нарастают при охлаждении. Если бы энергии активации Е почти не зависели от температуры, как это считается обычно при традиционном подходе, то в обсуждаемых координатах dln/lnT-ln получились бы почти горизонтальные

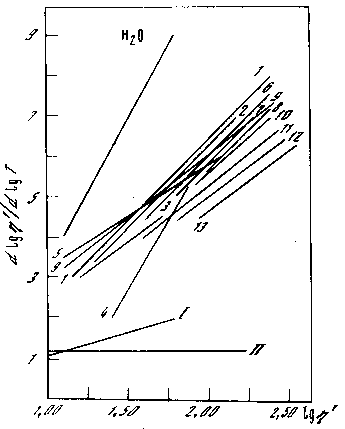
Рис. 6.3 Политермы воды и предельных углеводородов до (13).

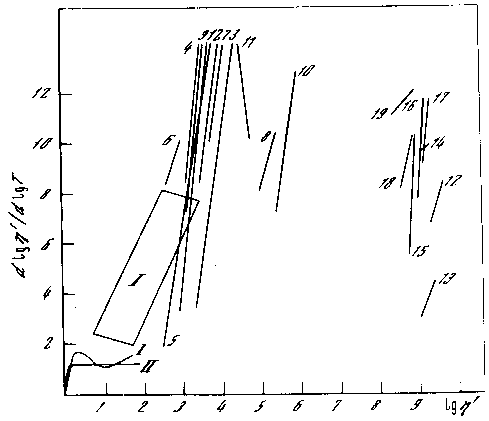
Рис. 6.4 Политермы вязкости растворов полимеров, смол , битумов (1-11). (12-19)- полиэтилен различных марок. Для сравнения нанесена область 1 воды и предельных углеводородов.

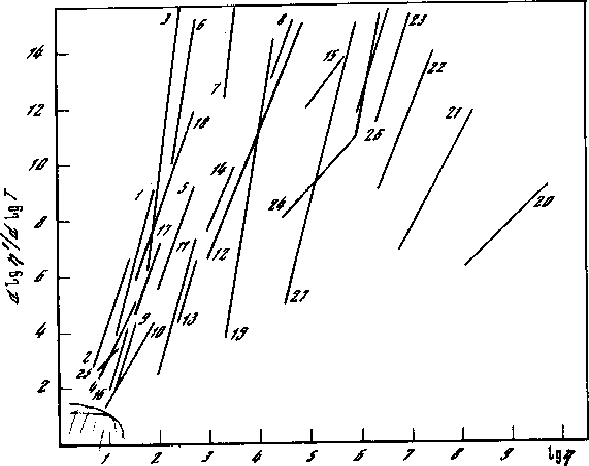
Рис.6.5 Политермы оксидов, солей и жидких металлов, стеклообразующих окислов. В этих координатах политермы высоко - и низкотемпературных жидкостей

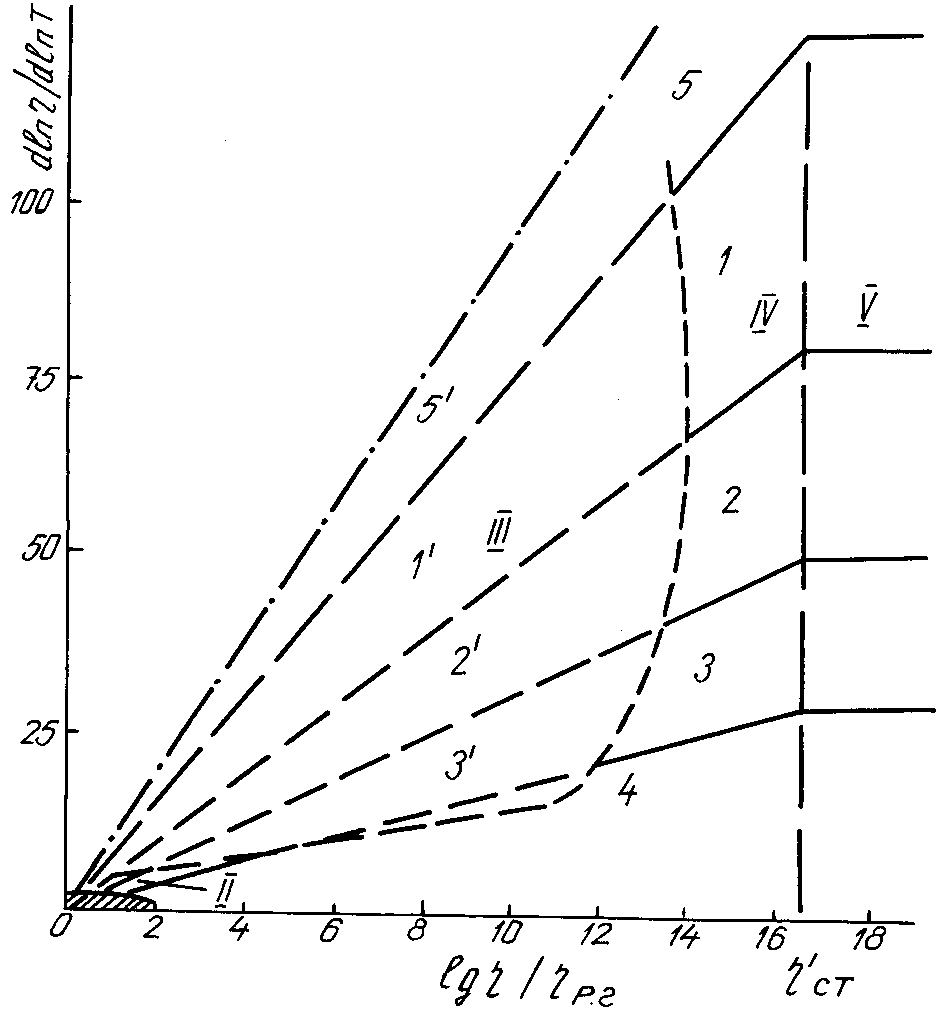
Рис.6.6 Схема расположения политерм основных групп вещества в дифференциальных координатах. 1,11 - молекулярные жидкости и кристаллы; 2,21 - жидкие и твёрдые металлы; 3,31 - оксидные расплавы; 4 - стеклообразующие окислы, полимеры; 5 - быстрозатвердевающие жидкости с крупными молекулами типа глюкозы. Штриховой кривой выделена область метастабильных состояний между жидкостью и кристаллом.

Обсуждаемые прямые на графике 6.6. исходят из области около начала координат, соответствующей газам и простым жидкостям, и доходят до линии "а" точек стеклования Тст, рисунок 6.6, на которой lg/рг  17. Далее располагается уже область твёрдого состояния. Значительные участки многих политерм приходятся на область термодинамически неустойчивых состояний между жидкостью и твёрдым телом, где опытных данных мало, но о ходе политерм можно судить по имеющимся данным выше и ниже этой области.

Экстраполяцией высокотемпературного жидкостного участка часто удаётся с удовлетворительной точностью определить температуру стеклования и другие точки низкотемпературной ветви политермы вязкости, поэтому нет оснований считать, что политерма идёт как-то иначе в средних, неизученных в настоящее время участках.

На некоторых политермах выявляются аномальные участки в виде минимумов или изломов, а также осцилляций и др. Вследствие таких аномалий экстраполяция некоторых прямых на рис. 6.2 - 6.5 приводит в область, довольно далёкую от начала координат. Это показывает, что на неизученных участках имеются искривления или какие-то другие особенности, благодаря которым политерма всё же приходит к состоянию простой жидкости около начала координат.

Различие угловых коэффициентов политерм вязкости на рис. 6.2 - 6.6 свидетельствует о том, что различным жидкостям присущ разный темп затвердевания, нарастания стабильности и жёсткости структуры при охлаждении. Самые крутые политермы (tg6) дают молекулярные жидкости с большими молекулами. Наличие жёсткой структуры внутри молекул способствует, видимо, быстрому нарастанию жёсткости и межмолекулярной структуры. Наименьший угловой коэффициент ( 2) имеют политермы вязкости стеклообразующих окислов (SiO₂, B₂O₃ и др.), а также полимеров; они отличаются от молекулярных веществ тем, что жесткость структуры и энергии активации по внутри- и межкомплексным связям близки.

Приведём некоторые числовые значения параметров интервала затвердевания. Для повышения вязкости B₂O₃ от 10^-2 до 10⁺¹¹ Па*c требуется понижение абсолютной температуры Т в 5,3 раза, а для такого же повышения вязкости глюкозы достаточно понижения температуры Т всего в 1,4 раза (от 140^оС до 22^оС). Стеклообразующий оксид B₂O₃ даёт весьма медленное затвердевание (tg2), а глюкоза, как молекулярная жидкость, быстрое (tg5).

Зависимость Е ~ Т^-n или Е = Е₀Т^-n приводит к изменению вязкости с температурой по уравнению: пр=exp(E₀T^-n/RT) (6.1)

Здесь пр - вязкость простой жидкости. Дифференцируя (6.1) по температуре, получаем уравнение линейных зависимостей, представленных на рис. 6.2 - 6.6:

В точке стеклования =10⁺¹² Па*с, и величина ln/пр в формуле (6.1) равна примерно 15*2,3 = 35; около температуры перехода Тп можно принять ln/пр = 1. Получается, следовательно, ln пр = (T/Tп)ⁿ⁺¹ (6.2)

При самом медленном затвердевании, при n = 1, интервал затвердевания от Тп до Тст займёт примерно 6-кратное изменение температуры: при Тп/Тст  6 и (n+1) = 2 выполняется условие (6.2). При среднем значении n = 2 Тп/Тст  3,2, а при быстром затвердевании, когда n = 5, Тп/Тст  1,8. В действительности у воды этот интервал занимает изменение температуры от 470 К до 138 К то есть в 3,4 раза, а у жидкого железа - от 1900 К до 900 К, то есть в 2,1 раза, и т.д.

Изменение энтропии взаимодействия Sвз в интервале затвердевания получается обычно от R до 3R, то есть примерно столько же, или несколько больше, чем при кристаллизации. По этому параметру непрерывное затвердевание от Тп до Тст термодинамически эквивалентно кристаллизации, или несколько больше ее.

Приведём ещё результаты определения точек стеклования Тст ряда молекулярных жидкостей экстраполяцией политермы вязкости по формуле (6.1):

Т, К	Вода	Дихлор	Пиридин	Тиофен	Ацетон	Этан
По формуле (6.1)	135	140	93	110	93	84
Опытные д., [66]	138	125	90	106	87	79

Видно, что такая экстраполяция примерно на 15 порядков величины по вязкости даёт удовлетворительные результаты.

Если рассматривать вязкость как функцию не температуры, а степени квантовости, то есть энтропии, = f (S), то с удовлетворительной точностью вычисляется обычно также и скачок вязкости при кристаллизации [7]. Удовлетворительные результаты таких расчетов и экстраполяций свидетельствуют о достаточной точности и общности найденных уравнений, в частности, E ~ T^-n.

Таким образом, анализ обширного экспериментального материала приводит к выводу, что в найденные уравнения и простые линейные графики рис. 6.2 - 6.6 с определённой точностью укладываются имеющиеся ([9, 10] и др.) данные по вязкости практически всех основных типов реальных жидкостей, (не считая областей аномалий), и даже данные ряда твёрдых стёкол около точки стеклования и кристаллических веществ около температуры плавления. Все рассмотренные жидкости имеют широкий интервал температур, от состояния простой жидкости до точки стеклования (до состояния твердого стекла), в котором жесткость структуры и отражающие её энергии активации нарастают при охлаждении пропорционально T^-n, от практически нулевой жёсткости простой жидкости до высокой и не изменяющейся далее жесткости структуры твердого тела; вполне естественно называть этот интервал температур интервалом затвердевания. Применялся также термин "интервал реальной или затвердевающей жидкости". Если допустить кристаллизацию, то часть данного интервала проходится скачком, "свёртывается" в точку кристаллизации. Затвердеванием в настоящее время часто называют другой процесс - изотермическую кристаллизацию; во избежание недоразумений нужно разграничивать такие применения терминов.

Выше обсуждаемого интервала затвердевания лежит область простой жидкости с практически нулевой жесткостью структуры, Е = 0. Ниже по температуре располагается область твердого состояния с высокой и практически постоянной жесткостью структуры (ЕV  30RTпл  const). Имеются, следовательно, переходы от простой жидкости к реальной и от реальной жидкости к твердому телу; эти превращения соответствуют началу и концу интервала затвердевания.