5. 3. 6. Уточнение формулы для поверхностного натяжения чистых жидкостей

Определяя потенциал взаимодействия жидкости вз по давлению паров, вз = RTln(RT/pVж), получаем из формулы (5.11):

 = *RTln(RT/pVж)/No^1/3Vж^2/3 . (5.13)

По этой формуле, а также по аналогичному уравнению, выражающему натяжение  через Fвз, было рассчитано поверхностное натяжение 160 жидкостей различной природы. Удовлетворительное согласие получается для молекулярных жидкостей от температуры плавления до околокритической области; для жидких металлов и полупроводников, окислов, стеклообразующих соединений со смешанным ионно-ковалентным взаимодействием и др. Ошибка расчета в большинстве случаев не превысила 5%. Расчет температурного коэффициента d/dT в результате замены Uвз на вз уточняется еще в большей степени, чем расчет самого натяжения. Политерма натяжения принимает вид, близкий к экспериментальной, за исключением околокритической области [179].

Формула (5.13), опубликованная в 1963 году [185 ], получила многочисленные отклики и применялась затем многими исследователями. Просьбы выслать оттиски работы поступили из 10 исследовательских центров Европы и Америки. Американские исследователи Гольд и Огле [186] проверили применимость предложенной формулы для еще 800 других жидкостей и сочли её одной из более точных; она вошла в справочник [187] в числе “наиболее достоверных методов расчета” поверхностного натяжения. Подобное уточнение формул для поверхностного натяжения в рамках традиционной молекулярной модели вещества было близко, очевидно, к направлению поисков многих исследователей. Более сложные последующие работы, выходящие за рамки традиционной модели и опровергающие ее в некоторых пунктах, обычно не получали откликов или же получали резко отрицательные отзывы.

5.3.7.Поверхностное натяжение растворов

С помощью потенциалов взаимодействия вз легко получаются также и формулы для поверхностного натяжения растворов, в частности, для изотерм натяжения. Условие равновесия поверхностного слоя и объёма по компоненту i записывается как равенство полных потенциалов i , включающих идеальное слагаемое ид= идо+ RTlnC, потенциал химических взаимодействий вз и член i, выражающий действие натяжения:

вз i - взv i i = RTlnCi/Civ = 0 .

Здесь  - парциальная молярная площадь компонента в поверхностном слое; величина i= вз i -взv i выражает работу выхода компонента в поверхностный слой. Переходя от объемных концентраций к мольным долям Ni=Ci/Ci, из условия Ni=1 получаем:

(V/V)Niexp(i-i)/RT = 1 . ( 5.14)

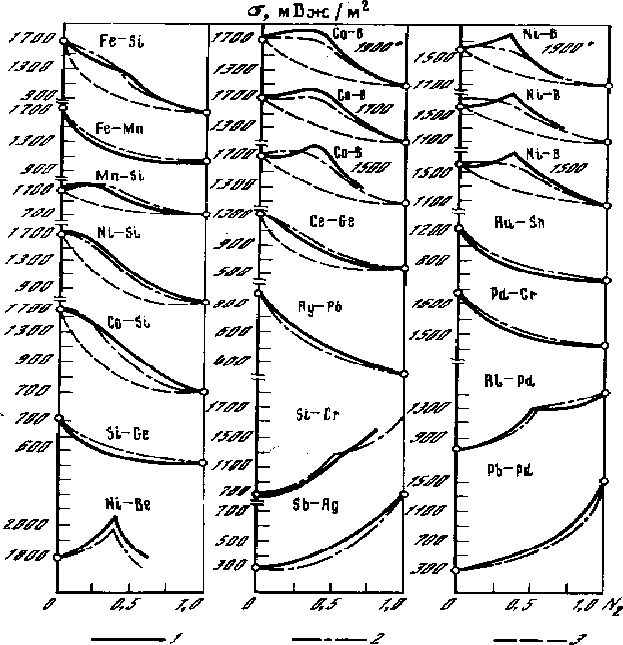
Рис. 5.6. Изотермы поверхностного натяжения бинарных систем: 1- опытные, 2- рассчитанные по уравнению (5.14), 3- идеальная изотерма Жуховицкого А. А. Уравнение (5.14) описывает изотермы с максимумом, минимумом, перегибом и др.

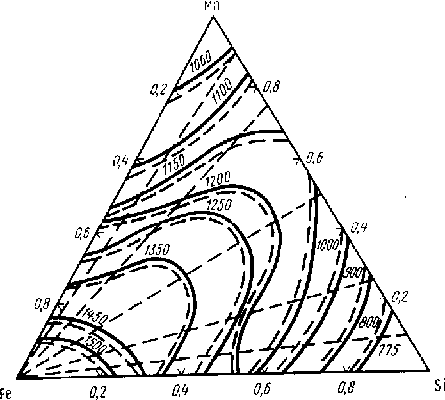
Рис.5.7 Расчётные (сплошные) и опытные (штриховые) линии равного натяжения в тройной системе Fe - Si - Mn

Это уравнение и решает поставленную задачу; оно определяет натяжение раствора  в виде неявной функции концентраций Сi и температуры Т, причем интенсивность взаимодействия компонента в растворе характеризуется концентрациями частиц в растворе и в парах; вз= RTln(Cр/Cп) и может быть рассчитан по парциальному давлению пара. Это уравнение с успехом применялось для определения абсолютных значений натяжения раствора  и поверхностной активности компонентов d/dN по давлениям паров и другим термодинамическим данным [22,179]. Однако в основном его использовали для определения вида политерм и изотерм поверхностного натяжения растворов. В этом случае натяжения чистых веществ io считаются известными, а концентрационная зависимость парциальных площадей i, натяжений i и работ i выхода в поверхностный слой определяются уравнениями:

i = ioio -iRTlni = ii ;

i = No^1/3Vж^2/3,

i - объемные коэффициенты активности. В случае идеального бинарного раствора, при близких размерах частиц (парциальных объёмах) уравнение (5.14) переходит в формулу Шишковского, которую выводят интегрированием адсорбционного уравнения Гиббса при адсорбции, определенной по формуле Ленгмюра. При неодинаковых, но не зависящих от концентрации размерах частиц из (5.14) получается формула Жуховицкого, а в случае многокомпонентной системы - современные уравнения изотерм Спроу-Праузнитца и Эрикссона (подробнее см. [179,22]).

Уравнение (5.14) позволило, по видимому, впервые, описать сложные неидеальные изотермы с точками перегиба, максимума, минимума и др. (рис. 5.6, 5.7). В связи с этим уравнение (5.14) широко применялось многими исследователями для описания сложных изотерм натяжения в различных исследовательских центрах СССР: в Свердловске, Киеве, Москве, Тбилиси и др.; примерно в 50 диссертациях оно было одним из основных или основным приемом анализа (подробнее см. фундаментальную монографию С.И. Попеля [179]) .

Интересно, что отклонения изотермы поверхностного натяжения pаствора от идеальной кривой при этом оказались связаны в основном с изменениями парциальных объёмов компонентов и, соответственно, парциальных площадей i = No1/3Vж2/3. В предшествующих работах неидеальность раствора по натяжению связывали обычно с концентрационными изменениями энергии взаимодействия; задача описания неидеальной изотермы натяжения сводилась к построению теории коэффициентов активности в поверхностном слое.

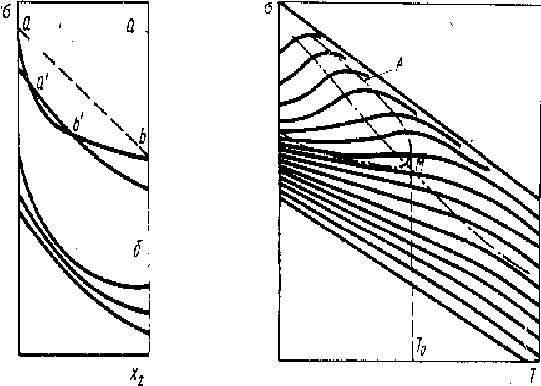
Рис. 5.8. Вид политерм поверхностного натяжения двойной системы. В области , ограниченной штриховой кривой, температурный коэффициент — положителен, а на границе наблюдается “температурная буферность” поверхностного натяжения

С помощью уравнения (5.14) был успешно описан ряд закономерностей поверхностной активности компонентов раствора. Получила описание также “температурная буферность” поверхностного натяжения. Семейство политерм поверхностного натяжения раствора имеет вид - рис. 5.8. Температурный коэффициент натяжения d/dT чистых веществ отрицателен; в растворе к нему добавляется второе, адсорбционное положительное слагаемое; при нагреве адсорбция уменьшается, что ведет к увеличению натяжения . В результате появляется область температур и концентраций, в которой второе слагаемое преобладает и температурный коэффициент d/dT раствора в целом становится положительным, (см. рис 5.8).

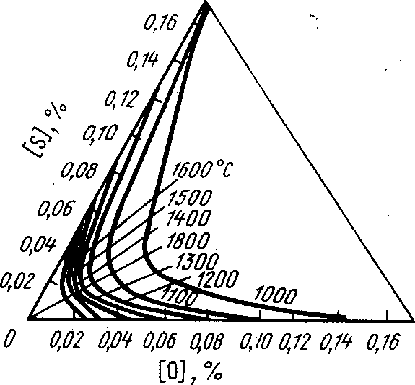
Рис. 5.9. Взаимное усиление поверхностной активности серы и кислорода в железе. При аддитивной поверхностной активности линии равного натяжения - прямые.

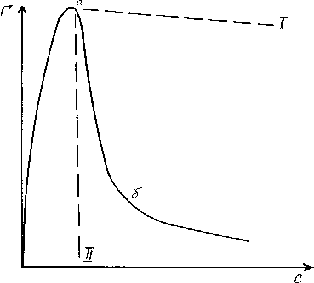
Рис.5.10. Аномальные изотермы адсорбции по Гиббсу. Участок (аб) изотермы противоречит термодинамике, так как концентрация примеси в поверхностном слое убывает при росте концентрации в объёме.