5.3.3. Энтропия взаимодействия и оценки плотности упаковки, степени квантовости

Для выяснения физического смысла энтропии взаимодействия представляет интерес уравнение S - Sид = RlnVс/V [181]. Но при обычном выводе этой формулы делаются довольно грубые допущения; свободный объём Vс и энергия Uвз считаются не зависящими от температуры, и др. [181].

Известное статистическое определение свободного объёма в ячеечной модели Vс =  exp ((Uвз - Uвз^о)/kT)dV целесообразно несколько изменить, заменяя уровень дна потенциальной ямы Uвз^о средней энергией взаимодействия Uвз^ср и записать: Vс =  exp ((Uвз - Uвзср)/kT)dV . (5.4)

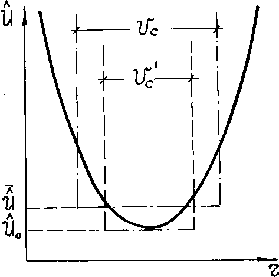
Рис.5.2. Схема статистического определения свободного объёма.

Реальная потенциальная яма заменяется термодинамически эквивалентной прямоугольной ямой с плоским дном, в пределах которой атом движется свободно. При этом реальная потенциальная яма ячейки (рис. 5.2) как бы заменяется эквивалентной ямой с плоским дном объёмом Vс таким образом, что энергия, энтропия и другие термодинамические функции системы не изменяются в результате такой замены взаимодействия (ямы).

Уравнение Fвз= kTlnQвз можно записать в следующем виде:

Fвз = Uвз + (kT*ln exp((Uвз - Uвз^cp)/kT)*d )/ . (5.5)

Здесь d= dq₁₁ dq₁₂...dq_3N -элементарный объём в координатном фазовом пространстве,  = VN - его полная величина. Так как Fвз=Uвз - TSвз, то из формулы (5.5) следует:

Sвз = k*ln /c , (5.6)

где c =  (exp(Uвз - Uвзcp)/kT)d(5.7)

Сравнивая последнюю формулу (5.7) с определением свободного объёма (5.4), замечаем, что величина с имеет смысл свободного 3N -мерного координатного фазового пространства. Здесь также можно считать, что сложная реальная 3N-мерная энергетическая поверхность Uвз= f(q₁₁,q₁₂ ...q_3N) заменяется эквивалентной совокупностью 3N-мерных ям и ложбин, в пределах которых фигуративная точка системы свободно движется по законам идеального газа, как и атом в яме с плоским дном, (см. рис. 5.2). Другие точки объёма ямы на рис. 5.2, не входящие в свободный объём, считаются не доступными для частицы; недоступными предполагаются и участки полного фазового пространства, не входящие в с.

Часто с той или иной точностью можно выделить группы из небольшого числа n координат так, что изменения энергии взаимодействия по данным координатам будут зависеть только от них, Uвз= f(q₁, q₂,...q_n). Тогда в свободном фазовом пространстве выделяется множитель, характеризующий свободный n-мерный фазовый объём cⁿ:

cn =  ... exp(Uвзⁿ - (Uвзⁿ)^cp)/kT*dⁿ

и соответствующий вклад данной группы координат в энтропию взаимодействия Sвз = klnⁿ/cⁿ. При n = 1, 2 ,3 ,6 приходим соответственно к понятиям свободной координаты qc (амплитуды колебаний ), свободной площади c, свободного объёма Vc, свободного шестимерного координатного пространства c⁶, выражающего стеснённость перегруппировок двух частиц, и т.д.. При этом

Sвз  k*ln(/с)  ...  (3R/n)*ln(ⁿ/сⁿ)  (R/2)*ln^/с^{6 }

R*ln(V/Vc)  (3R/2)*ln(c)  3R*ln(q/qc). (5.8)

Получается ряд последовательных приближений к точной формуле Sвз = kln/с. Каждое последующее приближение выражает стеснённость всё более сложных движений. В первом приближении Sвз  3Rln(q /qс) вещество как бы представляется в виде совокупности 3N независимых осцилляторов с амплитудой колебаний, равной свободной координате qс. Свободный объём даёт третье приближение, пригодное в случае ячеечной модели, когда каждая из N независимых частиц помещена в постоянную потенциальную 3-мерную яму. Влияние одних частиц на колебание других, перегруппировки атомов и другие “колллективные” эффекты не описываются в рамках модели свободного объёма; для их описания необходимы более многомерные пространства c.

Из приведенных формул виден физический смысл энтропии взаимодействия: величина Sвз выражает плотность упаковки или степень стеснённости частиц силами взаимодействия. В результате действия сил связи интервал разрешённых движений в среднем по каждой координате сокращается в q/qс раз по сравнению с идеальным газом, в котором взаимодействие отсутствует. Фигуративная точка системы движется практически лишь по свободным или разрешённым 3N-мерным энергетическим “ямам” и “ложбинам”, доля которых в полном фазовом пространстве составляет с/.

Энергия и характер взаимодействия по различным связям могут сильно различаться, поэтому весьма различна и стеснённость по разным координатам. Для системы 3N осцилляторов энтропия взаимодействия характеризует среднее значение логарифма qс/q, для приближения свободного объема - среднюю величину Vc/V и др.

Величину свободной координаты или среднюю амплитуду колебаний можно определить различными физическими методами: спектроскопически, рентгенографически, по степени размытия линий рентгенограммы и др. Результаты термодинамических расчётов qc по энтропии взаимодействия удовлетворительно согласуются с данными физических определений.

Приведём расчёт Sвз из ширины потенциальной ямы Uвз=f(r). Около “дна”, при r  rо, яму можно считать, как обычно, параболической, так что Uвз(r)-Uвзо = =Uвз*d(r - rо)2. Для потенциалов 6-12, 4-12 численный расчёт коэффициента d даёт соответственно d=0,30rо и 0,45rо; в случае более широкой ямы электростатического взаимодействия 1-12 получается d=0,7rо , в среднем 0,45rо; имеем (подробнее [7]):

Sвз = 3Rln(Uвз^о/0,3*RT)^1/2; Sвз = 1,5RlnUвз + const . (5.9)

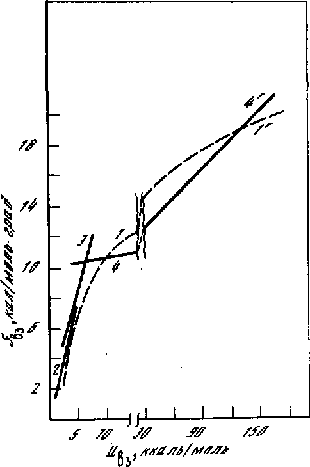
Рис. 5.3 Расчётная кривая (1,11, формула 5.9) для энтропии взаимодействия передаёт три линейные зависимости компенсационного эффекта соответственно для газов (2), жидкостей, включая растворы (3,31), и кристаллов 4 и 41 [180]

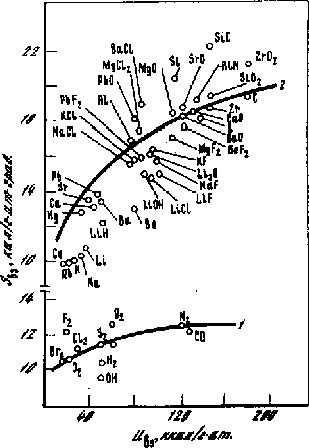
Рис. 5.4. Сопоставление расчётных кривых компенсационного эффекта для кристаллов (2) и двухатомных газовых молекул (1) с опытными данными (точки [180])

На рис. 5.3, 5.4 зависимость (5.9) сопоставлена с корреляциями Sвз - Uвз, полученными Е.С. Рудаковым [180]. Видно, что простая формула (5.9) качественно правильно передаёт зависимость энтропии взаимодействия от прочности связи Uвз в реальных газах, жидкостях, кристаллах, а также в случае внутримолекулярного взаимодействия в двухатомных газовых молекулах.

На рис. 5.5 представлен общий вид температурной зависимости свободной координаты, энтропии взаимодействия и Fвз от приведённой температуры T/= kT/h в соответствии с теорией теплоёмкости Дебая. При свободной координате qc плотность упаковки Y=Yо(1-qc/q)3, где Yo - плотность в плотнейшей упаковке, равная 0,754 для решеток ГЦК и ГПУ.

Здесь появляются две интересные характеристики вещества, рассчитываемые термодинамически: 1) Максимальное значение энтропии взаимодействия Sвзmax, (см. рис 5.5; 2)Предельное значение при T0 свободного фазового пространства или, упрощенно, свободного объема; предельное значение плотности упаковки атомов.

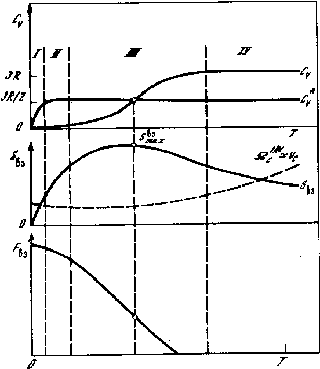
Рис. 5.5. Схема температурной зависимости свободного объёма, энтропии взаимодействия и потенциала Fвз

Через Sвз можно определить и интенсивность квантовых эффектов атомарной системы. Действительно, величина квантовых поправок к термодинамическим свойствам системы определяется величиной пространства, в котором стеснены или локализованы атомы. Квантовая неопределённость импульса p для атома, локализованного в пределах свободной координаты qc, равна, согласно соотношению неопределённостей, p= h/qc. Фермиевская энергия частиц, локализованных в пределах свободного объёма Vc: Uf = const/mVc^2/3 и т.д.

В концепции свободного объёма Vс или свободного фазового пространства с полная энтропия реальной системы равна энтропии идеального газа, помещённого в объём Vс ( или в пространство с).

Квантовые поправки Aкв к свойствам вещества равны соответствующим поправкам к свойствам идеального газа в объёме Vс:

Aкв = A - Aкл = Aкв - Aкл ,

причем величина квантового свойства Aкв здесь берется по формулам идеального газа при Vид = Vс, то есть при Sид = S. Соответствующие формулы для величины квантовых поправок к свойствам идеального газа при заданном объеме Vид= Vс можно взять, например, в [182].

Полную энтропию можно считать мерой интенсивности квантовых эффектов, “мерою квантовости” системы. Если система приближается к “чисто квантовому” состоянию, kT/h  0 при Т  0 или Vс  0, то энтропия стремится к нулю, S 0. В теории теплоёмкостей Дебая квантовый параметр h/kT и квантовые поправки также являются однозначными функциями полной энтропии, как и в приведенной концепции свободного фазового пространства или, упрощенно, свободного объёма. Так, при величине энтропии S = 0,78R квантовый параметр составляет h/kT = 4,0; теплоёмкость Cv понижена по сравнению с классическим значением Cv = 3R наполовину, Cv = 3R - 3/2R = 3/2R; квантовая поправка к энергии: Uкв -1,7RT , к энтропии; Sкв~ -7,3R , к потенциалу; Fкв= 5,6RT . Примерно этому состоянию соответствует лёд в точке плавления.

В реальных многокомпонентных веществах (и особенно в молекулярных) жёсткость связи, масса атома, частоты  и параметры h/kT по разным координатам могут сильно отличаться. Приведённое определение степени квантовости даёт в этом случае при повышенных температурах среднеарифметическое значение логарифма частоты, (ln)ср. В квантовой области закон усреднения более сложный.

Таким образом, интенсивность квантовых эффектов и величина квантовых поправок легко определяются через полную энтропию S, а параметры плотности упаковки атомов, такие как, свободный объём, свободная координата и др. - через энтропию взаимодействия Sвз. Эти способы оценок широко применялись ранее [7] и используются в следующей главе.

Зная плотность Y упаковки атомов (или c, а упрощенно-свободный объём системы), можно далее определить все кинетические коэффициенты, например, по формулам теории жестких сфер [77,78]; в итоге получается выражение кинетических свойств через энтропию взаимодействия [7]. Такие формулы удобны для оценок, так как кинетические свойства легко определяются по общедоступным термодинамическим данным; в области простой жидкости получается хорошее совпадение с экспериментом [7]. Cо вступлением в интервал затвердевания обсуждаемые формулы начинают давать более высокую подвижность частиц, чем в действительности, как и уравнения модели жестких сфер, коррелятивных функций, компьютерные эксперименты и др. Подвижность частиц в вязкой жидкости или в твердых телах ограничивается не плотностью упаковки частиц, но качественно иными эффектами, стабилизирующими структуру.