4.1.6. Устойчивость соединений. Выделение химического и структурного слагаемых в энергии взаимодействия

Мерою устойчивости механической системы ( в простейшем случае - частицы в потенциальной яме) является, как известно, величина d²U/dX² (кривизна потенциальной ямы); аналогично можно определить и устойчивость структуры твердого тела, молекулы или кристалла, причём часто наиболее интересны минимальные значения d²U/dX², характеризующие лёгкие перегруппировки - минимальные частоты min, или мягкие моды.

Мерою устойчивости структуры к изменениям концентрации N также можно считать величину второй производной d²U/dN², точнее - d² F/dN²;  F - изменение потенциала F при образовании раствора. Если кривизна d²F/dN² всюду положительна, то растворимость неограниченная. Если на политерме F - N имеется участок отрицательных значений второй производной, то около его появляется область нерастворимости (расслоения), см. рис. 4.3. Чем больше кривизна d²F/dN² или чем выше устойчивость, тем меньше растворимость (см. рис. 4.3).

Наиболее устойчивые соединения обычно имеют минимальные области нестехиометричности (растворимости). Если растворимость компонента В в растворителе А равна N, то для процесса растворения В в А можно записать: U  F^o  RTlnN. Это уравнение позволяет оценить энергию взаимодействия компонента В, растворённого в А, на границе растворимости (в насыщенном растворе). На рис. 4.4. представлена характерная кривая зависимости энергии взаимодействия от состава, полученная с помощью таких оценок. Кривая относится к системе с четырьмя соединениями. Видно, что энергия взаимодействия Uвз естественно распадается на два слагаемых, качественно различных:

1. Энергия обычных взаимодействий, плавно зависящая от состава по кривой с максимумом примерно посередине диаграммы; эта изотерма подобна характерным изотермам квазихимических растворов и опытным изотермам в области простой жидкости ( сплошная кривая).

2. Энергия Uст стабилизирующих структуру эффектов, которая изменяется по сложной кривой с острыми максимумами; каждый максимум соответствует соединению (верхняя кривая).

Кривизна d²U/dN² по второму слагаемому (по стабилизирующим эффектам) многократно превосходит соответствующую величину по обычным химическим связям. Устойчивость соединений d²U/dN² и растворимость определяются практически одними лишь стабилизирующими структуру эффектами. Если бы не было второго (стабилизирующего) слагаемого , то политермы Uвз - N были бы плавными и получилась бы неограниченная растворимость.

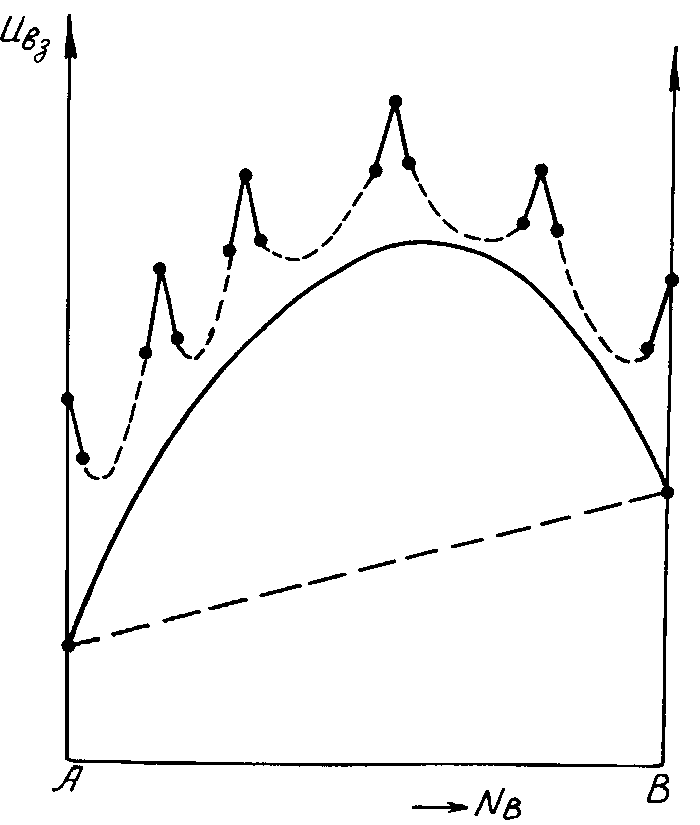
Рис. 4.4. Политерма энергии Uвз двойной системы. Энергия распадается на обычное медленно изменяющееся квазихимическое слагаемое Uх и структурное Uст с резкими максимумами

Этот случай и реализуется при переходе к состоянию простой жидкости, в которой второе слагаемое исчезает, Uст = 0. Первое слагаемое обычных связей мало изменяется при переходе от твердого тела к простой жидкости.

Следует отметить, что реальная политерма Uвз- N ещё намного сложнее, чем на рис. 4.4, и, соответственно, ещё дальше от простой плавной политермы типа квазихимической, которая получается в традиционной модели. Действительно, новые методы эксперимента убеждают, что мы знаем далеко не все соединения. В последнее время число известных соединений и структур быстро возрастает, в частности, в связи с применением новых методов быстрого переохлаждения и стеклования расплавов, получения аморфных металлов. Так получены качественно новые структуры - квазикристаллы, имеющие дальний порядок без периодической структуры [142]. Выявляется много новых стабильных и метастабильных соединений. Это означает, что на политермах (см. рис. 4.4) стабильных соединений и соответствующих максимумов Uвз, по-видимому, значительно больше, чем мы знаем в настоящее время. Далее, между высокими максимумами стабильных соединений имеется ещё много более низких максимумов, соответствующих метастабильным соединениям. Кроме того, изотермы энергии, вязкости, прочности и других свойств и в области растворов не сводятся к монотонным кривым; они содержат много особенностей, в частности, осцилляций. При этом прослеживается подобие таких особенностей у кристалла и у жидкости [143]. Нет надежды получить что-либо подобное этой сложной реальной картине в рамках традиционной модели, которая даёт лишь плавные изотермы (см. рис. 4.3).

Таким образом, вид изотерм энергии в бинарных системах и их изменение с температурой также свидетельствует о наличии качественно иного эффекта по сравнению с тем, что дает традиционная модель; видимо, это структурные стабилизирующие взаимодействия Uст.

4.1.7. "ОДНОНАПРАВЛЕННЫЕ" ВЛИЯНИЯ ПРИМЕСЕЙ

Как известно, в квантовой области результат взаимодействия двух частиц зависит от того, можно ли их считать идентичными, или же их следует рассматривать как различные. Если стабилизирующие структуру силы Fст обусловлены квантовыми эффектами в атомарной системе, то влияние добавки на структурно-чувствительные свойства также должно зависеть не только от ее химических характеристик, но и от того, можно ли считать атомы добавки практически идентичными атомам матрицы, или же принципиально отличными от них. В этом случае все инородные добавки, независимо от их химических свойств, могут давать изменения свойств одного знака. Действительно, в твердом состоянии наблюдаются подобные "однонаправленные" влияния.

Хорошо известно, что добавление к чистому кристаллическому веществу примеси любого другого инородного вещества приводит к повышению прочности и хрупкости; неизвестны факты обратного влияния, то есть понижения хрупкости при любых химических свойствах добавки. У металлов, кроме того, инородные добавки, видимо, всегда повышают электросопротивление. Инородная добавка почти всегда понижает также температуру плавления исходного чистого вещества; двухкомпонентные системы более легкоплавки по сравнению с чистыми веществами, состоящими из идентичных атомов. Имеются также системы, в которых перечисленные эффекты малозаметны, а атомы добавки "ведут себя" практически как атомы матрицы. Такие системы имеют"сигарообразные" диараммы плавкости и неограниченную растворимость в твердом состоянии. Очевидно, такие влияния связаны со стабильностью структуры, это "Fст- эффекты". В системах с нулевой жесткостью структуры (Е= 0), то есть у простых жидкостей и плотных газов, насколько нам известно, не встречаются такие "однонаправленные" влияния любых инородных примесей. Tемпературы кипения и критической точки, вязкость бинарной системы и др. обычно повышаются примесями, если их молекулы (атомы) вносят в систему более прочные взаимодействия, и понижаются при внесении более слабых связей. Легкоплавкость бинарных систем по сравнению с чистыми веществами связана с тем фактом, что твердые растворы относительно менее выгодны энергетически; растворимость в твердом состоянии обычно ниже, чем в жидком. Малая растворимость означает, что бинарная система в твердом состоянии имеет повышенный термодинамический потенциал F. Если растворимость двух компонентов незначительна, то моль их примерно эквиатомной эвтектической смеси имеет потенциал F, повышенный на F RTln2 по сравнению со случаем образования их идеального раствора. Такое повышение F твердого состояния приведет к понижению температуры плавления на

Тпл  F/Sпл  RTплln2/Sпл  Tплln2  0,69Тпл ,

если Sпл  R в соответствии с правилом Гильдебранда. Температура плавления такой эвтектики будет понижена на Tпл  0,69Тпл, то есть более чем наполовину. Если предположить обратный случай, когда в твёрдом состоянии растворимость неограниченная, а в жидком - небольшая, то обычный термодинамический анализ такой гипотетической системы привёл бы к "перевёрнутой" эвтектической диаграмме, в которой эвтектика была бы самым тугоплавким составом, (рис.4.5). Легкоплавкость реальных двухкомпонентных систем, в частности, эвтектик, отражает понижение стабильности твердого вещества при добавлении почти любых инородных атомов. В кристаллическом состоянии более стабильны решётки из одинаковых атомов - чистые вещества. Приведенные температуры плавления (Tпл/Uвз) у них максимальны.

Обсуждаемый эффект незначителен у систем с сигарообразной диаграммой плавления. Характерно, что такие двойные системы с неограниченной растворимостью в твердом состоянии, на которых малозаметно обсуждаемое влияние идентичности атомов, не встречаются у легких элементов, то есть у атомов с наибольшей величиной квантовых эффектов. Нам не удалось найти непереходный элемент легче германия (атомный вес - 72,6), который давал бы неограниченную растворимость в твердом состоянии с каким-то более легким компонентом. Германий дает такую диаграмму с кремнием.

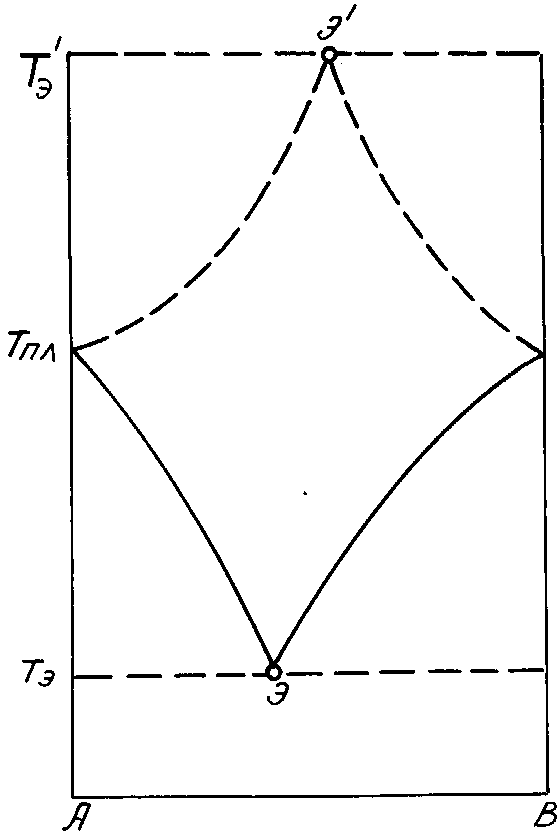
Рис. 4.5. Перевернутая эвтектическая диаграмма

При традиционном анализе удивительные "однонаправленные" влияния примесей часто остаются незамеченными, а закономерности растворимости связывают, естественно, с химическими свойствами - с энергией взаимодействия, характером связи, размером внедряемых атомов и др. [144]. Тем более показателен тот факт, что установлены эмпирические правила, связывающие растворимость с соотношением атомных весов компонентов [144], хотя атомный вес, по традиционным представлениям, не должен влиять на растворимость.

Так как растворы обычно менее склонны к затвердеванию по сравнению с чистыми жидкостями, то на их основе легче, очевидно, получить и незамерзающие квантовые жидкости. В многокомпонентной системе легких элементов H - H₂ - D - D₂- ³He - ⁴He - Li ... имеется, вероятно, широкая область незамерзающих растворов (стабильных и нестабильных), в том числе и без участия или почти без участия изотопов гелия.

Отметим,что обычно не только твёрдые растворы и смеси, но и твёрдые соединения относительно менее стабильны и более легкоплавки по сравнению с чистыми веществами. Так, оксид алюминия плавится при 2050 ^oС, оксид кальция - при 2570 ^oС, а их соединение Ca₂₄Al₁₄O₄₅ при 1455 ^oС, хотя прочность связи в нём больше; оно образуется с тепловым эффектом около 200 кДж/моль [30]. Приведённая температура плавления соединения Tпл/Uвз в данном случае примерно вдвое ниже, чем у образующих его чистых окислов. Если в этой системе CaO - Al₂O₃ соединить кривой точки плавления соединений, то получатся линии, подобные линиям ликвидуса в простой эвтектической диаграмме, (см. рис 4.5). Образование соединений здесь дает лишь малые поправки к общему виду диаграммы.

Отметим также, что при традиционном подходе трудно дать ясное определение широко применяемому термину "структурно-чувствительные свойства".

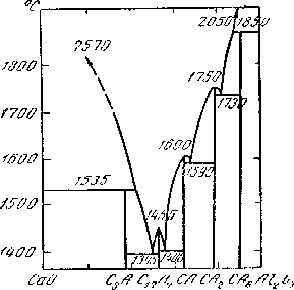
Рис. 4.6. Диаграмма плавкости системы CaO-Al2O3

С точки зрения предлагаемой модели структурно-чувствительными являются свойства, обусловленные стабилизирующими структуру эффектами, энергией Uст, и связанные с жесткостью структуры; это "Fст- свойства". Таковы энергии активации Е, повышенная вязкость или прочность, зависящая от характера зернистой структуры поликристалла, то есть от "надмолекулярной структуры", от Fст-структуры. Часто малочувствительны к структуре, например, объём или энергия взаимодействия жидкости, которая даже в твёрдом состоянии часто на 95% и более определяется обычными взаимодействиями (Uст  Hпл< 0.05Uвз).

В материаловедении структурно-чувствительными называют свойства, которые определяются дефектностью кристалла - концентрацией дислокаций, вакансий, дислоцированных атомов, межблоковых и межзеренных границ и др. С позиций предлагаемой модели это также "Fст - свойства".

4.1.8. ИСТОРИЯ ВОПРОСА О РАЗМЫТОСТИ ПЕРЕХОДОВ. СОПОСТАВЛЕНИЕ С ТРАДИЦИОННЫМ ПОДХОДОМ

Изучение структурных фазовых переходов началось сравнительно поздно, практически лишь после появления лабораторных электропечей и термопар в конце прошлого века [28]. До этого высокие температуры определяли лишь на глаз, по цветам каления. В начале века, после работ Ван-дер-Ваальса, Кюри-Вейсса, классификации Эренфеста ситуация представлялась достаточно ясной [1,18]. Как и в других вопросах, исходным было априорное убеждение, что основные явления объясняются или объяснятся и будут описаны на основе традиционной молекулярной модели, на основе представления об упругих притягивающихся и отталкивающихся классических атомах. Эксперимент показал, что плавление и полиморфные превращения являются точечными; поэтому было принято, что в традиционной модели такие превращения также являются точечными.

Встречается мнение, что точечный характер плавления в модели доказан; иногда считают, что этого требует уже правило фаз. Известен также следующий аргумент: переходы должны идти скачком, так как симметрия может появиться или измениться лишь скачкообразно [28].

Однако со временем нарастали трудности теории [28]. Более тщательные измерения выявляли размытость все новых превращений, считавшихся ранее точечными. Сначала такую размытость объясняли "случайными" причинами, например, влиянием примесей, дефектностью решетки, гетерогенными флюктуациями и др. Но в настоящее время под давлением опытных данных распространяется убеждение, что чисто точечных переходов вообще нет в природе, есть лишь переходы, интервал T размытия которых мал (например, меньше 0,1 К) и неудобен или пока недоступен для измерения. "Почти общепризнано, что проблема фазовых переходов относится к числу сложнейших, далеких от разрешения проблем физики" [28] и др.

Теперь становится ясно, что традиционная модель недостаточна в этих вопросах; при обычных взаимодействиях атомов и классическом движении "кристаллические" свойства, отличающие кристалл от жидкости, включая точечные фазовые переходы, не появляются в этой модели и в области твердого состояния. Плавление и другие переходы в традиционной модели отнюдь не точечные, но очень размытые (Тпл  Tпл  (100-1000) К. Задача теории, следовательно, скорее обратная: требуется объяснить не тот факт, что небольшое размытие существует, Тпл  0,1 К вместо Тпл = 0; в действительности требуется объяснить, почему реальное размытие столь мало, 0.1 К, вместо величины (100-1000) К, которую мы получили бы при последовательном анализе традиционной модели.

Простейший, казалось бы, исходный вопрос: почему реакции размыты, а плавление точечное ? - не мог быть решён и, cоответственно, не ставился при традиционном подходе. Следует признать, что решетки и сетки реальных твердых тел скреплены качественно иными эффектами, весьма дальнодействующими, способными сцепить атомы в блоки, например, по 10⁵ частиц и обеспечить их переход блоками, что приводит к реальному интервалу размытия, в 10⁵ раз меньшему по сравнению с химической реакцией. Простейший, казалось бы, исходный вопрос: почему реакции размыты, а плавление точечное ? - не мог быть решён и, соответственно, не ставился при традиционном подходе. Следует признать, что решетки и сетки реальных твердых тел скреплены качественно иными эффектами, весьма дальнодействующими, способными сцепить атомы в блоки, например, по 10⁵ частиц и обеспечить их переход блоками, что приводит к реальному интервалу размытия, в 10⁵ раз меньшему по сравнению с химической реакцией. Простейший, казалось бы, исходный вопрос: почему реакции размыты, а плавление точечное ? - не мог быть решён и, соответственно, не ставился при традиционном подходе. Следует признать, что решетки и сетки реальных твердых тел скреплены качественно иными эффектами, весьма дальнодействующими, способными сцепить атомы в блоки, например, по 10⁵ частиц и обеспечить их переход блоками, что приводит к реальному интервалу размытия, в 10⁵ раз меньшему по сравнению с химической реакцией.

Независимо, но подобным же образом развивались и представления о молекулярном механизме "размытости концентрационных фазовых переходов". Считалось, что из традиционной модели можно получить наблюдаемые соединения постоянного состава в твердом теле; выявленные позднее области нестехиометричности объясняли дефектностью структуры.

Особенности соединений в твёрдом состоянии, их непохожесть на молекулярные соединения в газах и жидкостях неоднократно вызывали дискуссии крупнейших физикохимиков в прошлом [138,18]. В ХV111 и Х1Х веках преобладало мнение, что твёрдые соединения являются химическими индивидами, и для них справедливо положение Дальтона о постоянстве химического состава. Следовательно, "концентрационные фазовые переходы", как и температурные, считались точечными, а их интервал размытия, или область нестехиометричности N - нулевой. Понятие "раствор" долго относили лишь к жидкостям; понятие "твёрдый раствор" ввёл Вант-Гофф лишь в 1890 г. Правда, Бертолле развивал представление о соединениях переменного состава, однако считалось, что Пруст опроверг эти представления в известной дискуссии прямыми данными химического анализа, в частности, для карбоната меди. Менделеев считал соединения переменного состава настоящими соединениями, но частично диссоциированными. Курнаков Н.С., исследуя зависимость твёрдости, электропроводности, температуры плавления от состава, постулировал существование соединений как постоянного, так и переменного состава, как "дальтонидов", так и "бертоллидов".

С накоплением опытных данных об областях нестехиометричности главной задачей стало объяснение таких небольших интервалов размытости этих переходов. "Лишние" или недостающие атомы по отношению к стехиометрическому составу обычно рассматривали как дефекты структуры, как атомы, дислоцированные в междоузлия, или вакансии.

Но в действительности последовательный анализ в рамках традиционного подхода даёт лишь то, что наблюдается в состоянии простой жидкости, то есть лишь растворы, но не соединения. Удивительны и подлежат объяснению не отклонения от постоянного состава соединений, а само существование соединений, невозможных в традиционной модели. Предположение о том, что реакция образования соединений идет блоками, например, по 105 частиц, позволяет объяснить - почему размытость перехода или ширина области нестехиометричности в действительности в 10⁵ раз меньше, чем в модели.