3.6.8. Резюме к параграфу 3.6

Резюмируя содержание данного параграфа, можем заключить, что и здесь, в теории турбулизации, окажется, очевидно, плодотворным и результативным анализ с позиций предлагаемой молекулярной модели по принятой в этой книге схеме или "алгоритму". Как и в других вопросах, выявляются те искажения и деформации представлений, к которым при-водит наша чрезмерная вера в традиционную теорию, в данном случае - в

представление о простой ньютоновской жидкости.

Выявляется разрыв, а практически противоречие между теорией и экспериментом, которое здесь не доходит, как в предыдущих разделах, до столкновений экспериментаторов с теоретиками. Основной опытный факт - турбулентность больших потоков - здесь слишком очевиден, чтобы можно было "не признать" его с позиций теории; поэтому противоречие теории и опыта обычно сглаживается теми или иными объяснениями. Как и выше, противоречие объясняется несовершенством математического аппарата. Выявляется математизация теории, вера в то, что более совершенная математика даст описание реальной турбулизации, и что не потребуется изменять физические основы теории, учитывать неньютоновские квазикристаллические сопротивление течению, что "у нас нет причин думать, что в этом уравнении мы потеряли какие-то слагаемые".

Между тем учет этих "потерянных" твердоподобных слагаемых в сопротивлении течению позволяет сразу же получить искомое усиление случайных возмущений, то есть генерацию турбулентных пульсаций в виде простейшего уравнения для затухающих и растущих колебаний. Механизм

генерации пульсаций при этом оказывается таким же, как в известных случаях биений при сухом трении и в возбуждении автоколебаний потоков.

Существование "застудневших" участков, перемещающихся и вращающихся как целое, дает естественное объяснение вихреобразования, которое не описывается традиционной теорией. Объясняется и ряд других особенностей, включая общеизвестные "популярные" примеры. Очевидно, анализ богатого экспериментального материала по турбулентным потокам с этих позиций может быть успешным и плодотворным.

Глава 4. Зернистая, или блоковая, структура реальной жидкости

4.1. Блоки и размытость фазовых переходов

4.1.1. Температурный интервал размытия т переходов

Одно из главных отличий предлагаемой модели от традиционной состоит в том, что в предлагаемой модели эффекты, стабилизирующие структуру, считаются дально-действующими (R  1мкм), а в традиционной модели - короткодействующими (R  1нм).

Если в традиционной модели возможны лишь наноструктуры, то в предлагаемой - примерно в 1000 раз более крупные микроструктуры, блоки, зерна жидкости и др. Существование зерен с дальним порядком доказывается уже тем, что узкий луч электронного микроскопа диаметром менее микрона дает дифракционную картину рассеяния как от одного зерна поликристалла или как от правильного микрокристаллика с дальним порядком. Далее, зерна удается непосредственно наблюдать, в частности, на растровой фотографии свежеобразованной поверхности жидкого галлия [29]. Зернистая "поликристаллическая" структура жидкости приводит к ряду важных следствий, которые и рассматриваются в данной главе.

Обсудим простейший, казалось бы, вопрос: почему плавление точечное, тогда как химические реакции "размыты"? Другими словами: почему переход от кристалла к жидкости происходит при фиксированной температуре, тогда как смещение равновесия

химической реакции от преобладания исходных веществ до преобладания продуктов занимает широкий интервал температур ? Так, для реакции C+CO₂ = 2CO 1 % продуктов в газе (СО) появляется при 780 К, 50% - около 1000 К, и 99% продуктов (СО) при 1240 К. Можно считать, что "интервал размытия" реакции по температуре составляет Т=1240 - 780 = 460 К (от 1% продуктов до 99%). Отметим, что упомянутую реакцию C+СO₂= 2CO можно провести и как точечный процесс, если перейти к условиям постоянного давления. Испарение жидкости также может идти как размытый переход в закрытом сосуде ( при V=const), но может протекать как точечный переход при постоянном давлении.Чтобы не рассматривать подобные усложнения, можно ограничиться анализом перестроек структуры лишь в конденсированной фазе при незначительном влиянии внешних полей и давления. Имеется достаточно много опытных данных как о величине интервала размытия плавления Тпл , так и о скорости нарастания концентрации Сж "жидкостных" частиц (или ячеек структуры) с приближением к точке плавления (рис. 4.1, 4.2)( Конечно, здесь рассматривается не кинетическая, а термодинамическая, равновесная размытость перехода, когда к каждой точке кривой Сж-Т можно подойти с двух сторон при достаточном времени выдержки.).

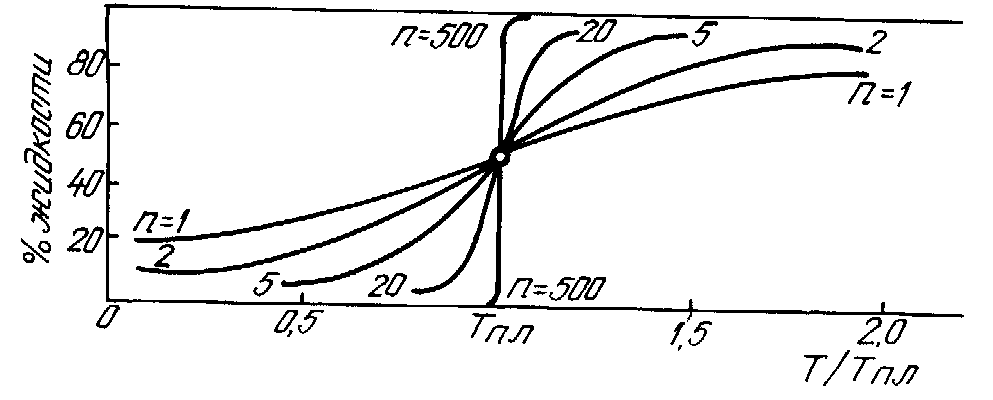
Рис. 4.1. Схема к определению размытости плавления по температуре. Показаны политермы доли "жидкостных" ячеек (частиц), полученные в предположении, что атомы переходят с "кристаллических" позиций на "жидкостные" группами по 1, 2, 5, 20 и 500 частиц. Реальный интервал размытия плавления ΔТпл соответствует переходу группами по 105 атомов

Интервал Т обычно имеет величину порядка 10^-1-10¹ К [38]. Обычно считается, что обсуждаемая размытость перехода обусловлена либо влиянием примесей, либо каких-то дефектов решетки; предполагается, что чистое кристаллическое вещество с бездефектной решеткой дало бы "абсолютно точечный" переход с нулевым интервалом размытия, Т= 0. Если у реакции есть неизвестный стехиометрический коэффициент n (например, nC+nCO₂= 2nCO) , то его можно определить (и действительно определяют) по температурной зависимости концентраций или по величине интервала Т; с увеличением коэффициента n интервал размытия Т становится более узким (см. рис.4.1):

n = RT²*[ dln(C_2co/C_co2)/dT]/H (4.1)

Аналогично можно определить и "стехиометрический коэффициент" плавления, то есть число атомов, участвующих в элементарном акте, по величине Т или по кривой Сж- Т. Получается n = (10⁴ - 10⁵). Отметим, что это термодинамическое определение n, не связанное с какими-либо модельными представлениями. Мы получили интересный результат: плавление в 10⁵ раз менее размыто по температуре, чем эквивалентная химическая реакция. Интервал размытия плавления часто примерно такой же, как у реакции со стехио-метрическая же, как и у химической реакции. Если же переход идёт большими группами, например, по 10⁵ частиц, то энергия флюктуаций kT мала по сравнению с энергией U превращения группы (U  10⁵kT), и разброс температур перехода отдельных групп мал ( 10^-1 К). Строго точечный переход (Т = 0) получится лишь в том случае, если все атомы совершают переход одним элементарным актом.

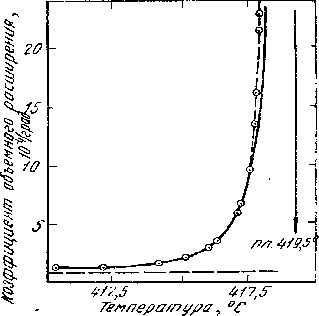
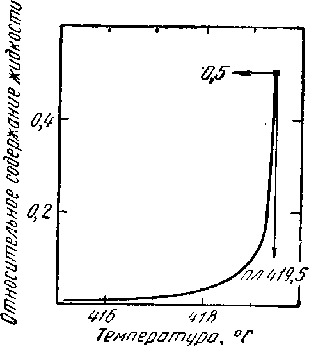
Рис. 4.2. Нарастание доли жидкости (а) и коэффициента объёмного расширения цинка (б) с приближением к температуре плавления Тпл= 419,5 oС [30]

ческими коэффициентами порядка 105, в элементарном акте которой участвуют 10⁵ частиц. "Квант плавления" составляет, видимо, в данном случае 10⁵ атомов. Для того, чтобы в молекулярной модели атомы переходили из одной структуры в другую группами по 10⁵ частиц и более, нужно, во-первых, ввести в модель достаточно дальнодействующие эффекты, сцепляющие такие группы с линейным размером (10^-6 - 10^-4) см; для этого подходит потенциал (2.1) при радиусе дальнодействия R  L  1 мкм. Во-вторых, нужно, чтобы "кванты" по 10⁵ частиц как-то отделялись друг от друга; однако в реальных кристаллах, даже в наиболее совершенных монокристаллах, имеются готовые блоки [28], обычно с небольшой разориентацией решёток порядка 1⁰, разделённые цепочками краевых дислокаций.

Полученные значения интервалов размытия можно пояснить следующим образом. Если атомы переходят из "кристаллических" позиций на "жидкостные" индивидуально, поодиночке, то энергия флюктуаций kT значительна по сравнению с энергией перехода, U  kT, и получится большой флюктуационный разброс температур переходов отдельных атомов около среднего значения Тпл.

Интервал размытия Т будет по порядку величины таким же, как и сама температура плавления, Т  Тпл (см. рис.4.1, кривая 1). Размытость плавления будет такая же, как у химической реакции. Если же переход идёт большими группами, например, по 10⁵ частиц, то энергия флюктуаций kT мала по сравнению с энергией  U превращения группы (U  10⁵ kT), и разброс температур перехода отдельных групп мал (10^-1K). Строго точечный переход (T = 0) получится лишь в том случае, если все атомы совершают переход одним элементарным актом.