3.6.5. Концентрация течения в отдельных плоскостях

Выше рассмотрена генерация или усиление колебаний скорости течения в данной плоскости; рассматривается неравномерность течения по времени. Однако при твёрдоподобном сопротивлении будет возбуждаться и неравномерность в распределении течения по параллельным плоскостям, в которых оно развивается (то есть по плоскостям, параллельным вектору скорости сдвига). При твёрдоподобном сопротивлении, когда f = kV + c, k < 0 , течение будет концентрироваться в некоторых плоскостях. Если даже исходное распределение течения по плоскостям близко к равномерному, в той плоскости, где оно оказалось несколько быстрее, сопротивление f будет меньше, что даст ускорение течения и дальнейшее уменьшение сопротивления, дальнейший рост V и уменьшение f и т. д. При линейной зависимости f от v получится экспоненциальное ускорение течения в этой плоскости, то есть самоускоряющееся нарастание неравномерности течения.

Подобные процессы действительно наблюдаются в твёрдых телах, особенно при деформации монокристаллов, когда им не мешают межзёреные границы. Так, при медленном растяжении монокристалла цинка всё течение сосредоточивается в одной или нескольких плоскостях скольжения; вся деформация идёт через "соскальзывания" и "защёлкивания" скольжения в какой-то плоскости, часто с характерным звуком, с потрескиванием [12]. Отметим, что физической причиной уменьшения сопротивления f с ускорением течения, с ростом V, является ослабление в результате течения тех структур, которые поддерживают жесткость сетки или решетки, прочность и вязкость. Неограниченное развитие такого процеса привело бы к разрушению образца ( кристалла или жидкости ) по рассматриваемому сечению. Однако обычно в кристалле разупрочнение деформацией сменяется упрочнением, "наклёпом" и течение в плоскости " защёлкивается". В жидкости прекращение быстрого течения, сконцентрированного в определённой плоскости или на "поверхности тангенциального разрыва", может идти по механизму " разбалтывания" этой плоскости, самопроизвольного роста возмущения или "ряби" на такой плоскости [134].

В монокристаллах плоскости скольжения, в которых сосредоточена почти вся деформация, выявляются металлографически или видны визуально. У вязких жидкостей также видны после перемешивания подобные полосы скольжения. Так, в охлаждённом глицерине (например, при температуре t = -20 ^oC, ~10 Па*с) после перемешивания в течение нескольких минут видны подобные более светлые полосы, по которым прошла наибольшая деформация сдвига.

3.6.6. Образование вихрей

Для идеальной жидкости справедлива теорема о сохранении ротора; вихри в ней не образуются. Они не образуются, согласно имеющимся аналитическим решениям, и в реальной жидкости (с ненулевой вязкостью) при обтекании шара, цилиндра, при плоскопараллельном течении и в других случаях при определенных условиях симметрии. Эксперимент подтверждает, что вихри не образуются и в соответствующих реальных потоках при малых Re, однако они появляются при увеличении Re, например, уже при Re = 30 в случае обтекания цилиндра, задолго до турбулизации потока. Появление вихрей часто является первым признаком несоответствия реального течения теоретическим решениям. Представление о неоднородности течения в реальной жидкости позволяет устранить и это противоречие теории и эксперимента.

Действительно, если в жидкости имеется градиент горизонтальной скорости V по высоте h, то взвешенный в ней твёрдый шарик будет поворачиваться со скоростью dV/2dh из-за разности скоростей V = 2R*dV/dh на уровне верхнего ("h" велико) и нижнего полюсов шарика (рис. 3.28).

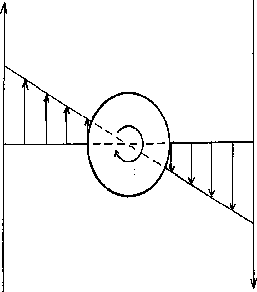
Рис. 3.28 Схема генерации вихря при существовании застудневших участков жидкости, перемещающихся и вращающихся как целое

Если в жидкости имеется взвесь таких шариков радиусом R или "застудневших" недеформируемых участков самой жидкости, и на них приходится доля 1 -  массы, то в результате течения появляется момент вращения M, равный примерно:

M = 1/6(1-)R*dV/dh

на единицу массы жидкости. По интенсивности вихреобразования можно оценить размер R " застудневших " участков. Например, в опытах по обтеканию цилиндра в периодическом режиме за каждый период T, равный примерно 2R/V, от цилиндра отслаивается вихрь с моментом M порядка M ~10^-2mVR, где m- масса жидкости в объёме цилиндра, V- скорость потока, R- радиус цилиндра, составляющий во многих экспериментах несколько сантиметров.Оценка даёт для размера R недеформируемых участков жидкости значение порядка 100 мкм. При медленном течении ( Re < 20 ) величины M и R незначительны. Рост вихрей, как и рост турбулентности с увеличением скорости V, соответствует увеличению масштаба неоднородности течения.

Вполне естественно, что гораздо большие, чем у воды, моменты сил M возникают при течении студней или растворов студнеобразующих полимеров, в которых застудневание и твёрдоподобные эффекты более явно выражены; в этих системах недеформируемые области велики и более устойчивы. Для таких жидкостей разработаны специальные методики измерения моментов M вращения сил, возникающих при сдвиге; вискозиметрия заменяется реометрией [32].

Таким образом, традиционные решения не отражают вихреобразования, как и генерацию пульсаций. Вихреобразование или появление моментов вращения M также объясняется при учёте неоднородности течения, при учете существования застудневших участков жидкости, которые перемещаются и поворачиваются при течении как целое.