3.6.3. Механизм генерации пульсаций в потоке при твердоподобном сопротивлении течению

Из приведенного обзора видно, что задачу о генерации пульсаций или о самопроизвольном нарастании возмущений практически не удается решить при традиционном подходе. Между тем эта задача решается легко, в рамках простейших уравнений для колебаний, если учесть твердоподобные свойства жидкости, в частности, выявленные в параграфе 3.2. Генерацию колебаний при этом можно проследить даже на простейших примерах течения и на общеизвесных "популярных" аналогиях.

Как отмечено в параграфе 2, твердоподобное сопротивление застудневшей жидкости f, в отличие от обычного вязкого, убывает, но не возрастает с ростом скорости сдвига v: f = kv + c , причём в случае вязкого сопротивления c = 0 , а коэффициент k пропорционален или равен вязкости. Равенство k =  выполняется, в частности, если угловая скорость течения V=d/dt численно равна линейной скорости течения, а площадь равна единице. Будем далее предполагать этот случай, k = . В "твёрдоподобном" случае k < 0, "c" велико. Для малых колебаний, развивающихся в узком интервале скорости V, коэффициент k можно заменить производной df/dV.

Для простоты рассмотрим примеры течения, соответствующие одномерной динамике материальной точки, а не трёхмерной динамике сплошной среды. Пусть опорные плоскости C, C1 с трубкой C2 (рис. 3.26) равномерно движутся влево со скоростью Vo . Идёт течение, так как рассматриваемый объём жидкости удерживается упругим элементом - пружинкой с закреплённым концом А или объёмом газа под закреплённым поршнем А1 (Рассматриваемые объёмы жидкости (см. рис. 3.26) можно считать микрообъёмами в потоке; внутри самих микрообъёмов течение считается ламинарным. ). Как всегда, имеется стационарное решение, в данном случае очевидное: течение идёт со скоростью Vo ; точки Б, Б1 , Б2 неподвижны; силы инерции fи = m*d²x/dt² равны нулю; пружинки (или газ в случае "б") растянуты до такой длинны l_o, что сила упругости fу = K₂*l компенсирует силу вязкости f = V.

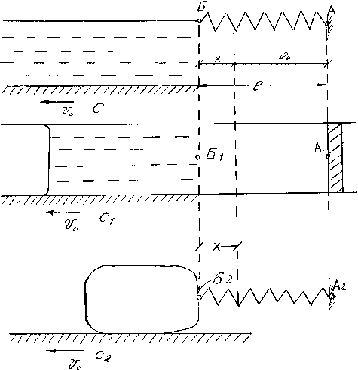
Рис. 3. 26. Схема к выводу уравнений усиления колебаний скорости течения при твёрдоподобном сопротивлении. Концы пружинок А, А1 и поршень А2 неподвижны, опоры С, С1 и трубка С2 равномерно движутся влево. 2-стационарное растяжение пружинок и газа, Х- добавочное колеблющиеся удлинение

Добавим к стационарному течению Vo малое возмущение; для этого дополнительно растянем пружинку на х ( l = l_o + х ) и придадим течению (смещению х точек Б, Б1, Б2 ) дополнительную скорость V1=dx/dt. Сила упругости возрастает на fу = K₂x, вязкое сопротивление на f = kV1. Получится обычное [135] уравнение колебательного движения:

fи + f + fу = 0 или m*d²x/dt² + k*dx/dt + k2x = 0 с решением [135]:

x = A*exp(-k/2m)*sin(t + ) (2.2)

Частота колебаний  равна  = (k₂/m)^1/2.

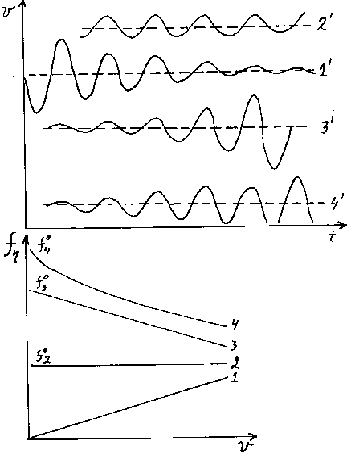
Рис. 3.27. Усиление колебаний скорости течения. При вязком сопротивлении(1) колебания затухают; при постоянном сопротивлении (коэффициенте трения) (2) колебания неизменны (2); при "твёрдоподобном" сопротивлении (3,4) колебания усиливаются и переходят в движение скачками (3I,4I)

Интересно следующее: в показателе экспоненты в (2.2) стоит угловой коэффициент "k" зависимости f = kV + c или производная df/dv. При вязком сопротивлении f = kV, k =  > 0 и , естественно, колебания затухают, причем скорость затухания пропорциональна вязкости. Но в "твёрдопо- добном" случае k < 0 и получается не затухание, но экспоненциальное усиление колебаний. При этом по абсолютной величине k обычно много больше , abs(k) >> , поэтому колебания усиливаются быстрее, чем затухают.

Это соответствует следующему реальному случаю: поток может быстро турбулизоваться при прохождении какого-либо сопротивления, затем медленно успокаиваться. Турбулентный "след" после прохождения корабля может быть заметен, например, в течение часа.

В неподвижной жидкости затухание колебаний определялось бы величиной полного сопротивления f = kv + c. При рассматриваемом вынужденном течении в случае k < 0 происходит усиление колебаний, несмотря на то, что полное сопротивление f, конечно, положительно, и обычно велико по сравнению с вязким. Полное сопротивление f в среднем компенсировано внешней движущей силой и затухание или усиление колебаний определяется производной df/dv. Если колебания усилятся настолько, что полная скорость V = Vo+ V1 в какой-то момент станет нулевой, усиление прекратится ( кривая 4, на рис.3.27). Эксперимент также свидетельствует о том, что отрицательные абсолютные скорости пульсаций (Vo + V1 < 0) не появляются даже при очень интенсивной турбулентности; другими словами, скорости пульсаций относительно потока V1 не превышают скорости самого потока Vo .

Физически усиление колебаний можно пояснить так: дополнительная сила, возникающая из-за колебательного движения ( или приращение силы сопротивления f = f( Vo + V1) - f( Vo) всегда направлена по скорости колебательного движения и усиливает его, если f = kV + c и k < 0 (кривые 1, 1', 3,3', на рис. 3.27). В ньютоновском случае дополнительная сила направлена против скорости и тормозит колебания. Постоянная часть сопротивления "с", не зависящая от V, не влияет на колебания. Увеличение "с" лишь увеличивает стационарное растяжение пружинки l и общее сопротивление движению; при постоянном сопротивлении f = const = c колебания остаются свободными незатухающими (кривые 2, 2', на рис. 3.27). Полное сопротивление движению в твердоподобном варианте 3 (см. рис. 3.27) равно сумме большого постоянного сопротивления f3 , не влияющего на колебания, и отрицательной квазивязкости ' = df/dv < 0, усиливающей колебания. Отметим, что динамику гипотетической жидкости с отрицательной вязкостью рассматривали Яненко Н.Н. и Маслова А.Б.

Работа А усиления колебаний при < 0 ( или работа их торможения при  > 0 ) выразится интегралом: A = fdx = -  Vdt, а полное сопротивление течению возрастет из-за возмущения и генерации колебаний на величину F = A/Vt.

Если в схему рис. 3.26 ввести вместо одной две или несколько пружинок различной жесткости, то получаются, соответственно, суперпозиции двух или нескольких колебаний с разными частотами. В реальных системах, в отличие от простых случаев (см. рис. 3.27,а,б,в) , имеется множество упругих элементов с различной жёсткостью и, соответственно, не одна собственная частота колебаний, а целый спектр их. Так, собственная частота сжатия-растяжения  для столба воды длиной 1 м составляет примерно 2000 герц, так как сжимаемость воды = 5*10^-5 атм-1 . Таким же колебаниям металлической трубы соответствуют более высокие ультразвуковые частоты, а воде с 10 % пузырьков газа - низкие звуковые ; такой поток "журчит". Согласно формулe (2.2) твердоподобные сопротивления одинаково усиливают колебания по всем собственным частотам, не изменяя распределение энергии колебаний в спектре.

В реальных потоках возбуждается множество колебаний от ультразвуковых микропульсаций с частотой больше 10⁴ герц до медленных крупномасштабных автоколебаний с частотами, например, (10⁰-10^-2) герц.