3.3. Особенности на политермах и структурные перестройки в жидкости

3.3.1. Превращение в жидком железе около 1640 oС

КАК ПЕРЕХОД ОТ ПРОСТОЙ ЖИДКОСТИ К РЕАЛЬНОЙ (ЗАТВЕРДЕВАЮЩЕЙ)

К настоящему времени получено очень много данных по особенностям или аномалиям политерм вязкости сплавов на основе железа [24, 25, 112]. Часто ветвление политерм вязкости сопровождается также особенностями политерм поверхностного натяжения, магнитной восприимчивости, электросопротивления, плотности и других свойств. Неоднократно показано, что особенности политерм сопровождаются интенсивным изменением дифрактограмм расплава в том же сравнительно узком интервале температур шириной порядка нескольких десятков градусов (например, 30 К). Изменение рентгенограмм в ряде случаев истолковывается как переход при нагреве от ОЦК - подобной структуры, унаследованной от кристаллического состояния, к ГЦК - подобной, характерной для многих перегретых жидкостей. Имеются, таким образом все те признаки, по которым исследователи кристаллического состояния определяют фазовый переход в твёрдом теле [28].

Эти данные широко применяются при определении режимов термовременной обработки жидких сталей и других сплавов. Подобные превращения найдены также у ряда других переходных металлов ( у Cr, Ni, Co ) и у их сплавов, а также у алюминия и других металлов. По этим темам подготовлено порядка 100 диссертаций. Но обилие или даже "избыток" фактического материала отнюдь не приводит к ясности вопроса и нередко воспринимается теоретиками как "информационный шум", который, скорее, затрудняет понимание. Здесь ясно видно, что простое увеличение числа данных, фактов, противоречащих традиционной идеологии, отнюдь не приводит само по себе к её ломке и преобразованию.

По мнению одних авторов, превращение в жидком железе при 1640 ^оС сопровождается скачком вязкости; по мнению других, здесь наблюдается лишь излом политермы; в то же время ряд авторов вообще не находят каких-либо аномалий.

Ясно, однако, что отрицательное отношение теоретиков к этим данным связано с тем, что подобные "полиморфные превращения" в жидкости невозможны в рамках традиционной теории и поэтому воспринимаются как "противоречащие физике". Но теперь мы знаем, что в рамках этой теории вообще невозможно затвердевание; в этих вопросах традиционная модель неадекватна, поэтому нельзя на ее основе "запрещать" или "не признавать" обсуждаемые данные.

Рассмотрение с позиций предлагаемой молекулярной модели жидкости позволяет также добавить следующие аргументы в пользу обсуждаемых структурных перестроек в этих сплавах:

1) Обсуждаемые аномалии политерм и перестройки совпадают с переходом от состояния простой жидкости к непростой, то есть со вступлением расплава в интервал затвердевания.

2) Данные особенности политерм, как и многие другие, значительно яснее видны в дифференциальных координатах dln /dlnT - ln .

3) Вполне понятным становится расхождение данных различных измерений, выполненных при различных скоростях течения, так как при достаточно малых скоростях течения возможно "застудневание" жидкости и переход к качественно иным зависимостям.

Е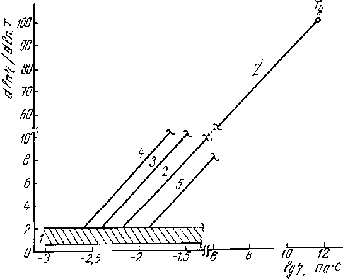 сли перенести обсуждаемые политермы (неветвящиеся) в дифференциальные координаты dln  /dlnT - ln , то вполне отчётливо выясняется различие высокотемпературных и низкотемпературных участков политермы, соответственно выше и ниже области аномалий (~ 1640 ^оС).

Рис. 3.5 Схема политерм вязкости сплавов на основе железа. Высокотемпературный отрезок (выше ~1650 ^oС) укладывается в полосу данных простой жидкости (1), низкотемпературный соответствует наклонным прямым интервала затвердевания (2-5), экстраполяция которых приводит в точку стеклования

Рис. 3.6 Политермы вязкости в дифференциальных координатах для чистого железа (1,1') и с добавками 1% ат. кремния (2), хрома (3), ванадия (4), титана (5), никеля (6), углерода (7), и 10% никеля (8), [7]. Высокотемпературные участки близки к линиям простой жидкости 1 ,11, низкотемпературные - к наклонным прямым интервала затвердевания.

Рис.3.7 Политермы вязкости в дифференциальных координатах для расплавов железа с германием, кремнием, хромом, сурьмой .

Высокотемпературный участок кривой укладывается в полосу политерм простых жидкостей, низкотемпературный - в полосу политерм интервала затвердевания (рис.3.5, 3.6, 3.7, подробнее см. [7], а также ниже).

Обычно так же выглядят в этих координатах и политермы с ветвлением, за исключением самой области аномалий (ветвления).

На высокотемпературном участке абсолютные значения вязкости с точностью 20% совпадают с компьютерными определениями и с результатами расчёта вязкости по формулам теории простой жидкости, например, по простой формуле   (m/kT)^1/2,  - поверхностное натяжение. Первая производная или температурный коэффициент вязкости dln  /dlnT не превышает 2. Вторая производная d²ln /dlnT*dln , то есть кривизна политермы, невелика, например, 0.2 - 0.5. При переходе на низкотемпературный участок (ниже области аномалий) вторая производная возрастает приблизительно на порядок величины и достигает обычных для интервала затвердевания значений около 2 - 4 или больше. Повышенное значение второй производной (то есть кривизны) на низкотемпературном участке нередко хорошо заметно и в обычных координатах - Т, однако изменение кривизны обычно не считается аномалией и не отмечается.

Многократное возрастание второй производной dln /dlnT*dln в результате превращения выявляется практически во всех случаях, когда политерма достаточно длинная, и, следовательно, определение второй производной на обоих участках становится достаточно надёжным, тенденция превышает разброс экспериментальных точек. Температурный коэффициент dln /dlnT к концу низкотемпературного участка достигает 4, 6-и, даже 8-и, если этот участок достаточно длинен, вместо 1-2 на высокотемпературном участке (значения меньше 2 соответствуют формулам теории простой жидкости).

Отклонение абсолютных значений вязкости  от величины простой жидкости приблизительно пропорционально длине Т низкотемпературного участка в квадрате и достигает заметных значений при больших Т.

В дифференциальных координатах низкотемпературный отрезок политермы выражается, согласно теории, наклонной прямой, которая "направляется" в точку стеклования (см. рис.3.5). Экспериментальные данные в целом (или в среднем) согдасуются с этой зависимостью. Экстраполяция такого отрезка даёт приблизительно координаты точки стеклования; это ещё раз показывает, что ниже 1640 ^оС расплав вступил уже в интервал затвердевания.

Чтобы не получить чрезмерный разброс точек, в дифференциальных координатах, как обычно, важно выбрать оптимальный шаг (интервал) дифференцирования Т. В ряде случаев целесообразно перейти к сглаженным экспериментальным зависимостям и принять во внимание тенденции изменения вязкости на более широких интервалах температуры Т, или усреднить группу политерм, иначе может получиться слишком большой разброс точек, намного превышающий величину выявляемых тенденций.

Часто трудно выявить изменение характера политермы около 1640 ^oС из-за того, что политермы сплавов короткие по вязкости, невелик исследуемый интервал . Качественное различие характера температурной зависимости в интервалах выше и ниже области аномалий (около 1640 ^оС) выявляется более убедительно, если не ограничиваться рассмотрением сравнительно коротких политерм, снимаемых в одном эксперименте, а принять во внимание известные тенденции изменения вязкости в широком интервале, например, на 1000 К выше и ниже области аномалий. Известно, что понижение температуры от 1640 ^оС примерно на 1000 ^оС приводит в точку стеклования сплавов, то есть изменяет вязкость приблизительно на 15 порядков величины. Однако повышение температуры на те же 1000 ^оС изменяет вязкость всего лишь на несколько десятков процентов, вместо 15 порядков на низкотемпературном участке. Хотя опытные данные высокотемпературных измерений (до 2600 ^оС) довольно скудные, уже из общих соображений ясно, что вязкость при нагреве здесь изменяется мало, в противном случае вязкость жидкого железа стала бы меньше вязкости плотного газа. Таким образом, температурная зависимость вязкости выше и ниже области аномалий действительно качественно различны (изменения вязкости - десятки процентов на интервале 1000 К выше Тп и 15 порядков величины ниже Тп).

Если измерения вязкости ведут при сравнительно больших скоростях течения, например, в вибрационном вискозиметре, то получается политерма с одним лишь скачком второй производной, то есть кривизны. Но в обычных координатах кривая со скачком кривизны воспринимается на глаз как зависимость без особенностей; даже и скачок первой производной часто не замечается визуально, если отрезки до и после скачка нелинейны. Обычно в таких случаях констатируют отсутствие особенностей; это является причиной большого числа споров о том, есть или нет особенность (аномалия) на политерме.

В целом скачок второй производной dln /dlnT*dln и переход от закономерностей простой жидкости к закономерностям интервала затвердевания на политермах, видимо, можно выявить всегда, если политерма достаточно длинная и точная. Скачок первой производной и самой вязкости, ветвление политерм выявляются, видимо, при определённых режимах измерений, нагрева и охлаждения, предыстории расплава.

При достаточно малых воздействиях на расплав он, очевидно, будет "застудневать", подобно воде, глицерину, жидкому B₂O₃ в экспериментах [119]. Можно ожидать, что при малых скоростях течения и на политермах вязкости выявится больше особенностей. Это подтверждается следующим фактом: особенностей не находят исследователи, работающие вибрационным методом, для которого характерны интенсивные механические воздействия на расплав. Такие данные получили Авалиани М. И., Каплун А. Б. [114], Гладкий В. М. [122]. Наблюдают особенности лишь исследователи, работающие методом крутильных колебаний, то есть при минимальных воздействиях и скоростях течения жидкости (V ~ 10^-1 с^-1). При этом вероятность выявления особенностей больше при малых значениях V, то есть при малых частотах, амплитуде колебаний и малом радиусе тигля. Понижая V за счёт соответствующей перенастройки прибора, можно, очевидно, обнаружить больше особенностей. Наоборот, повышая V, можно, вероятно, уменьшить, а затем свести к нулю ветвление политерм, приближаясь к данным, которые дают измерения вибрационным методом.

Не дали результата неоднократные попытки обнаружить тепловой эффект предполагаемого превращения в жидком железе около 1640 ^оС. Это, однако, вполне понятно с точки зрения предлагаемой модели. Действительно, энергия стабилизирующих структуру эффектов в модели пропорциональна энергии активации , Ucт  E, а теплота превращения U пропорциональна Е или ln. Если плавление имеет теплоту около RT и скачок вязкости около 15 порядков величины, то обсуждаемое превращение даже при большом изменении вязкости на 30 % должно сопровождаться тепловым эффектом порядка 10^-2 RT, что вряд ли доступно для измерений.

Есть мнение, что на политермах вязкости жидкого железа или алюминия на несколько сотен градусов выше обсуждаемой области аномалий выявляется ещё один скачок (или скачки) вязкости меньшей величины.