2.5.3. Диаграммы состояния других веществ в области около абсолютного нуля

У каждого вещества обычно хорошо известна температура плавления при “нормальном” давлении 1 атм, а также производная dp/dT, которая на “нормальных” участках имеет обычно величину порядка 10⁺² атм/К и положительный знак. Вид кривых плавления P_пл = f(T_пл) к настоящему времени достаточно хорошо изучен; выполняется их достаточно точная аппроксимация, в частности, с помощью формулы Симона, и уверенная экстраполяция. Так, кривая плавления гелия CD с высокой точностью описывается уравнением [13] p+17,80 = 17,311457*Т^1,5 . При охлаждении кривая плавления DС “направляется” в точку Р = -17,80 атм при Т = 0 ( штриховая кривая, рис. 2.17). Такую полную кривую мы получили бы, видимо, если бы удалось как-то избежать превращения обычного He1 в He11. Но в результате перехода жидкого гелия в состояние сверхтекучести кривая плавления резко изменяется, выходит на горизонталь АВ и приходит не в точку Р = -17,80 атм., но в точку Р=25 атм, на 42.8 атм. выше.

Кривые плавления других веществ на “нормальном” участке СD имеют такой же вид; их низкотемпературные ветви строятся экстраполяцией [101] они схематически представлены на рис. 2.17. Другие жидкости в принципе также могут охлаждаться, оставаясь в равновесии с кристаллами, вплоть до области около абсолютного нуля. Отличие их от гелия состоит в том, что для этого нужно создавать значительные отрицательные (“растягивающие”) давления. Подобные давления при

определённых предосторожностях создаются в жидкостях [102] и сравнительно легко достигаются при напряжённых состояниях кристаллического вещества. В частности, чтобы получить при абсолютном нуле жидкий водород ( Т_пл14 К), равновесный с кристаллическим, требуется не столь большое отрицательное давление порядка 1 Кбар. Трудности выхода в область около абсолютного нуля по кривой плавления не представляются непреодолимыми.

Возникает интересный вопрос: если по кривой плавления

продвинуться до температур около абсолютного нуля за счет

отрицательных давлений, то приобретут ли другие жидкости при Т0

свойства сверхтекучей квантовой жидкости ? Видимо, да; нет

оснований считать гелий исключительным веществом; его особые

свойства в этом отношении сводятся лишь к малому атомному весу и

очень слабым межатомным взаимодействиям, позволяющим получать его при Т 0 в жидком состоянии уже при положительном давлении Р= 25 атм. По сравнению с гелием Не₄² водород Н₂ имеет вдвое мень-

ший молекулярный и вчетверо меньший атомный вес, что указывает на большую величину атомарных квантовых эффектов и позволяет предполагать широкую область состояния сверхтекучей квантовой жидкости (см. рис. 2.17).

2.5.4. Подбор поправки к потенциалу для выражения эффектов, стабилизирующих структуру

Разработка квантовой молекулярной (атомарной) динамики и квантовой теории затвердевания или стабилизации атомарных структур имела бы, конечно, принципиальное значение.

Недостаточная проработка этого вопроса является в дискуссиях

одним из главных аргументов против предлагаемой модели. Но при

всей важности этой проблемы для анализа конкретных

физико-химических вопросов часто важнее представить общий

характер стабилизирующих эффектов, то есть подобрать для них

потенциал. Практически важно, например, выяснить их

дальнодействие; показать, что они коррелируют не только с

приведённой энергией взаимодействия U_вз/RT, но и с квантовым

параметром h/kT, то есть с энтропией S. Это позволяет далее

обосновать эффекты дальнодействия поверхностей, “квазикристаллические” свойства жидкости и др.

Известны программы моделирования, корректирующие по ходу

счёта парный потенциал таким образом, чтобы получить в итоге

лучшее совпадение с опытными данными. Можно этим же способом в

интервале затвердевания подбирать и корректировать и потенциал для тех стабилизирующих структуру эффектов, которые обеспечивают реальное затвердевание, отсутствующее в традиционной модели. Так как эти эффекты предотвращают или затрудняют перегруппировки атомов, то их можно заменить, в первом приближении, некоторым притяжением частиц к узлам решётки кристалла или сетки стекла. В случае жидкости назначали в ряде компьютерных экспериментов такое притяжение к узлам “V-структуры”, [11] то есть к средним положениям частиц за небольшое время усреднения. В более сложных случаях возникают вопросы: как изменяется сетка центров притяжения F_ст-сил при деформации решётки или при фазовом переходе ? В настоящее время, при разработке самых первых приближений, можно принять, что стабилизирующие эффекты F_ст одинаково придают устойчивость любой структуре, возникающей под действием обычных связей, в том числе различным решёткам, правильным и деформированным, упорядоченным и разупорядоченным структурам. В ряде случаев оказался приемлемым следующий потенциал для сил F_ст:

F_ст = к*sin(2*/d) / _ср^-3 * (0.2d-_ср),  2.1)

причём _ср =_i _i r_i^-3 / _i r_i^-3 ) (суммирование в области r_i < R)

Здесь F_ст - величина силы притяжения рассматриваемого атома к “своему” узлу решётки, который считается началом координат. При росте уклонения от узла сила F_ст притяжения атома к узлу сначала нарастает, потом убывает как sin(2/d) и затем, при  > d/2, считается нулевой; d - период решётки.

Величина _ср - среднее отклонение частиц в окружающей решетке или сетке от “своих” узлов, складывается из индивидуальных отклонений _i, причем суммирование ведется до расстояний r_i, не превышающих радиуса дальнодействия Rстабилизирующих структурных взаимодействий F_ст; многочисленные опытные данные и некоторые квантово-механические доводы свидетельствуют о том, что радиус дальнодействия R стабилизирующих структуру эффектов очень велик и имеет величину порядка коллоидного параметра L, R L1 мкм.

Опытные данные показывают, что затвердевший и упорядоченный участок структуры способствует затвердеванию других соседних участков на весьма больших расстояниях r R, причём это влияние слабо убывает с расстоянием r. Занимая определённый энергетический уровень, данная частица (фермион) “запрещает”, в соответствии с принципом Паули, переход в данное энергетическое состояние для всех других частиц системы; в этом смысле радиус дальнодействия квантовых запретов не ограничен, и это может быть физической причиной того дальнодействия стабилизирующих структуру эффектов, которое проявляется в действительности.

Величина _ср в (2.1) даёт значение среднего отклонения окружающих атомов от узлов решётки; эта величина характеризует также степень размытия структуры в монокристаллической системе, то есть при отсутствии зёрен другой ориентации, местных разупорядочений и других подобных несовершенств окружающей структуры.

Потенциал подобран так, что участки окружающей структуры, в которых среднее отклонение  > 0,2d , вносят отрицательный вклад в величину F_ст. Поэтому два монокристаллика, структуры которых не согласованы, будут согласно (2.1) отталкиваться, так как они взаимно уменьшают величину F_ст друг друга и величину энергии стабилизирующих структуру взаимодействий U_ст; между ними возникнут также дальнодействующие ориентирующие взаимодействия, приводящие их к наивыгоднейшей ориентации.

Компьютерным экспериментом можно определить величину таких

120 стабилизирующих структуру сил F_ст с потенциалом (2.1), которая обеспечит реальную стабильность решётки (сетки), например реальную механическую прочность твёрдого тела ( (10² - 10⁴ ) кГ/см²) или разумные значения энергий активации Е_V, Е_D , Е_R.

Интенсивность стабилизирующих сил F_cт приближённо оценили по величине энергии активации диффузионного скачка. В основной ячейке убрали один атом и образовали в решётке ГЦК вакансию. Соседнему атому задавали медленное равномерное перемещение в вакансию. Зависимость его энергии взаимодействия от пути по координате перескока выразилась кривой с максимумом (рис. 2.18), выражающей преодоление в ходе скачка энергетического барьера высотой Е, равной энергии активации скачка.

В другом варианте эксперимента перепрыгивающий в вакансию атом совершал свой скачок за счёт энергии исходного импульса. При варьировании интенсивности стабилизирующих структуру сил F_ст энергия активации скачка E_ск/U_реш изменялась следующим образом:

F_ст/f_парн 0,10 0,20 0,40 0,60 ;

E_ск/U_реш 0,15 0,27 0,51 0,75 .

Из этих данных видно, что реальная величина энергии активации скачка в модели Е_ск ≈U_реш/4 получается при величине стабилизирующих сил F_ст ≈0,18*f_парн,, где f_парн - величина обычных парных сил притяжения или отталкивания, действующих на атом от всех соседей при равновесии решётки. Для аргона f_парн≈12* d/dr6*10^-4 дин при r=r₀. Следовательно, для создания реальной жёсткости и стабильности решётки в модели требуются стабилизирующие силы, приблизительно на порядок величины меньшие по сравнению с обычными силами связи f_парн.

Это согласуется с тем фактом, что теплота затвердевания и

теплота плавления составляет обычно около 1/10 энергии решётки.

Стабилизирующая поправочная добавка F_ст величиной около 1/10 энергии решётки приводит также к разумным значениям предела прочности твёрдого тела [7]. Можно надеяться, что с помощью подобного потенциала удастся описать и ряд других свойств твёрдых тел *).

______________________________________________________________________

*) Была сделана также попытка получить подобные (2.1) стабилизирующие взаимодействия как компоненту при квантовом расчете энергии связи, то есть не из атомарных, а из электронных квантовых эффектов [22].

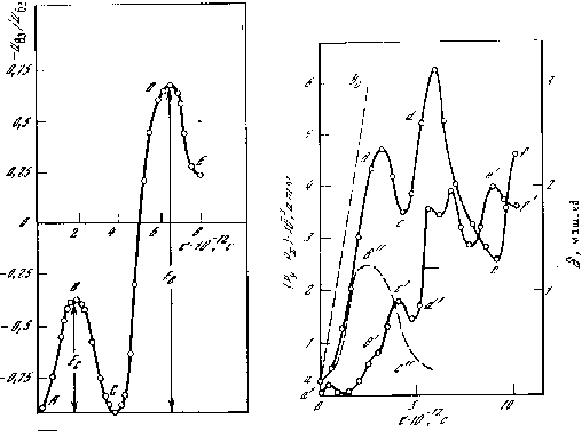
Рис. 2.18. Определение энергии активации диффузионного скачка в компьютерном эксперименте. На интервале АВС атом совершает скачок в вакансию, а на следующем интервале СДЕ - в занятый узел, выталкивая атом, находившийся там ранее. Еа - энергия активации скачка в вакансию, Еб - в занятый узел

Рис. 2.19. Определение предела прочности в машином эксперименте. Моделируется сдвиговая деформация с постоянной скоростью v=2*1011 c-1; на участке аб напряжения (Рy-Рx) нарастают приблизительно в соответствии с законом Гука (прямая аб), затем наступает релаксация, сопровождаемая ростом диффузионного смещения атомов (участок вс); кривая авс получена при учёте зависимости Fст от  и Sвз