2.3.2. Устойчивость решеток и сеток

Возможности компьютерного моделирования в молекулярных моделях часто лимитируются экономичностью программ, которую не может заменить даже использование суперкомпьютеров; часто успех определяется тем, насколько экономична разработанная программа. В этом отношении предпочтительнее моделировать не вязкое или пластическое течение вещества, а лишь один элемент этого течения, выражающий физическую сущность процесса - релаксацию механических напряжений. Далее, эту релаксацию целесообразно выполнять при температурах около абсолютного нуля, то есть с помощью релаксационной процедуры, так как в этом варианте машинное время не тратится на обсчет тепловых колебаний, а в системе развиваются лишь направленные перемещения частиц, выражающие молекулярный механизм релаксации напряжений. Следующий шаг в повышении экономичности программы состоит в том, чтобы не моделировать весь процесс релаксации напряжений, а лишь выяснять - пойдёт ли этот процесс? Для этого достаточно выяснить - устойчиво ли исходное состояние? Будут ли малые отклонения от равновесия в исходном состоянии лишь уменьшаться, или же некоторые компоненты этого отклонения будут самопроизвольно увеличиваться, свидетельствуя о неустойчивости системы? Если провести счёт до конца, то увеличивающиеся уклонения от равновесия приведут к расплыванию всей исходной структуры, к возникновению новой структуры с релаксацией напряжений. В связи с этим были поставлены компьютерные эксперименты также по определению устойчивости атомных решеток и сеток, по определению их спектров колебаний и мягких мод, свидетельствующих о пониженной устойчивости по отношению к определенным перегруппировкам частиц.

Устойчивость часто объясняют на примере простейшей механической системы - шарика в ямке или материальной точки в потенциальной яме. Устойчивостью D* называют вторую производную d²U/dr², или кривизну ямы. Эту величину называют также жёсткостью связи; она характеризует и частоту  колебаний частицы в яме: = (D*/m)^1/2, частота равна (D*)^1/2, если масса единична.

Примером абсолютно неустойчивой системы является “шарик на горке” или частица в точке максимума энергии, когда d²U/dx² < 0. В такой системе случайно возникшие отклонения от точки равновесия самопроизвольно нарастают.

Аналогично, термодинамической устойчивостью системы D* по параметру х обычно называют [84] величину второй производной d²U/dx² или d²F/dx², где U - энергия, F - свободная энергия. Если одновременно могут изменяться несколько параметров x₁, x₂..., то величина устойчивости определяется детерминантом, составленным из вторых производных энергии U или F по параметрам x₁, x₂... Термодинамическая устойчивость стремится к нулю с приближением жидкости к критической точке. Устойчивость сжатого пара или “растянутой” жидкости убывает по мере отклонения от равновесного давления, затем становится нулевой и отрицательной. Такой “ абсолютно неустойчивый” пар быстро распадается на две фазы: здесь D* = d²F/dV² =-dp/dv < 0, так как dp/dv > 0. Как отмечено выше, абсолютно неустойчивым оказывается в модели “стержень” из леннард-джонсовских частиц с деформацией сдвига 11 % и больше; для такой системы d/d<0. При деформациях (8-11) % устойчивость такой деформированной решетки положительная, но очень малая; ускоряющаяся релаксация напряжений вызывается небольшим исходным возмущением системы.

Устойчивость молекулярной системы многих частиц можно истолковать таким же образом, как и устойчивость одной частицы в яме, но вместо “шарика” можно говорить о фигуративной точке системы в конфигуративном 3N-мерном пространстве; а вместо координаты х - об 3N-мерном вектореR с компонентами x₁₁, x₁₂,...x_3N, причём R² = x₁₁² + x₁₂² ...x_3N² есть величина диффузионного смещения частиц, которая определяется обычно программой компьютерного эксперимента для расчёта коэффициента диффузии D: R² = 6DtN + const.

Вместо одной величины жёсткости связи и одной частоты нужно рассматривать спектр из 3N значений этих величин. Наиболее интересны для нас минимальные значения , D*; они соответствуют движению фигуративной точки системы от 3N-мерного минимума энергии или от “дна” 3N-мерной потенциальной ямы по линии наиболее пологого подъёма по самой пологой “энергетической ложбине” на энергетической поверхности U= U(x₁₁,x₁₂,...x_3N).

Перегруппировки групп из n частиц, соответствующие элементарным актам вязкого (пластического) течения, диффузии, электропроводности и др., а также элементарным актам фазовых переходов, соответствуют перемещениям фигуративной точки в 3n-мерном пространстве по координатам с минимальными значениями . Максимальные частоты  соответствуют дебаевской температуре D=h/k и отвечают обычным тепловым колебаниям.

Энергия активации Е каждой перегруппировки при прочих равных условиях пропорциональна устойчивости по соответствующей координате, D*=(d²U/dx²), и величине смещения х данной перегруппировки в квадрате: E~D*x². Связь энергии активации Е с устойчивостью и частотой представлена на схеме рис.2.15.

Е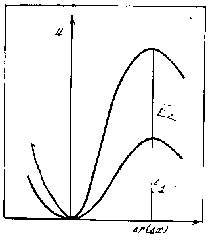 сли на структуру наложены механические напряжения , то её устойчивость к перегруппировкам понижается. При абсолютном нуле температуры предел прочности п- это та величина напряжений  , при которой устойчивость к течению или релаксации напряжений становится нулевой. При конечной температуре Т небольшие энергетические барьеры Е могут преодолеваться активационно, с вероятностью exp(-E/RT), и предел прочности п- это та величина напряжений , которая понижает устойчивость до малой величины, когда Е не превышает нескольких величин RT, и множитель exp(E/RT) не очень сильно отличается от единицы.

Рис.2.15 Схема, поясняющая пропорциональность энергии активации Е и устойчивости D* ( или кривизны графика энергетической потенциальной ямы)

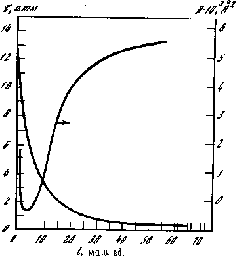
Рис. 2.16 Изменение cуммарного квадратичного смещения частиц D по ходу релаксации напряжений: = 10%, периодические граничные условия

Таким образом, стабильность структуры к перегруппировкам частиц, которая является основной величиной, обсуждаемой в этой книге, есть механическая устойчивость структуры в длинноволновой части спектра. Мерою этой стабильности, наряду с энергиями активации Е, могут быть величины D*, . Вязкое течение, диффузия, фазовые переходы идут через наиболее легкие из различных возможных перегруппировок, соответствующих мягким модам спектра с минимальными частотами. Известно, что с приближением к температуре фазового перехода в спектре появляется соответствующая мягкая мода.

Чтобы показать, что структура в традиционной модели не затвердевает, достаточно показать, что в её спектре есть достаточно низкие частоты, более мягкие моды, чем, например, в дебаевском спектре или в спектре реального твёрдого тела. Стабилизирующая структуру добавка Fст к взаимодействию должна привести к исчезновению этих мягких мод.

Практически устойчивость структур в компьютерных экспериментах легко определяется по времени восстановления равновесия системы, в которую внесено возмущение в виде небольших отклонений частиц от узлов. При установившемся равновесии компьютер выдает одинаковые, не меняющиеся со временем значения всех рассчитываемых величин - энергии, компонент давления, координат частиц и др. При заданной точности счета, например, до 7-й значащей цифры, процесс прекращается. Если же предел устойчивости решетки превышен, то за некоторое время Т_У устанавливается самопроизвольно ускоряющийся процесс релаксации напряжений. В определениях устойчивости деформированной решетки леннард-джонсовских частиц время Т_У установления равновесия (или релаксации) было следующим:

Величина деформации,,%	0	1	5	9	10	10,5	10,55	10,60	11	15
Время Ту, шагов счета	90	110	210	430	940	1650	7800	3400	1200	60

Отсюда видно, что предел устойчивости системы соответствует примерно деформации 10.55%; при этой нагрузке полного равновесия не удалось получить даже после 7800 шагов счета. Вдали от предела устойчивости сравнительно быстро устанавливается либо ускоряющаяся релаксация напряжений (за 60 шагов при 15%), либо равновесие (за 90 шагов при нулевой нагрузке). Деформация на 10.55% понижает устойчивость D*~1/Tу решетки примерно в 100 раз.

Перегруппировка частиц, соответствующая релаксации напряжений, при деформации выше 10.55% становится абсолютно безактивационной; фигуративная точка системы лишь опускается в 3N-мерной энергетической ложбине; энергия лишь понижается. Устойчивость по этой степени свободы отрицательная, около =10.55% почти нулевая, к 15% - большая по абсолютной величине отрицательная устойчивость. Исходная система соответствует “шарику на горке”, причем энергетическая “горка” достаточно крутая при 15% и очень пологая при  = 10.6%. Около 10.55% “горка” становится “равниной”, а при меньших нагрузках на пути релаксации напряжений появляется сначала небольшой, а затем значительный подъем с общей высотой энергетического барьера Е до Е  2RTпл при нулевой нагрузке.