2.3. Кристаллизация. Устойчивость

2.3.1. Моделирование кристаллизации

По обычным представлениям, традиционная модель жидкости и твёрдого тела имеет кинетические свойства реальных веществ, и процессы кристаллизации в ней должны протекать приблизительно с такими же скоростями, как и в действительности. Наоборот, согласно концепции, предлагаемой в данной книге, процессы упорядочения или кристаллизации должны протекать безактивационно и значительно быстрее, чем в действительности при всех температурах, и особенно около абсолютного нуля; безактивационное упорядочение должно проходить за время, по порядку величины примерно соответствующее периоду колебаний атома.

Реальные процессы кристаллизации, как известно, протекают довольно трудно и медленно, сопровождаются преодолением высоких энергетических барьеров; энергия активации процесса кристаллизации часто имеет величину порядка 20 RTпл.

Скорость кристаллизации Vк в зависимости от температуры описывается кривой с максимумом, который приходится на температуры примерно (0,8 - 0,9) Тпл; при дальнейшем понижении температуры Vк экспоненциально убывает. Наибольшие линейные скорости продвижения фронта кристаллизации наблюдаются у металлов; скорость Vк в точке максимума достигает величин порядка 10¹ см/с и даже 10² см/с. У вязких силикатных расплавов максимальная скорость часто имеет порядок 10^-2 - 10^-4 см/с [10, 81, 82]. Время полной кристаллизации жидкости определяется не только линейной скоростью продвижения фронта кристаллизации Vк, но ещё и вероятностью появления зародышей кристаллической фазы. Минимальные значения времени кристаллизации, с которыми сталкиваются при стекловании металлов, имеют величину порядка 10^-3 с или несколько меньше. У вязких силикатных расплавов минимальное время кристаллизации может составлять несколько минут или несколько часов [10, 81, 82].

При охлаждении время кристаллизации быстро растёт и затем выходит за пределы возможностей измерения. Уже в точке стеклования оно имеет макроскопическую величину, например, 1 час, а при Т  Tст/2 достигает нескольких лет и более.

Кристаллизацию или упорядочение моделировали при температуре около абсолютного нуля, T  0, где расхождение традиционной и предлагаемой моделей наибольшее. Весьма полезны при этом оператора вида X:=X*(1+Pxx /n), позволяющие поддерживать в системе постоянное давление при изменяющемся объёме. Реальная кристаллизация сопровождается изменением объёма на несколько процентов, а при неизменном объёме возникают очень большие давления, например, 10⁵ атм. Это затрудняет моделирование кристаллизации при обычных периодических граничных условиях, когда объём постоянный.

Исходную плотную аморфную структуру получали либо переохлаждением жидкости в модели, либо сжатием системы с хаотическим распределением частиц, задаваемым с помощью генератора случайных чисел.

На рис. 2.10, 2.11 представлены последовательные стадии упорядочения в плоской системе леннард-джонсовских частиц; изображены ячейки структуры и многогранники (многоугольники) Вороного частиц. Процесс идёт очень быстро, и к 350 -му шагу уже образовалась практически идеальная плоская упаковка с тремя вакансиями. 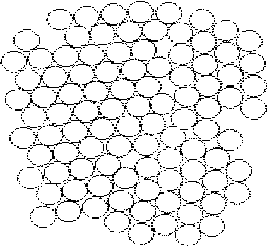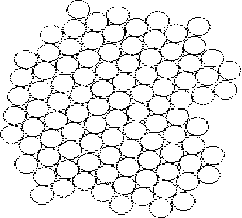Соответственно выросли максимумы на функциях радиального и углового распределения частиц [7]; рост максимумов выражает переход к более правильной структуре. На рис. 2.12 представлен подобный процесс при обычном изображении атомов Ar кружками. Рис. 2.12, а - соответствует газовой хаотической структуре, б - жидкостной, к концу процесса достигается практически идеально правильная “решетка” (рис. 2.12, г). Правильная огранка “кристаллика” в подобных экспериментах не получается, и, по видимому, ее получить невозможно.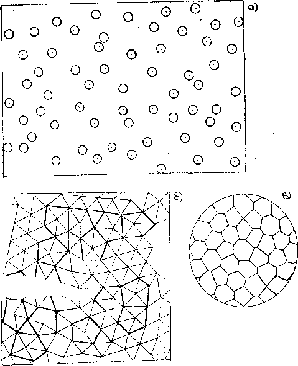

Рис. 2.10. Упорядочивающаяся структура (а,б) и её многогранники Вороного (в). Упорядочение сводится к переходу семи- и пятиугольников Вороного в правильные шестиугольники

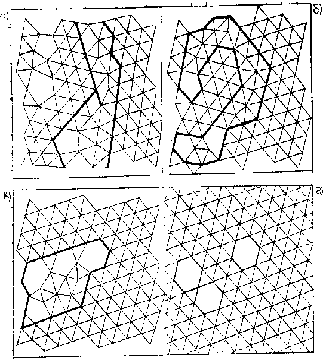
Рис. 2.11. Последовательные стадии упорядочения в системе леннард-джонсовских частиц; изображены ячейки структуры (а - в). К 350 - му шагу образовалась практически правильная плоская решётка с тремя вакансиями (г)

Аналогично протекает упорядочение и в объемной системе, однако в этом случае нет столь наглядного его изображения; за упорядочением приходится следить по таким показателям, как функции радиального распределения или гистограммы многогранников Вороного. Отметим, что в модели наблюдалась не только кристаллизация или упорядочение, но и столь же быстрая рекристаллизация - рост одной области упорядочения за счёт уменьшения другой со скоростью порядка скорости теплового движения. В реальных системах эти процессы также практически не идут при низких температурах.

Моделировали аналогичный процесс упорядочения в объёмной системе 10*10*10/2=500 частиц с потенциалом 6 - 12. Максимумы функции радиального и углового распределения частиц возрастали качественно так же, как и при упорядочении плоской системы. Соответственно возрастали энергия и плотность. “Кристаллизация” в объемной системе идет, очевидно, качественно так же, как и в плоской.

Моделировали упорядочение в плоской структуре с кулоновским взаимодействием, потенциал 1 - 10 . В случае системы 98 частиц периодические граничные условия не соответствуют решётке NaCl. Видимо, по этой причине идеальная решётка не была достигнута к 1700 -му шагу счёта; структура имела довольно высокую степень упорядочения, но содержала дефекты типа вакансий и “разбавленного беспорядка” [84] (рис.2.13).

а) б)

в) г)

Рис.2.12 Упорядочение при обычном изображении атомов Ar кружками: а-хаотическая газовая структура, б-жидкостная, г-практически идеальная “кристаллическая решетка”

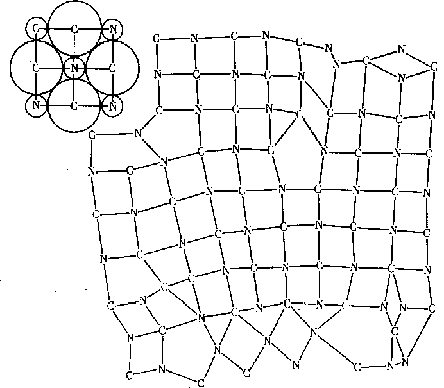
Рис.2.13. Упорядочение позиционное и по сорту атомов из случайного исходного размещения

В системах с тенденцией к расслоению, когда взаимодействие одноимённых частиц больше, чем разноимённых, образовались кластеры чистых веществ А и В, содержащие порядка 10 частиц одного сорта (рис. 2.14).

Моделирование вязкого течения и релаксации напряжений показало, что в традиционной молекулярной модели нет затвердевания. К такому же выводу приводит и моделирование кристаллизации или упорядочения.

В реальных системах кристаллизация идёт с преодолением высоких энергетических барьеров и требует большого времени, например 1 год, уже при охлаждении до температуры Тст/2. В модели она идёт безактивационно и даже при Т  0 практически заканчивается за 10^-10 - 10^-12 с.

При моделировании течения или релаксации напряжений требуются значительные усилия для обеспечения равенства движущих сил процесса в модели и в действительности. При моделировании упорядочения это условие выполняется автоматически: движущая сила в обоих случаях равна работе упорядочения. Здесь нет даже таких отдаленных аналогий или некоторых общих элементов в поведении модели и реального вещества, которые наблюдаются в определениях прочности в случае идеальных монокристаллических решеток. Поведение модели резко, качественно отличается от поведения реальных веществ; после осознания этого факта появляется удивление - каким образом удается не замечать это разительное отличие. Чтобы понять это, нужно принять во внимание особую психологию научного исследования в период “кризисов”.

Столь же легко и быстро идут в модели процессы упорядочения частиц по сорту, “полиморфные превращения”, расслоение, образование и “залечивание” пустот, рекристаллизациия и др. Во всех случаях в модели процесс протекает наиболее быстро при температурах около абсолютного нуля. Трудности моделирования наступают лишь в случае таких структурных перестроек, когда частицы должны перемещаться на сравнительно большие расстояния, например, на 5 диаметров; здесь мы приближаемся уже к пределу возможностей обычных компьютеров и программ.

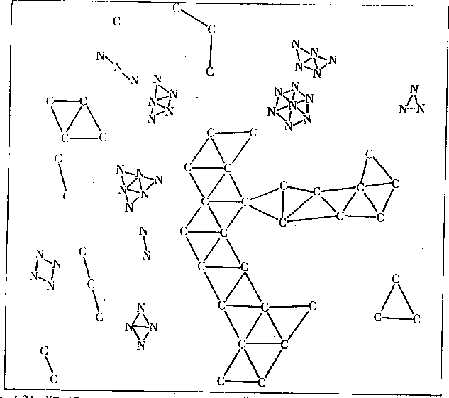
Рис. 2.14 Упорядочение при тенденции к расслоению раствора.

Молекулярный механизм упорядочения в модели также не похож на механизм реальной кристаллизации. Действительная кристаллизация идёт, как известно, как гетерогенный процесс, с редким и трудным появлением зародышей и их последующим ростом, который часто идёт ещё скачками, “квантами” или присоединением и ростом двумерных зародышей. В модели же упорядочение идёт скорее гомогенно, на всех участках структуры одновременно. Если построить многоугольники ( в объёме - многогранники ) Вороного, выделяющие ячейку каждой частицы, то упорядочение на плоскости сведётся к преобразованию семи- и пятиугольников, характерных для аморфной структуры, сначала в неправильные, а затем в правильные равносторонние шестиугольники, см.стр. 90, рис.2.8 "в". В процессе упорядочения такую эволюцию проходят одновременно почти все ячейки структуры. У семиугольных ячеек постепенно сокращается одна из сторон, пока не исчезнет. У пятиугольников одна сторона растёт до тех пор, пока не появится излом, делящий её на две стороны. Почти правильные шестиугольники, то есть ячейки кристаллической структуры, появляются в аморфной структуре поодиночке и небольшими группами. Лёгкое появление столь малых “зародышей” кристаллической фазы свидетельствует также о том, что на границе упорядоченной и неупорядоченной структуры в модели практически нет поверхностного натяжения; эти структуры смешиваются в разных пропорциях и “взаиморастворяются”. Но чтобы наблюдать равновесный раствор “кристаллических” и “жидкостных” ячеек структуры, нужно провести моделирование около температуры плавления.

В объёмной системе кристаллизация идёт в модели приблизительно так же, но её труднее наглядно представить на рисунке.