2.2.3. Молекулярный механизм пластической деформации или вязкого течения

При деформации реальных твёрдых тел в течении участвуют, как известно, лишь немногие молекулы или атомы. При растяжении монокристалла течение часто сосредоточивается в одной атомарной плоскости - "плоскости скольжения" [12]. Течение может свестись к перемещению всего лишь одной краевой дислокации; все остальные атомы могут находиться у "своих" узлов решётки и не участвовать в течении. Если нагружать пластинку хрупкого материала, например стекла, на изгиб, то наступает быстрое хрупкое разрушение практически без пластической деформации, путём распространения хрупкой трещины. При ударе подобным образом разрушается даже струя жидкости [80]. Обычно считается, что традиционная модель передаёт основные особенности затвердевания, а, значит, и отмеченные механизмы деформации и разрушения. Компьютерные эксперименты не подтверждают и это следствие обычных взглядов.

Если у реальных твёрдых тел течение идёт за счёт активационных перескоков немногих атомов, решётка сохраняется, то в компьютер-ной модели идеальная исходная решётка быстро расплывается, и течение идёт за счёт дрейфа практически всех атомов (см. рис.2.1, рис.2.5). На последующих стадиях деформации образуются небольшие участки упорядоченной структуры, которые затем тоже расплываются, и т.д.. В такой системе невозможно и хрупкое разрушение без деформации; система ведёт себя как растягиваемый образец жидкости. Даже когда целью экспериментов является моделирование распространения хрупкой трещины [8], в модели получается глубокая деформация образца и высокая пластичность; относительное удлинение образца Ar или NaCl до разрыва, которым характеризуют хрупкость, в модели часто превышает удлинение наиболее пластичных реальных материалов, и даже удлинение специальных "сверхпластичных" сплавов с рекордными показателями пластичности. Это вполне понятно, если учесть, что "вещество" в модели имеет механические свойства плотного газа или простой жидкости. Практически "стержень" в модели растягивается, даже при Т  0, как "нить" или струя жидкости. Чтобы получить в модели реальное поведение хрупкого твёрдого вещества, нужно как-то "скрепить", стабилизировать его решётку, чтобы она не расплывалась, а разрушалась при нагружении. Реальные решетки являются весьма жесткими; при низких температурах и быстрых воздействиях они способны практически лишь к хрупкому разрушению. В компьютерной модели даже при Т  0 и огромных скоростях деформации (10¹⁰ c^-1 и больше) наблюдается быстрое расплывание или аморфизация структуры, обратная "кристал-лизация", рост одних зерен за счет других ("рекристаллизация"), растворение одних атомных плоскостей и цепочек и образование других и т.д. Такую текучесть структуры особенно удобно "непосредственно наблюдать" в случае плоских систем при выведении графического изображения структуры на мониторе компьютера.

2.2.4. Молекулярный механизм течения около абсолютного нуля

В реальных твёрдых телах при течении сохраняется решетка или сетка, течение идёт за счёт активированных перескоков частиц, вызывающих перемещение вакансий, дислокаций и др. При Т  0 вещество становится хрупким, течение практически прекращается, лишь одна часть решётки (сетки) может оторваться от другой при хрупком разрушении. Совершенно иной механизм течения наблюдается в модели.

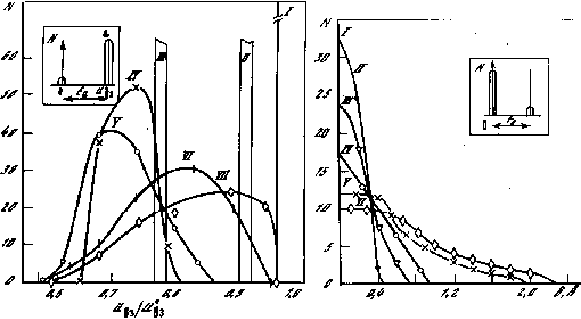
Рис.2.6 Распределение частиц по энергиям на разных стадиях деформации 1-8. Видно, что находятся в необычном энергетическом состоянии и принимают участие в течении многие или почти все частицы. Вверху - распределение при активационном течении

Рис.2.7 Распределение частиц по смещениям. Видно, что смещаются и участвуют в течении почти все частицы. Вверху - то же распределение при активационном механизме

Нет надежды получить здесь хрупкое разрушение. Структура текуча, правильная решётка легко расплывается или перестраивается в другую, почти правильную, решётку. При растяжении образца он не разрушается, как в хрупком состоянии, а растягивается и утоньшается, как нить вязкой жидкости; это наблюдается как при обычных граничных условиях, так и при свободных поверхностях.

Для уточнения механизма процессов программой было предусмотрено построение гистограмм величины смещений частиц от "своего " узла решётки и их энергий (рис. 2.6, 2.7).

Из гистограмм видно, что механизм процесса не похож на активационный. При активационном механизме основная часть частиц остаётся около своих узлов и сохраняет неизменную энергию взаимодействия; лишь немногие частицы (активированные) смещаются на расстояние, примерно равное периоду решётки, и повышают энергию на dЕV. Так, в точке 2 рис. 2.2 напряжения вдвое меньше величины  , соответствующей закону Гука, которая была бы при правильной упруго деформированной решётке; к этому моменту уже прошло, следовательно, уменьшение напряжений  вдвое, прошла " двукратная релаксация". Между тем максимальное смещение атома от узла решётки составило лишь 0,1r ( при активационном механизме было бы r ), а среднее смещение - лишь 0,02r . Почти одинаковыми остались и энергии взаимодействия всех частиц. В модели происходит большая релаксация напряжений или значительная деформация при очень небольших смещениях, но почти всех частиц и небольших изменениях энергии. Десятикратная релаксация достигается при наибольшем смещении ~ 0,3r, стократная - при  ~ 0,5r и др.

Механизм перемещения частиц в модели подробен дрейфовому, при котором дрейфуют, плывут все частицы. Чтобы получить активационное движение и хрупкое разрушение, необходимо как-то укрепить,стабилизировать структуру, затруднить её расплывание и перегруппировки частиц.

Отметим, что механизм перемещений получается несколько различным в зависимости от того, совпадает ли направление плотно упакованных цепочек частиц в решётке с направлением растяжения или сжатия.

Характерная особенность механизма течения - это образование и расплывание, рост на одних участках и убывание на других участках областей упорядоченной структуры - "кластеров", процессы аморфизации на одних участках и упорядочения на других. При сравнительно малых скоростях деформации v = (10⁷ - 10⁸) с^-1 доля аморфизированной структуры становится незначительной, одна упорядоченная структура почти непосредственно переходит в другую упорядоченную ( подробнее см. [7]). Текучесть атомарной структуры в модели Ar (даже при Т  0) отчетливо проявляется также при моделировании слияния малых сферических монокристалликов (рис. 2.8) и при моделировании "затекания" исходной сферической полости в монокристаллике (рис. 2.9). Здесь также видны процессы разупорядочения, упорядочения, "рекристаллизации" - роста одних кластеров или упорядоченных участков за счет других. К концу процесса (примерно к 3000-му шагу) в oбоих случаях достигается почти идеально правильная "кристаллическая структура" вновь возникших образований. Реальные структуры не проявляют подобной текучести и способности к перестройкам; образцы реальных веществ в подобных условиях дают либо хрупкое разрушение при больших нагрузках, либо остаются неизменными при малых.

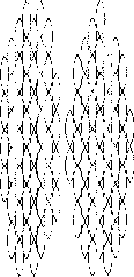
Рис.2.8. Слияние сферических монокристалликов при T ≈ 0.

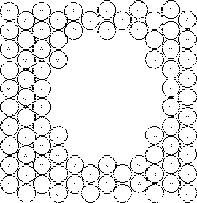
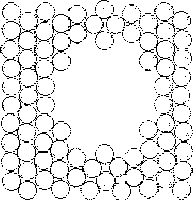
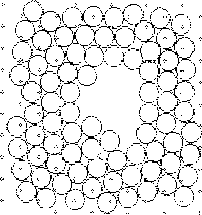
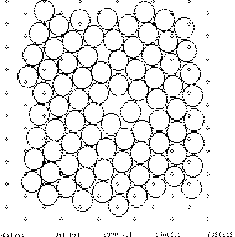
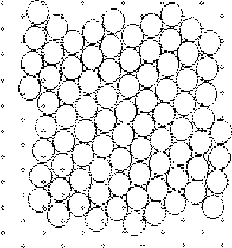
Рис. 2.9 “Затекание”(а, б, в, г) полости в микрокристаллике, Т = 0. К 3000-му шагу достигается практически правильная “кристаллическая решетка” вновь возникшего образца, рис. 2.9 д.