2.1.3. Течение в модели при температурах около абсолютного нуля

Интересно выяснить поведение традиционной модели при Т  0, то есть при "предельном затвердевании". Практически условие Т 0 реализуется тем, что скорости всех частиц зануляются в конце каждого шага, как в работах [73, 74] и др.; это соответствует переходу к релаксационной процедуре. Смещение по данной координате х за шаг при нулевой начальной скорости пропорционально действующей силе f_x: x = fx*t²/2m. Изображающая точка системы в координатном 3N - мерном фазовом пространстве перемещается к точке минимума энергии, то есть ко дну 3N - мерной потенциальной ямы или к точке равновесия, где U(х1,х2,...x3N) = min, по линии наиболее крутого спуска. В этом варианте компьютерного эксперимента могут идти лишь полностью безактивационные перегруппировки частиц; действительно, при релаксационной процедуре изображающая точка движется только в сторону понижения энергии U (роста энергии взаимодействия Uвз); активация ( рост U) невозможна. В этом варианте нет тепловых колебаний частиц и флюктуаций вычисляемых величин. Происходят лишь направленные перемещения частиц, соответствующие механизму течения. Механизм процессов выявляется наиболее ясно, не затемняется тепловыми колебаниями частиц. Если компьютер выдает результаты, например, с 7 значащими цифрами, то даже изменения в последней значащей цифре являются "физическими", несут информацию о механизме и темпе процесса атомарных перегруппировок. При обычном моделировании скорость случайного теплового движения значительна, изменения даже первой или второй значащих цифр каждого результата могут отражать не направленное протекание процесса, а только лишь случайные тепловые колебания рассчитываемой величины.

Таблица 2.1. Результаты определения кинетических коэффициентов вязкости , диффузии D, электропроводности  ниже точки плавления методом молекулярной динамики

п/п	Вещество	Потенциал	Т/Тпл	, сПз	D*105,см2/с	, ом-1см-1
1	Ar	6 - 12	0,24	5,3	0,53	-
2	Ar	6 - 12	0,24	4,2	0,46	-
3	Ar	6 - 12	1,20	0,35	0,57	-
4	Ar	4 - 8	0,12	0,13	0,10	-
5	NaCl	1 - 10	0,42	9,40	-	-
6	Pb	Осцил.	0,40	8,60	4,20	-
7	Fe	Осцил.	0,40	7,40	3,40	-
8	Оксид	Ион-ков.	0,40	5,00	-	--
9	Ar	6 - 12	0,24	6,00	-	-
10	Ar	6 - 12	1,40	0,32	-	-
11	Ar	4 - 8	0,24	0,10	-	-
12	Ar	Ж. сферы	0,24	0,15	-	-
13	Ar	6 - 12	0,24	3,40	0,39	-
14	Ar	6 - 12	0,80	2,40	0,73	-
15	Ar	6 - 12	0,24	3,70	0,67	-
16	NaCl	1 - 10	0,23	-	15,00	0,80
17	NaCl	1 - 10	0,23	-	8,00	1,40
18	NaCl	1 - 10	0,60	-	-	3,00
19	NaCl	1 - 10	0,60	-	-	0,20
20	Оксид	Ион-ков.	0,40	-	6,00	2,40
21	Оксид	1 - 10	0,60	-	2,00	0,23
22	Оксид	6 - 12	0,24	1,40	-	-

Продолжение таблицы 2.1. Параметры моделируемых процессов

N п/п	Моделируемый процесс	Скорость V, c-1	Напряжённость поля , B/см
1	Вязкое течение	4,9*107	-
2	Вязкое течение	4,9*108	-
3	Вязкое течение	6,9*109	-
4	Вязкое течение	6,9*109	-
5	Вязкое течение	4,0*109	-
6	Вязкое течение	4,0*108	-
7	Вязкое течение	4,0*108	-
8	Вязкое течение	4,0*108	-
9	Течение при Р=1400 кгс/см2	-	-
10	Течение при Р=1400 кгс/см2	-	-
11	Течение при Р=1400 кгс/см2, "выключенном" притяжении	-	-
12	Течение при Р=1400 кгс/см2 потенциал ж. cфер	-	-
13	Релаксация напряжений	-	-
14	Релаксация напряжений	-	-
15	Релаксация формы	-	-
16	Электроперенос	-	6,2*106
17	Электроперенос		6,2*107
18	Электроперенос		6,2*107
19	Электроперенос		2,0*109
20	Электроперенос		6,2*106
21	Плоскость, электроперенос		6,2*107
22	Плоскость, вязкое течение	3,0*1010	-

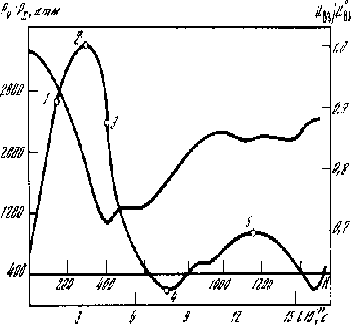
Рис. 2.1. Зависимость напряжений сдвига Рx-Рy и энергии Uвз от времени деформации, или от числа шагов N

Таблица 2.2. Коэффициенты вязкости и диффузии при моделировании

деформации плоской и объёмной систем ( 98 и 108 частиц ); Т=0.

No	Система	, с-1	п	/Tпл	уп, Пз	ср, Пз
1	Пл.	2,5*1010	2	0	2	-
2	Пл.	3,1*109	0,65	0	1,4	0,2
3	Пл.	5,8*108	0,13	0	1,1	0,6
4	Пл.	3,1*109	0,05	0	0	-
5	Об.	4,1*109	0,35	0	-	0,12
6	Об.	4,1*108	0,05	0	1,1	0,6
7	Об.	4,3*107	0,007	0	-	-
8	Пл.	6*108	0,07	0	-	0,23
9	Пл.	4*1010	1,0	0,5	0	-
10	Пл	4*1010	0,6	0,5	0	-
11	Об.	4*1010	1,0	0,25	0,04	0,01

Продолжение таблицы 2.2

No	Dуп*105, см2/с	Dср*105,см2/с	max/G	ср/G	UвзUoвз
1	4	110	0,12	0,04	-
2	6	30	0,07	0,025	0,74
3	6	8	0,02	0,015	0,91
4	5	-	-0,006	-0,003	0,79
5	-	20	0,016	0,011	0,86
6	-	16	0,009	0,005	0,96
7	7	-	2*10-4	1,1*10-4	1,0
8	-	9	-	0,008	-
9	-	100	3*10-3	-	-
10	-	200	0,01	0,06	-
11	-	250	0,032	0,015	-

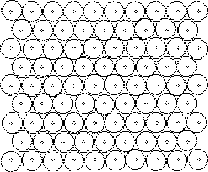
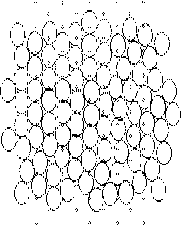
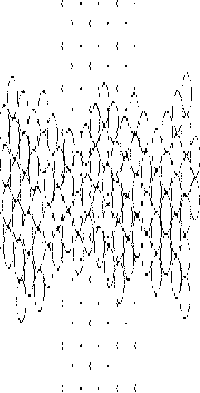
Рис. 2.2 Изменение структуры при деформации в плоской системе. Потенциал 6-12, Т ~ 0. Нет признаков хрупкого разрушения; видны образующиеся по ходу деформации вторичные местные упорядочения ("кластеры")

Рассмотрим подробно один из компьютерных экспериментов (рис. 2.2). Исходная система - идеальная плоская плотная упаковка частиц. Система растягивается "силовым полем" по ребру Х и сжимается по ребру У. При деформации протекают два конкурирующих процесса: вследствие роста степени деформации на d за время dt упругие напряжения возрастают на dt =Gd , где G - модуль сдвиговой упругости. С другой стороны, происходит релаксация напряжений, которую описывает формула Максвелла:

 = _O*exp(-Gt/) = _O*exp(-t/Tr).

Здесь  - искомая (определяемая) динамическая вязкость, Tr=/G - время релаксации. На первой стадии процесса до точки 1 рис. 2.1 идёт почти упругая деформация, напряжения сдвига возрастают почти по закону Гука, релаксация напряжений молозаметна. В точке 2, где напряжения максимальны, скорость релаксации напряжений сравнивается со скоростью их роста по закону Гука. Затем до точки 4 релаксация напряжений обгоняет их рост вследствие деформации. Получаются следующие мгновенные значения вязкости на разных стадиях процесса: точка1 на рис. 2.1., упорядоченная структура - 1,4 дПа*с; точка 2, переходная структура - 0,4; 3, аморфная структура - 0,1; 4,5 -смешанные структуры, 0,02 и 0,15 дПа*с . На стадии упорядоченной структуры ( точка 1) вязкость получается на 1- 2 порядка величины больше, чем на стадии аморфной структуры в точках 3,4. Коэффициент самодиффузии на стадии упорядоченной структуры cоставлял 4*10^-4 , а на стадии аморфной - 11*10^-4 см²/с.

Энергия взаимодействия убывает вследствие деформации и возрастает вследствие релаксации напряжений; сначала примерно до точки 2 преобладает первый процесс, затем - второй. Основные величины коэффициентов вязкости и самодиффузии, полученные для упорядоченных структур (уп, Dуп), а также средние значения для упорядоченных и аморфных структур, вычисленные в других компьютерных экспериментах, приведены в таблице 2.2. Все определения дают " жидкостные" значения кинетических свойств: вязкость  ~ (10⁰-10^-2) Пз ( у воды  ~ 10^-2Пз ) коэффициенты самодиффузии - (10^-4 - 10^-5) см2/с. Реальные вещества около абсолютного нуля приобретают свойства хрупкого твердого тела, разрушающегося практически без деформации независимо от того, является ли их структура упорядоченной или разупорядоченной, кристаллической или же аморфной. Их коэффициенты вязкости и диффузии здесь выходят за пределы возможностей измерения; вязкость  превышает 10²⁰ Пз, а коэффициенты самодиффузии становятся меньше 10^-16 см²/с.

Так как течение идёт при Т  0, то оно является "абсолютно безактивационным"; изображающая точка может двигаться лишь в сторону уменьшения энергии, невозможно преодоление даже малых энергетических барьеров. Эксперименты этого раздела надёжно подтверждают безактивационный характер перемещений частиц при релаксации напряжений и при вязком течении в традиционной модели.