1.3 Линейное программирование

1.3.1 Графический метод решения задач линейного программирования

Задача линейного программирования в общей постановке состоит в отыскании значений 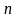переменных 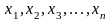, доставляющих экстремумы функции 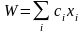при условиях:

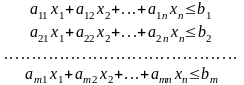
Как следует из приведённых выше приложений, условия представляют собой систему нестрогих линейных неравенств, а показатель эффективности 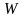является аддитивной линейной функцией переменных.

Для решения задач линейного программирования в зависимости от их специфики применяют различные методы: графический, симплекс-метод, распределительный и др.

Графический метод решения задач ЛП имеет весьма ограниченное применение и главным образом используется для иллюстрации существа подобных задач. В этой связи отметим, что если система ограничений задачи задана в виде системы с двумя переменными, то такая задача может быть решена графически. Если число переменных выше двух, то следует использовать другие методы для решения такой задачи.

На следующем примере продемонстрируем графический метод решения задач линейного программирования. Допустим, что некая фирма выпускает два вида видеокарт. Для производства последних фирма использует ряд компонентов, имеющихся у них на складе в ограниченном количестве. Расход и наименование компонент представлены в табл. 1.1.

Цена видеокарты I 50$, а видеокарты II 60$. Сколько видеокарт каждого вида необходимо произвести для получения максимальной прибыли?

Таблица 1.1

Ресурсы	Запас	Расход ресурсов для производства
		видеокарты I	видеокарты II
Блок памяти	31	3	6
Микрочип JQ31	47	6	8
Транзистор F1	72	10	7

Математическая постановка задачи. Найти 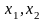, доставляющих максимум целевой функции 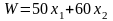, при ограничениях:

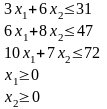
Графическое решение. В системе координат 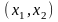строим графики приведённой выше линейной зависимости. Каждый график рассечет плоскость на две полуплоскости. Определяем, какая из полученных полуплоскостей удовлетворяет неравенству. Для этого берём любую точку и её значения подставляем в неравенства. Если неравенство выполняется, значит, найдена нужная полуплоскость, иначе нужная полуплоскость будет противоположной. На рис. 1.4а все полуплоскости, удовлетворяющие неравенству, нарисованы серым фоном, а неудовлетворяющие обозначены штриховой насечкой.

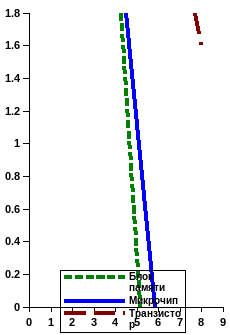
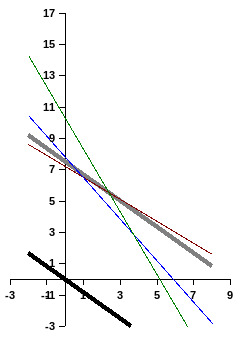
а) б)

Рисунок 1.4 – Графическое решение

Графики неравенств, в совокупности, рассекая плоскость на отдельные участки, формируют многоугольную фигуру, точки внутри которой удовлетворяют всем неравенствам одновременно. Вершины фигуры обведены окружностями.

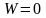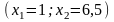Далее на этом же рисунке изображаем прямую, полученную с использованием целевой функции для случая . График данной функции перемещаем параллельно себе до максимально удалённой от неё вершины рис. 1.4б. Из рисунка видно, что данной вершиной является точка пересечения графиков неравенств затрат «транзисторов» и «микрочипов». Эта точка и показывает значения для оптимального производства. Учитывая условия целостности, ответом к задаче будет план производства одной видеокарты первого вида и шести видеокарт второго, а прибыль составит 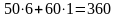ден.ед.