Методы расчета резисторных схем постоянного тока

1.1. Шаговый (рекуррентный) метод

 Этот метод удобно применять в том случае, когда схема представляет собой большое число повторяющихся структурных элементов. Шаговый метод основан на том, что результат первого действия (шага) используется во втором, второй − в третьем и т.д., т.е. число шагов зависит от числа повторяющихся структурных элементов. Задачи подобного типа встречаются довольно часто.

 Задача 1. Найти сопротивление цепи, изображенной на рисунке.

 Решение.

 Перечертим схему в более удобном для расчетов и наглядном виде (рис.).

 Теперь очевидно, что цепь представляет собой несколько «вложенных» друг в друга групп резисторов, соединенных параллельно.  Начнем пошаговое вычисление эквивалентных сопротивлений, начиная с самых «внутренних» элементов. Заменив резисторы R₄, R₅, R₆ резистором

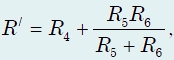
получим новую схему (рис.).

 Поступая аналогично с резисторами R₂, R₃ и R^/, получим в результате простую схему (рис.),

где R^// определяется выражением:

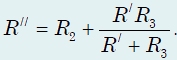
 Эквивалентное сопротивление всей цепи равно

 Решение задач подобного типа значительно облегчается, если некоторые группы резисторов имеют одинаковые значения сопротивлений. Рассмотрим, например, следующую задачу.

 Задача 2. Найти сопротивление цепи АВ, изображенной на рисунке.

 Решение.  Рассчитывать эквивалентное сопротивление начнем слева. Два параллельно соединенных резистора, сопротивления которых одинаковы и равны 2R каждый, можно заменить резистором эквивалентным сопротивлением R. Этот резистор соединен последовательно с резистором того же сопротивления R. Заменим и эти два резистора одним, имеющим эквивалентное сопротивление 2R. Опять получим два резистора одинакового сопротивления 2R, соединенных параллельно. И их можно заменить резистором эквивалентным сопротивлением R и т.д. В результате получим, что эквивалентное сопротивление всей цепи АВ равно R.

1.2. Метод преобразования

 Хотя этот метод не дает конкретного алгоритма решения задач, но облегчает подход к нему. Преобразования основаны на простом принципе: точки равного потенциала можно соединять в один узел. Рассмотрим классический пример.

 Задача 1. Найти сопротивление цепи АВ, изображенной на рисунке.

 Решение.

 Так как сопротивления подводящих проводов равны нулю, то точки АА^/ и ВВ^/ попарно равнопотенциальны. Соединяя эти точки, получим простую схему из трех параллельных резисторов (рис.),

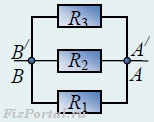
сопротивление которой

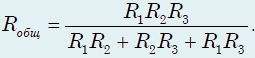
 Рассмотрим более сложную задачу того же типа.

 Задача 2. Найти сопротивление цепи, изображенной на рисунке, если сопротивления всех резисторов одинаковы и равны R.

 Решение.  Пронумеруем все узловые точки этой цепи − их всего шесть. Потенциалы точек 1 и 3 одинаковы, поэтому объединим эти точки в одну. То же самое сделаем с парами точек 2 и 5, 4 и 6. Получившаяся в результате цепь дана на рис.

 Ее эквивалентное сопротивление равно R/2.

1.3. Метод равнопотенциальных узлов

 Здесь рассмотрены задачи, решение которых сопровождается последовательным преобразованием исходной схемы. Причем наибольшее изменение схема обычно претерпевает после первого эвристического шага, связанного с использованием метода равнопотенциальных точек (узлов). Дальнейшие преобразования связаны с эквивалентной заменой последовательных или параллельных резисторов. Такие задачи представляют определенный учебный интерес для развития творческих способностей учащихся, они довольно часто встречаются в различных учебных пособиях. Обычно это симметричные цепи, составленные из одинаковых элементов без обозначенных резисторов.  Для преобразования цепи и дальнейшего расчета ее сопротивления воспользуемся тем свойством, что во всякой цепи точки с одинаковыми потенциалами можно соединять в узлы. И обратно: узлы цепи можно разделять, если после разделения потенциалы точек, входивших в узел, не изменятся. Подчеркнем, что в каждом конкретном случае обязательна проверка равенства потенциалов получившихся точек. Упрощение подобного рода возможно потому, что ток между этими точками не идет, и между ними можно включать любые резисторы. Рассмотрим простейшую задачу.

 Задача 1. На участке АВ схемы с однородными по всей длине проволочными резисторами укажите точки с равными потенциалами (рис.).

 Решение.  Предположим, потенциал точки А равен 10 В, а потенциал точки В равен нулю − точка В заземлена. От точки А до точки В потенциал равномерно и непрерывно уменьшается от 10 В до нуля, т.к. проволоки однородны.  Предположим, что в некоторой точке М потенциал равен 5 В. Тогда на прямой АВ обязательно найдется точка М^/, потенциал которой также равен 5 В.  Аналогично и для точек К и К^/, потенциалы которых равны (в данном случае 7,5 В). Таких точек с равными потенциалами можно указать бесчисленное множество. Если теперь точки М и М^/ соединить любым резистором, в том числе нулевого сопротивления, т.е. просто совместить (рис.),

сопротивление цепи не изменится. Справедливо и обратное − узел ММ^/ можно раз делить на два узла: М и М^/.