ГОУ ВПО

ДВГУПС

Кафедра “Физика”

Лабораторная работа _{На тему: “Проводники в электрическом поле”.}

1Э 115

Номер работы Группа

Выполнил:

Строкаченко Н.Ю

Проверил:

Хабаровск 2007 г.

ТЕМА: ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Цель работы:

1. Определить электроемкость конденсаторов.

2. Экспериментально проверить формулы для параллельного и после­довательного соединения конденсаторов.

3. Определить энергию заряженных конденсаторов.

Приборы и принадлежности: гальванометр; источник тока; панель с вольтметром и переключателями; конденсаторы.

1. Теоретическая часть

1. Распределение заряда в заряженном проводнике

Все тела в зависимости от их электрических свойств можно разделить на три группы: проводники, диэлектрики, полупроводники. В незаряженном металлическом проводнике, как и в любом нейтральном теле, суммарный электрический заряд равен нулю, т.е. заряд свободных электронов ком­пенсируется положительными зарядами, связанными с узлами крис­таллической решетки металла. Так как заряд тел определяется недостат­ком или' избытком числа электронов по сравнению с числом их в электри­чески нейтральных телах, то заряжение проводника, т.е. его электризация, сводится к изменению, тем или иным способом, числа содержащихся в нем электронов.

Каким же образом распределяется в проводнике этот избыточный заряд?

Неподвижные заряды одного и того же знака не могут сохраниться в толще заряженного проводника. Силы взаимного отталкивания заставят их удалиться друг от друга на наибольшие расстояния, пока не будет достиг­нута граница проводника с диэлектриком, т.е. на внешнюю поверхность проводника.

Для того, чтобы распределение заряда на проводнике было равновес­ным, вектор электрической индукции (электрического смещения) внутри проводника должен быть равен нулю (в противном случае заряды внутри проводника будут перемещаться и равновесие нарушится):

Тогда и поток вектора индукции через любую замкнутую поверхность расположенную внутри проводника, равен нулю. Следовательно, алгеб­раическая сумма зарядов, охватываемых любой замкнутой поверхностью внутри проводника, также равна нулю, т. е.

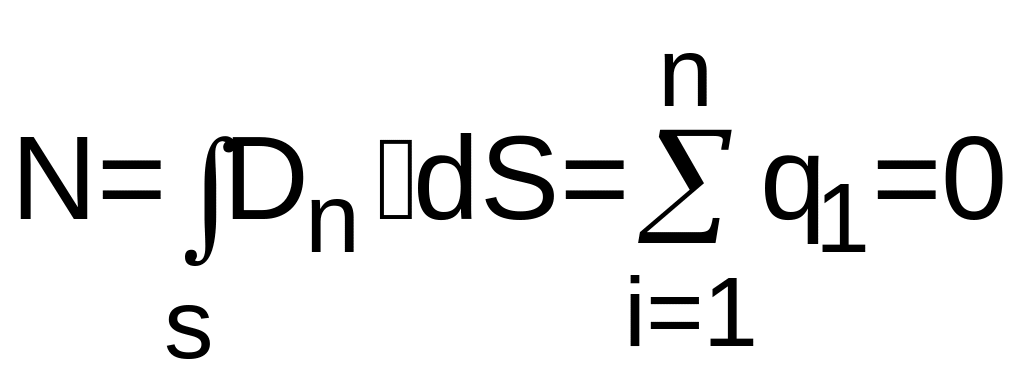
Таким образом, внутри проводника суммарный электрический заряд равен нулю. Сообщенный проводнику заряд распределяется только по внешней поверхности проводника.

Количественной характеристикой распределения заряда по поверхно­сти проводника является поверхностная плотность заряда

где S - поверхность проводника, на которой распределен заряд q.

Тело произвольной формы на различных участках поверхности имеет разную плотность заряда. Распределение поверхностной плотности заря­да определяется только формой проводника и не зависит от величины за­ряда. Чем значительнее кривизна выпуклой поверхности заряженного те­ла, тем больше поверхностная плотность заряда.

Вблизи заряженного проводника вектор электрической индукции чис­ленно равен поверхностной плотности заряда, а напряженность прямо пропорциональна поверхностной плотности заряда.

где и - нормальные составляющие вектора электрической индукции и напряженности поля.

1.2. Потенциал заряженного проводника

Т ак как в статистически заряженном проводнике напряженность поля внутри проводника равна нулю, то, используя связь между напряженно­стью и разностью потенциалов электрического поля

можно сделать вывод, что при Е = О

Следовательно, весь объем проводника является эквипотенциальным: потенциал во всех точках проводника, включая и точки его поверхности, постоянен.

Если удалить проводник из электрического поля, наведенные заряды исчезают, части проводника снова становятся незаряженными.