- •1. Теоретическая основа лабораторной работы
- •1.1.1 Апериодическое тз.
- •2 Основные сведения о програме matlab и приложении simulink
- •2.1 Общие сведения
- •2.2 Запуск Simulink
- •2.3 Обозреватель разделов библиотеки Simulink
- •2.4 Создание модели
- •2.5 Окно модели
- •3 Порядок выполнения лабораторной работы
- •4 Отчет о проделанной работе
- •Контрольные вопросы
- •Список использованных источников
- •Приложение 1
Министерство образования и науки
Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ
УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА
(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)»
(СГАУ)
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ТИПОВЫХ ЗВЕНЬЕВ В ПРОГРАММНОМ ПАКЕТЕ
MATLAB SIMULINK
Методические указания
к лабораторным работам
Самара 2013
УДК 681.5.011
ББК
Составители: Гимадиев А.Г., Крючков А.Н., Быстров Н.Д., Ермилов М.А.
Исследование характеристик типовых звеньев в программном пакете Matlab Simulink [Электронный ресурс] : электрон. метод. указания
Изложены методические основы моделирования систем управления с использованием пакета программ Matlab Simulink. Детально проработаны вопроса набора моделей элементов САУ-типовых звеньев и построение их динамических характеристик.
Методические указания рекомендуются для студентов, обучающихся по специальностям 150802 ‑ "Гидравлические машины, гидроприводы и гидропневмоавтоматика; 160301 ‑ " Авиационные двигатели и энергетические установки", а также по направлениям бакалавриата 151000 ‑ "Технологические машины и оборудование"; 141100 "Энергетическое машиностроение" и могут быть полезны при выполнении курсовых работ, дипломных проектов и подготовке к экзаменам. Подготовлено на кафедре АСЭУ.
-
© Самарский государственный
аэрокосмический университет, 2013
1. Теоретическая основа лабораторной работы
Любую систему автоматического регулирования (САР) можно представить в виде соединения отдельных типовых звеньев. Типовым звеном (ТЗ) называют элемент или узел системы регулирования, который независимо от физической природы процессов, протекающих в нем, одинаково реагирует на один и тот же вид возмущения. Это означает, что два или несколько звеньев САР будут одного типа, если они имеют одинаковую функциональную зависимость между входным и выходным параметрами.
Для всех ТЗ характерны некоторые общие признаки: каждое ТЗ имеет четко обозначенный вход и выход; сигнал через ТЗ распространяется в одном направлении - со входа на выход. В структурных схемах САР типовое звено обозначают в виде прямоугольника, внутри которого записывается его функциональная зависимость, выраженная в операторной форме (передаточная функция).
Разбивка САР на ТЗ облегчает анализ и синтез систем, так как позволяет воспользоваться хорошо разработанными в теории автоматического регулирования (ТАР) методами.
По виду функциональной зависимости ТЗ подразделяются на апериодическое, колебательное, дифференцирующее, интегрирующее, усилительное и звено чистого запаздывания. Это основные типы звеньев, с использованием которых могут быть получены другие типовые звенья, но не более второго порядка (по виду дифференциального уравнения). Управление ТЗ систем регулирования выводятся на основе тех или иных физических законов, по которым протекают процессы в звеньях. При исследовании динамики в САР нужно уметь не только выделять ТЗ в системе регулирования и составлять их уравнения, но и определять численные значения входящих в уравнения коэффициентов. Существует два метода определения этих коэффициентов: расчетный и экспериментальный. Расчетный метод не во всех случаях достаточно точен. Принятые при выходе уравнения допущения могут привести к существенным ошибкам. Поэтому на этапе доводки САР часто применяют экспериментальный метод определения коэффициентов. При этом можно воспользоваться переходными или частотными характеристиками ТЗ.
В качестве примеров рассмотрены звенья, которые часто реализуются в САР авиационных двигателей. При выводе уравнений ТЗ основная трудность заключается в обосновании и принятии упрощающих допущений. Учет многих факторов приводит к усложнению расчетной модели, а принятие грубых допущений - к исключению из анализа основных свойств звена. Поэтому нужно всегда иметь в виду, в рамках какой расчетной динамической модели системы будет исследоваться то или иное звено.
1.1 Переходные характеристики
Переходная
характеристика ТЗ представляет собой
изменение во времени выходного параметра
звена
![]() при ступенчатом входном сигнале
при ступенчатом входном сигнале
![]() (1)
(1)
и нулевых начальных условиях.
В формуле (1) приняты
обозначения:
![]() - величина ступени входного сигнала;
- величина ступени входного сигнала;
е![]() диничная
ступенчатая функция
диничная
ступенчатая функция
(функция Хевисайда).
Переходная характеристика или переходная функция определяется как решение дифференциального уравнения ТЗ при ступенчатом входном сигнале.
1.1.1 Апериодическое тз.
![]() (2)
(2)
Переходная функция
этого ТЗ определяется как решение
дифференциального уравнения (2). Известно,
что решение неоднородного дифференциального
уравнения (2) складывается из общего
решения
![]() однородного уравнения
однородного уравнения
![]() (3)
(3)
и частного решения
![]() неоднородного уравнения (2)
неоднородного уравнения (2)
![]() (4)
(4)
Переходная функция апериодического ТЗ:
![]() (5)
(5)
График переходной
функции апериодического ТЗ (рисунок
1.1,а) представляет экспоненциальную
нарастающую кривую. Значения
![]() при
при
![]() и
и
![]() определяются, соответственно, выражениями:
определяются, соответственно, выражениями:
![]()
|
а) |
|
б) |
|
в) |
Рисунок 1.1 - Переходные характеристики апериодического типового звена |
Следовательно,
постоянная времени
![]() равна времени, в течение которого
выходной параметр достигает величины
0,632 от нового установившегося значения.
Чем больше постоянная времени
,
тем медленнее протекает переходной
процесс в ТЗ (рисунок 1.1,б). Обычно
переходной процесс считается законченным,
если
равна времени, в течение которого
выходной параметр достигает величины
0,632 от нового установившегося значения.
Чем больше постоянная времени
,
тем медленнее протекает переходной
процесс в ТЗ (рисунок 1.1,б). Обычно
переходной процесс считается законченным,
если
![]() достиг 95% своего установившегося
значения, т. е.
достиг 95% своего установившегося
значения, т. е.
![]() .
Это соответствует времени
.
Это соответствует времени
![]() ,
т. е. переходной процесс апериодическом
ТЗ можно считать практически законченным
по истечении времени
,
т. е. переходной процесс апериодическом
ТЗ можно считать практически законченным
по истечении времени
![]() .
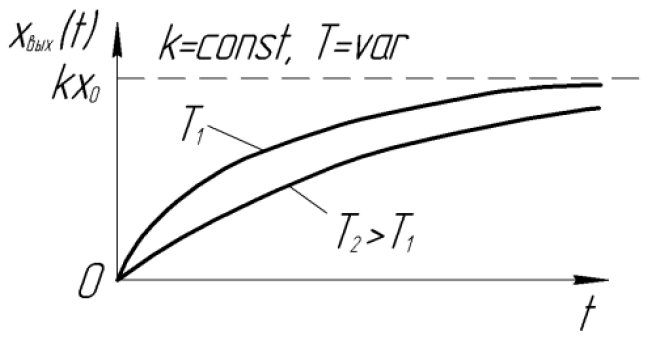
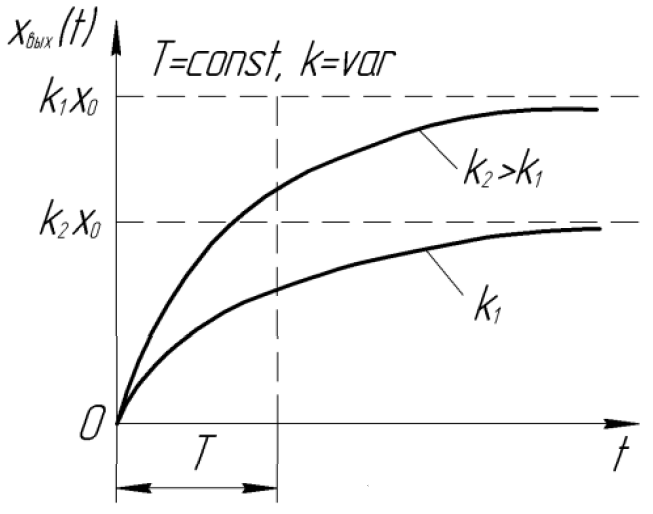
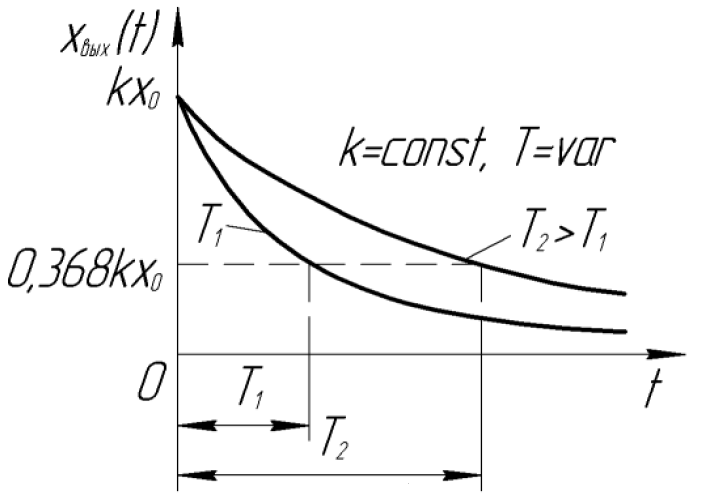
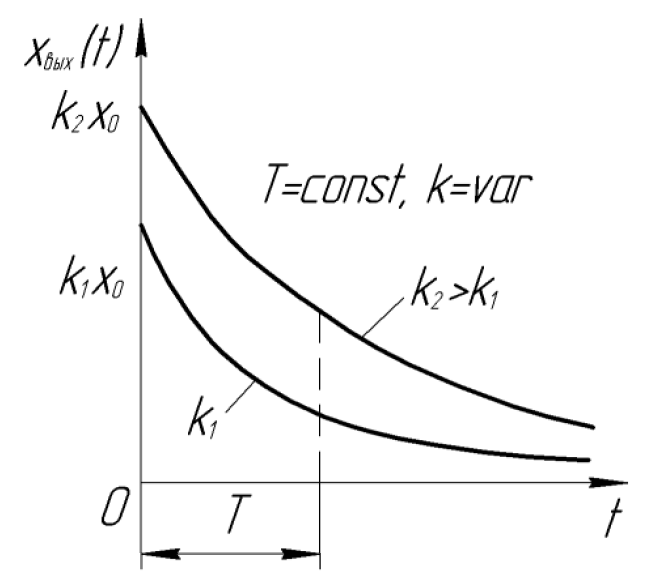
При различных значениях коэффициента
передачи
.
При различных значениях коэффициента
передачи
![]() ,
но одинаковом
переходные характеристики отличаются
лишь величиной выходного параметра, а
время переходного параметра, а время
переходного процесса
,
но одинаковом
переходные характеристики отличаются
лишь величиной выходного параметра, а
время переходного параметра, а время
переходного процесса
![]() этих звеньев одинаковое (рисунок 1.1,в).
этих звеньев одинаковое (рисунок 1.1,в).
1.1.2 Колебательное ТЗ
Из теоретической механики известно, что любую колебательную систему с одной степенью свободы можно описать дифференциальным уравнением второго порядка
![]() (6)
(6)
где
![]() - постоянная времени, характеризующая
собственную частоту колебаний системы;
- постоянная времени, характеризующая
собственную частоту колебаний системы;
![]() - коэффициент
демпфирования;
- коэффициент
демпфирования;
![]() - коэффициент
усиления, или коэффициент передачи.
- коэффициент
усиления, или коэффициент передачи.
После решения
дифференциального уравнения (6) при
![]() получим переходную функцию колебательного
ТЗ
получим переходную функцию колебательного
ТЗ
![]() (7)
(7)
где
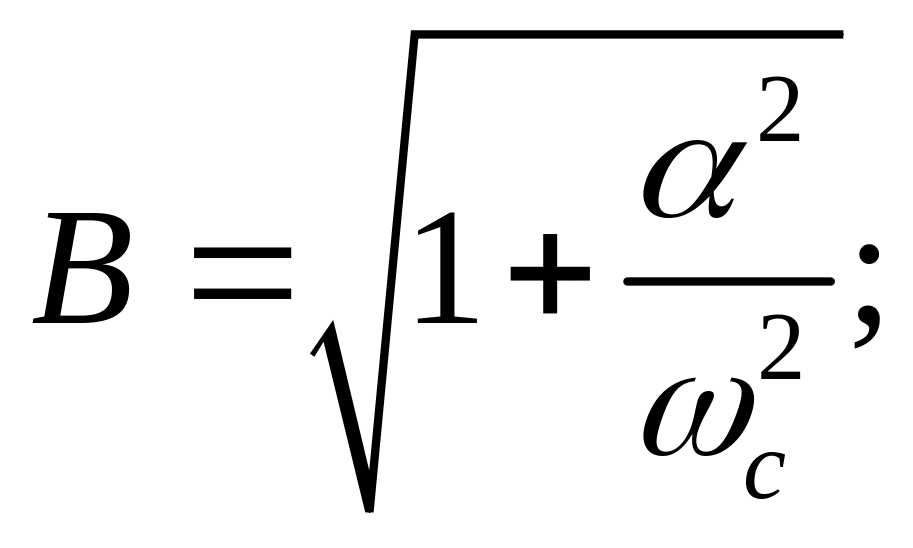
![]()
![]() - коэффициент,
характеризующий затухание колебаний
в ТЗ;
- коэффициент,
характеризующий затухание колебаний
в ТЗ;
![]() - собственная
частота колебаний ТЗ;
- собственная
частота колебаний ТЗ;
![]()
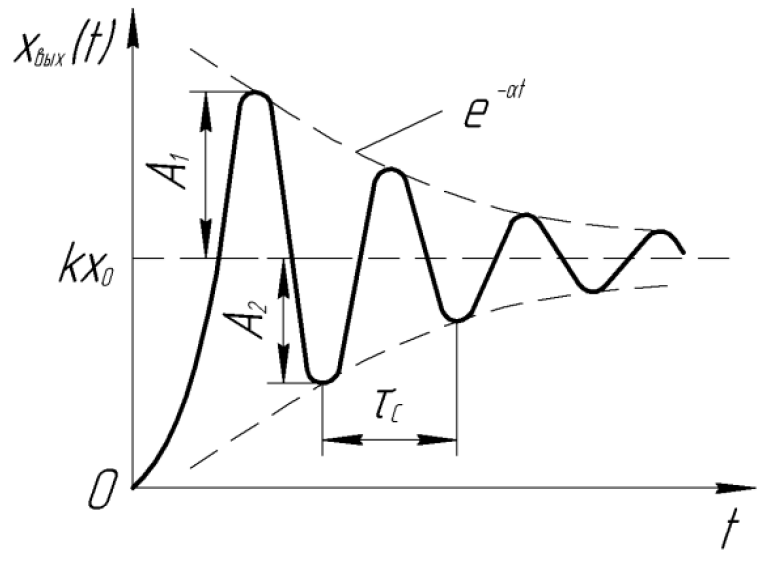
Из анализа переходной
характеристики (рисунок 1.2,а), построенной
по формуле (7), следует, что при коэффициенте
демпфирования
переходной процесс в колебательном ТЗ
сопровождается затухающими колебаниями
с частотой
![]() и амплитудой, уменьшающейся по экспоненте
и амплитудой, уменьшающейся по экспоненте
![]() .
.
|
а) |
|
б) |
|
в) |
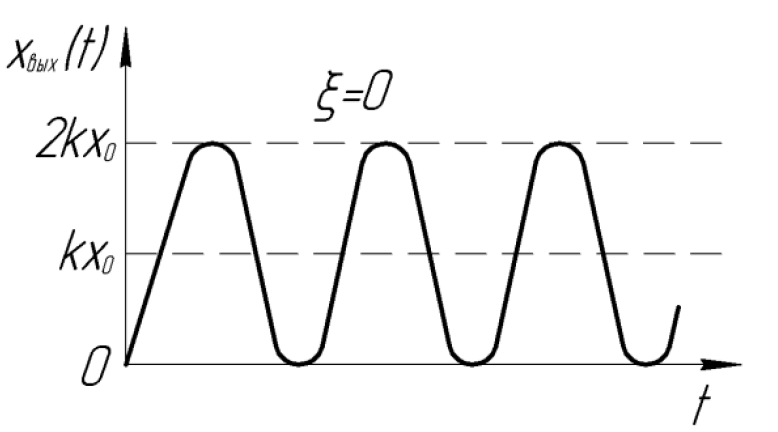
Рисунок 1.2 - Переходные характеристики колебательного типового звена
При
1.1.3 Реальное дифференцирующее ТЗ Дифференцирующее типовое звено может быть идеальным и реальным. Реальное дифференцирующее ТЗ описывается зависимостью
где k - коэффициент передачи звена; T - постоянная времени.
Переходная
функция реального дифференцирующего
ТЗ определяется из решения
дифференциального уравнения (8) при
Переходная
характеристика (рисунок 1.3,а) реального
дифференцирующего ТЗ по формуле (9),
представляет нисходящую экспоненциальную
кривую. При
а)
б)
в) Рисунок 1.3 ‑ Переходные характеристики реального дифференцирующего типового звена
1.2 Частотные характеристики Частотные характеристики ТЗ получают при гармоническом входном воздействии, заданном либо в тригонометрической форме
либо в экспоненциальной форме
При этом выходной
сигнал изменяется также по гармоническому
закону (рисунок 1.4) с той же частотой
,
но с другой амплитудой
или
Рисунок 1.4 – График выходного сигнала типового звена при подаче на вход гармонического сигнала
Зависимость
отношения комплексной амплитуды
где
Частотная характеристика ТЗ может быть представлена на комплексной плоскости, если предварительно представить частотную функцию в виде
где
Частотная
характеристика ТЗ на комплексной
плоскости называется амплитудно-фазо-частотной
характеристикой (АФЧХ) типового звена.
Частотная функция ТЗ может быть
получена из выражения для его
передаточной функции
где
1.2.1 Апериодическое ТЗ Дифференциальное уравнение (2) этого звена, записанное в операторной форме, имеет вид
Решив его
относительно
Заменив в
соотношении (10)
Тогда АЧХ и ФЧХ будут определяться из выражений
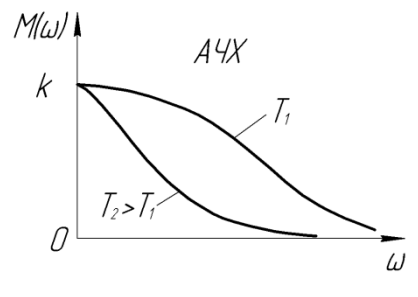
Из формулы (12)
для АЧХ апериодического ТЗ следует,
что с увеличением частоты колебаний
величина
а)
б)
в) Рисунок 1.5 – Частотные характеристики апериодического звена 1.2.2 Колебательное ТЗ Дифференциальное уравнение (6) колебательного ТЗ, записанное в операторной форме, имеет вид
Передаточная и частотные функции определяются соотношениями
а)
б)
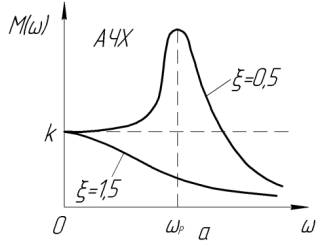
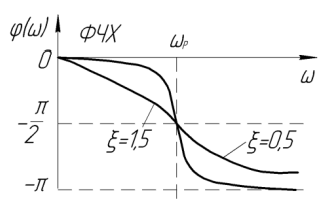
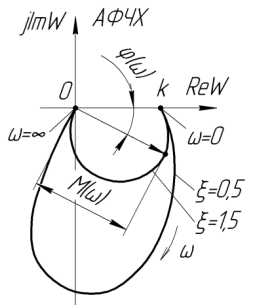
в) Рисунок 1.6 – Частотные характеристики колебательного ТЗ Модуль и аргумент частотной функции, полученные из выражения (14), имеют вид
При значениях
коэффициента демпфирования
При
1.2.3 Реальное дифференцирующее ТЗ Операторное уравнение реального дифференцирующего ТЗ в соответствии с формулой (8) имеет вид
Передаточная и частотная функции определяются равенствами
АЧХ и ФЧХ, определенные из соотношения (38), имеют вид
АЧХ реального
дифференцирующего звена (рисунок
1.7,а) имеет вид нарастающей кривой,
что указывает на то, что это звено
обладает свойством фильтра высоких
частот: хорошо пропускает колебания
высоких частот и плохо — колебания
низких частот. Сдвиг по фазе (
а)
б)
в) Рисунок 1.7 – Частотные характеристики дифференцирующего ТЗ
|





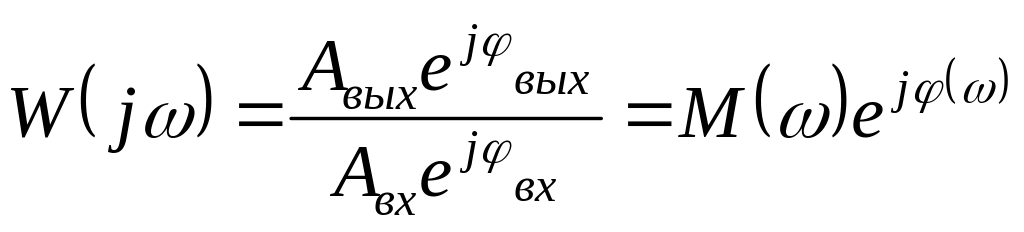 ,
,