4. Проведение эксперимента по снятию переходных функций

На объекте устанавливается рабочий режим и производится измерение всех параметров технологического объекта. В момент времени, когда наносится выбранный вид и амплитуда испытательного воздействия и производится непрерывное измерение , которая через некоторый момент времени 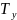будет иметь установившуюся величину.

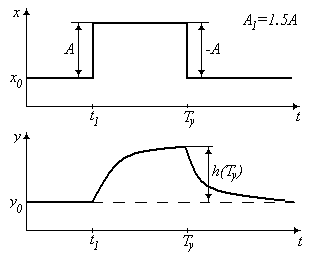
Рис. 7 Реакция объекта на испытательное воздействие

Линейность статической характеристики не означает линейность динамической характеристики в малом. Для подтверждения линейности динамической характеристики в малом необходимо убедиться в соблюдении принципа суперпозиции для чего опыт проводят при различных знаках и величинах . Далее вычисляют коэффициент усиления 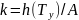. Если отличается от 20 до 40%, то необходимо уменьшить и провести повторное снятие функции. В некоторых случаях гладкие переходные функции при одном и том же режиме и при одних и тех же фиксированных моментах времени в одних и тех же опытах имеют различные значения. Для проверки стационарности динамических характеристик необходимо эксперимент по снятию функции повторить несколько раз через определенные промежутки времени. Опыты необходимо проводить при одних и тех же и .

5. Обработка результатов эксперимента по снятию переходных функций

1. Обработка гладких переходных функций.

Полученные переходные функции строятся в одном масштабе, но так как величина в опытах изменялась, то переходные функции необходимо представить в виде единичных переходных функций (ЕПФ):

Которые строятся в одном масштабе. Если разброс между ЕПФ 1÷2%, то для последующей обработки выбирается одна из ЕПФ. Если разброс больше 2÷3%, то выбирают усредненную ЕПФ:

По данным ЕПФ определяется время запаздывания (𝜏) — отрезок времени для которого выполняется следующее неравенство , где ∆ — значение ЕПФ равное ∆=(0,01÷0,02) .

Рис. 8 График ЕПФ

∆ — определяется классом точности выбранных приборов.

2. Сглаживание экспериментальных переходных функций.

Во многих случаях функции получаются гладкими. То есть получается зависимость вида:

где — помеха (нормальное распределение величины с ).

генерируется либо в самом объекте, либо наводится в измерительной цепи.

Рис. 8 График случайного процесса

Цель обработки 2.5.12 получение истинных значений в гладкой форме по которой можно выделить динамические свойства объекта. Для этого необходимо снять экспериментальных переходных функций с тем, чтобы

С данной зависимости 2.5.13 необходимо снять от 80÷100 . В промышленности данный метод не используется, а используется “сглаживание” переходной функции 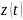основанное на усреднении заданных таблично отстоящих друг от друга на (таких ординат берется ). При этом предполагается, что переходная функция носит неколебательный характер, то есть корни ХАУ вещественные и меньше ноля.

1. Сглаживание переходных функций скользящим усреднением.

Сущность метода заключается в последовательном усреднении ординат переходной функции на некотором интервале , где — цело, чётное число.

Алгоритм согласования имеет следующий вид:

где — оценка ординаты отнесенная к середине интервала сглаживания;

— предыдущее значение величины;

— память у линейного фильтра, АФХ которого имеет вид:

то есть данный фильтр не пропускает частоты выше откуда находят .

Увеличение величины может привести к искажению переходной функции и потере части уже сглаженных координат (особенно в начале) при:

Так как спектр частот обычно не известен, а также не известна спектральная плотность помехи , то величину находят экспериментально. При этом, чтобы получить значение всех координат измерение 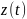начинается до момента нанесения активного воздействия , а также после завершения процесса. Начальный участок определяет начальную структуру, который будет аппроксимировать данную переходную функцию, а последний участок определяет коэффициент усиления модели.

2. Сглаживание методом четвертых разностей.

Сущность метода заключается в аппроксимации с помощью метода наименьших квадратов каждых пяти соседних ординат параболой второго порядка, затем вычисляется разность между средним значением из данных пяти ординат и параболой второго порядка. Величина данной поправки равна центральной четвертой разности функции :

Далее находим значение функции:

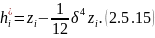
В данном случае мы теряем четыре ординаты:

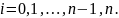
Для того чтобы восполнить эти потери применяются следующие формулы:

Кроме рассмотренных методов сглаживания применяется сглаживание рядами Фурье и полиномами Чебышева, но они очень сложные.

Усреднение переходных функций методами четвертых разностей дает лучшие результаты, потому что этот метод основан на определении, что на интервале усреднения переходная функция имеет вид параболы.