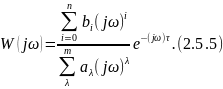- •«Моделирование объектов и систем управления отрасли»
- •Введение
- •Методы моделирования объектов и систем управления
- •Физическое моделирование объектов и систем управления
- •Метод подобия
- •Метод аналогий
- •Математическое моделирование химико-технологических процессов
- •Сущность, свойства и этапы математического моделирования химико-технологического процесса
- •Основные виды математических моделей химико-технологических процессов
- •Блочный принцип разработки математических моделей химико-технологических процессов
- •Основные подходы получения математических моделей химико-технологических процессов
- •Классификация экспериментальных методов. Виды математических моделей.
- •Модели динамики (статистические) химико-технологического процесса
- •Определение динамических характеристик химико-технологических процессов при активном эксперименте
- •Проведение эксперимента по снятию переходных функций
- •Обработка результатов эксперимента по снятию переходных функций
- •Получение динамических характеристик объекта по переходным функциям
- •Определение динамических характеристик объектов при входных воздействиях в виде случайных сигналов
- •Свойства и характеристики стационарных случайных процессов
- •Постановка эксперимента по определению статистических характеристик процессов
- •Определение динамических характеристик объектов и систем управления методом моментов
- •Применение метода модулирующих функций для определения динамических характеристик объектов и су
- •Получение модели статики объектов и су
- •Определение моделей статики (уравнения регрессии) при пассивном эксперименте
- •Регрессионный анализ в матричной форме
- •Получение модели статики при активном эксперименте
- •Детерминированные (аналитические) модели химико-технологических процессов
- •Использование уравнений материального и теплового баланса для описания стационарных и нестационарных режимов протекания химико-технологических процессов
- •Модели структуры потоков, как основа построения математических моделей гидромеханики химико-технологического процесса
- •Модель идеального перемешивания
- •Модель идеального вытеснения
- •Диффузионные модели
- •Однопараметрическая диффузионная модель (одм)
- •Двухпараметрическая диффузионная модель
- •Ячеечная модель
- •Математическое описание тепловых процессов
- •Прямоточные кожухотрубчатые теплообменники
- •Противоточный кожухотрубчатый теплообменник
- •Математические модели теплообменников с учетом накопления тепла в стенке
- •Прямоточный кожухотрубчатый теплообменник
- •Противоточный кожухотрубчатый теплообменник
- •Математическая модель конденсатора (паровой теплообменник)
- •Передаточные функции теплообменных аппаратов
- •4.5.1 Конденсатор без учета накопления тепла в станке
- •4.5.2 Конденсатор с учётом накопления тепла в стенке
- •4.5.3 Кожухотрубчатый противоточный теплообменник
- •Математическое моделирование массообменных аппаратов
- •Математическая модель процесса газоабсорбции
- •Математическая модель процесса ректификации
- •Передаточная функция ректификационной колонны
- •Математическое моделирование математических процессов
- •Математическая модель процесса химического превращения (кинетическая модель)
- •Математическая модель химического реактора идеального перемешивания
- •Математическая модель реактора идеального вытеснения
- •Передаточные функции химических реакторов
- •Передаточная функция реактора идеального перемешивания простого типа
- •Реактор идеального вытеснения
- •Математическое моделирование динамики типовых контуров регулирования технологических параметров объекта
- •Свойства, характеристики и классификация объектов регулирования
- •Регулирование уровня в резервуарах
- •Регулирование расхода жидких сред
- •Регулирование расхода сыпучего материала
- •Регулирование концентрации вещества в смесителях. Регулирование концентрации вещества в смесителях
- •Регулирование температуры в смесителях идеального перемешивания
- •Регулирование состава смеси в реакторе с мешалкой
- •Методы и алгоритмы идентификации динамических систем
- •Общая классификация задач идентификации
- •Постановка задачи идентификации
- •Идентификация непрерывных объектов в классе моделей с дискретным временем
- •Задача непараметрической идентификации
- •Задачи параметрической идентификации
- •Безпоисковые алгоритмы идентификации с адаптивной моделью (баиам)
- •8.6.1 Общая структура баиам в пространстве сигналов
- •8.6.2. Общая структура баиам с дискретным временем и операторным описанием
- •Оптимизация химико-технологических с использованием математических моделей
- •Постановка задач оптимизации
- •Поисковые модели идентификации с адаптивной моделью (пмиам)
- •Аналитические методы оптимизации
- •Метод классического анализа функций
- •Метод неопределенных множителей Лагранжа
- •Линейное программирование
- •Нелинейное программирование
- •Численные методы оптимизации. Постановка задачи оптимизации
- •Реализация методов оптимизации в пакете MatLab (toolbox)
- •Оптимизация (минимизация) функции
- •9.5.5. Использование метода наименьших квадратов для решения задач оптимизации
Классификация экспериментальных методов. Виды математических моделей.
Основным источником информации является эксперимент. Все экспериментальные методы делятся на следующие виды:
экспериментально-статистические методы


пассивный эксперимент
модель статики
модель динамики
активный эксперимент
модель статики
модель динамики
Рис. 5 Схема, отображающая основные виды экспериментов и их составляющие
Каждому сочетанию вида эксперимента и вида получаемой модели соответствуют определенные статистические методы: методы корреляционного и регрессивного анализов, методы, основанные на теории правдоподобия и др.. Для получения модели динамики при пассивном эксперименте применяются методы теории случайных чисел (метод моментов и др.). Для получения математической модели в статике при активном эксперименте применяются методы ортогонального планирования, симплекс планирование и др..
Модель динамики при активном эксперименте получается при помощи метода случайных функций с учетом вида взаимодействия (метод последовательного логарифмирования и др.).
Наиболее эффективным и удобным представлением модели статики является представление её в виде полинома вида:
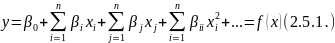
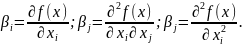
где
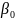 ,
,
 ,
,
 ,
,
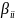 — теоретические коэффициенты полинома.
— теоретические коэффициенты полинома.
Данные полинома могут быть получены при бесконечном числе опытов и при отсутствии возмущающих воздействий.
В реальном ХТП всегда присутствует возмущающее воздействие, и количество опытов ограничено и называется выборкой. Поэтому полученная модель является оценкой соответствующего теоретического уравнения 2.5.1. и называется уравнением регрессии следующего вида:
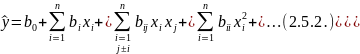
где
 — приближенное значение;
— приближенное значение;
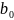 ,
,
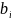 ,
,
 ,
,
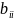 ,
,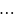 — оценки соответствующих теоретических
коэффициентов и называются коэффициентами
уравнения регрессии;
— оценки соответствующих теоретических
коэффициентов и называются коэффициентами
уравнения регрессии;
— свободный член;
— линейный эффект (линейное влияние на );
— эффект попарного взаимодействия;
— квадратичный эффект.
Данная полиномиальная форма 2.5.2. удобна и эффективна так как:
увеличивается точность математического описания ХТП;
она позволяет сравнительно просто определить коэффициенты уравнения с помощью ЭВМ.
Модели динамики (статистические) химико-технологического процесса
Основные виды возмущающих воздействий и основные виды получаемых моделей.
Для
получения статистической модели динамики
химико-технологического процесса (ХТП)
создается испытательное возмущающее
воздействие
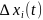 и измеряется изменение
и измеряется изменение
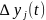 объекта
.
Полученное выражение
является решением с
в правой части с нулевыми начальными
условиями
объекта
.
Полученное выражение
является решением с
в правой части с нулевыми начальными
условиями
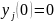 .
То есть подбирается такая аппроксимирующая
функция (то есть решение дифференциального
уравнения), которая совпадает с данной
экспериментальной зависимостью
.
То есть подбирается такая аппроксимирующая
функция (то есть решение дифференциального
уравнения), которая совпадает с данной
экспериментальной зависимостью
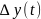 .
Точность получаемой модели зависит от
точности аппроксимации
решение дифференциального уравнения.
.
Точность получаемой модели зависит от
точности аппроксимации
решение дифференциального уравнения.
По виду испытательных возмущений различают пассивный и активный эксперимент. При пассивном в качестве используются случайные функции входной координаты .
Экспериментальный
метод получения модели динамики
базируется на предположении
сосредоточенности переменных, на
линейности статической характеристики
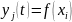 и стационарности процесса. Это позволяет
описать динамику процесса в виде
однородного дифференциального уравнения.
и стационарности процесса. Это позволяет
описать динамику процесса в виде
однородного дифференциального уравнения.
ХТП
являются процессами с распределенными
параметрами. Данные ХТП могут быть
представлены как объекты сосредоточенными
параметрами, распределённость может
быть учтена в модели звеном чистого
запаздывания. При небольшом изменении
входных переменных
 можно принять зависимость линейной.
Все ХТП являются нестационарными, но
на интервале изменения
данный ХТП является стационарным, так
как динамические свойства меняются
медленно.
можно принять зависимость линейной.
Все ХТП являются нестационарными, но
на интервале изменения
данный ХТП является стационарным, так
как динамические свойства меняются
медленно.
Вывод: с учетом всех допущений динамическую модель ХТП можно представить в виде однородного дифференциального уравнения.
Динамическую модель можно представить в виде:
однородными дифференциальными уравнениями
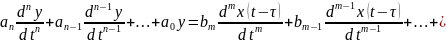
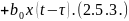
где
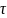 — чистое запаздывание.
— чистое запаздывание.
передаточными функциями

амплитудно-фазовыми характеристиками