8.6.2. Общая структура баиам с дискретным временем и операторным описанием

В данном случае объект описывается оператором 8.6.1. Однако входные и выходные сигналы квантуются во времени. На структурной схеме алгоритма квантования можно изобразить с помощью преобразователя .

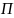Структурная схема БАИАМ с дискретным временем и операторным описанием имеет вид:

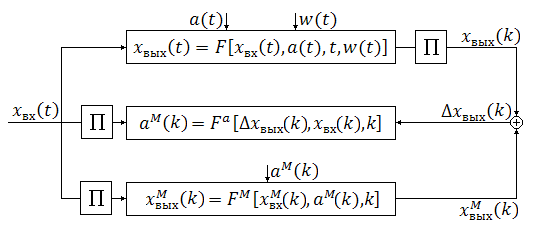
Рис. 47

В качестве может быть использован АЦП (квантователь во времени в случае большой разрядности).

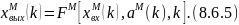
При этом алгоритм настройки, который реализует данный БАИАМ, имеет следующий вид:

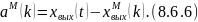
при котором настраиваемая модель имеет операторное описание при операторном описании идентифицируемого объекта (Рис. 48).

Рис. 48

Структура ПАИАМ с дискретным временем и операторным описанием (см. Рис. 47 с учетом части структуры, обведенной пунктирной линией на Рис. 48).

В данных структурах блоки “вычисление целевой функции”, “формирование процесса настойки”, ”алгоритм поиска” не раскрываются, так как они могут быть разными для ПАИМ. Алгоритм настройки должен обеспечивать .

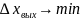9. Оптимизация химико-технологических с использованием математических моделей

1. Постановка задач оптимизации

Оптимизация любого химико-технологического заключатся в нахождении оптимума рассматриваемой функции связанной с математической моделью.

2. Поисковые модели идентификации с адаптивной моделью (пмиам)

В БАИАМ информация в процессе идентификации получалась за счет входных и выходных параметров объекта. В ПЕИАМ также измеряются входные и выходные параметры, но также ведется поиск в пространстве параметров настраиваемой модели. Поиск является активным. Этим расширяются границы применимости данного алгоритма ПАИАМ, используют различные методы поиска, начиная от простого регулярного простого подбора пространства параметров и заканчивая более сложными градиентными методами, основанными на определении компонента градиента функции за счет тестовых сигналов (метод синхронного детектирования). В данном алгоритме возможна комбинация методов поиска. Простой метод поиска применяется для поиска района данного экстремума, пространства параметров модели целевой функции, и градиентный метод для уточнения экстремума данной целевой функции.

Алгоритмы ПАИАМ могут решать существенно более сложные задачи, чем БАИАМ. Общая структура ПАИАМ процесса. Для оптимизации химико-технологического процесса (ХТП) необходимо выбрать критерий, который отражает технологическую цель. Критерий может быть экономическим или технологическим. На основании выбранного критерия составляется целевая функция и ограничительная функция.

Ограничительная функция — зависимость показателей ХТП от параметров, влияющих на их значение.

При этом в целевую и ограничительную функции включается одинаковые аргументы. Задача оптимизации решается в том случае, если необходимо преимущественное улучшение показателей работы ХТП балансируя один (или второй) показатель против другого (или первого).

Любой ХТП по формальным признакам, действующим на него параметров можно представить следующей схемой.

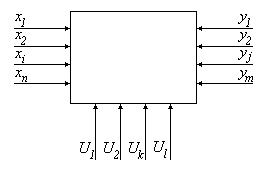
Рис. 49

где 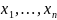— входные контролируемые параметры;

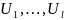— управляемые параметры:

— выходные параметры, которые являются суммарным действием входных и управляемых параметров.

Параметры представим в векторной форме:

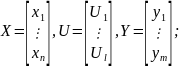
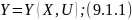
Выражение 9.1.1 — математическая модель данного ХТП.

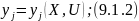
Выражение 9.1.2 — система уравнений данной математической модели.

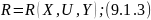
с учетом 9.1.1 получим:

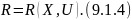
Решение задачи оптимизации представляется в виде зависимости управляющих воздействий от вектора пространственных координат :

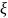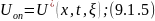
Для каждого необходимо найти такой вектор , который обеспечит экстремум критерия . Решение возможно только при наличии математической модели.

Различают две стадии оптимизации: статическая и динамическая. Статическая заключается в определении нового наилучшего состояния объекта, если это вызывается необходимостью при изменении вектора входных параметров .

Статическая оптимизация заключается в переводе объекта из одного установившегося состояния в другое.

Критерий оптимизации в этом случае может быть;

Без ограничения:

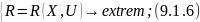
С ограничениями:

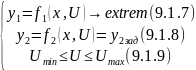
Решение задачи оптимизации будем иметь в виде:

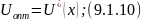
Статическая оптимизация применяется для оптимального управления такими непрерывными процессами, которые при определенном значении достигают установившегося значения за приемлемый промежуток времени.

Существует ряд процессов, которые характеризуются нестационарным режимом протекания процесса, который описывается динамическим выражением — динамическая оптимизация. Примеры: все периодические процессы химической технологии; критерий: за один цикл получить продукт максимального качества за минимальное время.

В данном случае функция оптимальности является критерием времени, который должен учитывать поведение объекта в течении всего периода нестационарной работы. Поэтому критерий оптимизации имеет интегральную форму;

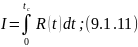
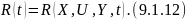
Задача динамической оптимизации решается следующим образом:

для каждого момента времени для любого значения вектора входных определяется вектор управляющих параметров , который обеспечивает оптимальное поведение объекта

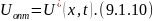
Выбор метода оптимизации (поиска ) зависит от постановки задачи и от вида математической модели. Для оптимизации применяются аналитические и численные методы.