3. Регулирование расхода жидких сред

Объект регулирования участок трубопровода г:

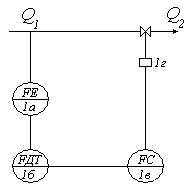
Рис. 41

где — коэффициент пропорциональности клапана;

— перемещение клапана.

Так как жидкость полностью заполняет сечение трубопровода, то изменение на ту же величину изменяет , то есть .

Запишем 7.3.1 в безразмерной форме:

где

Выражение 7.3.3 преобразуем по Лапласу при :

4. Регулирование расхода сыпучего материала

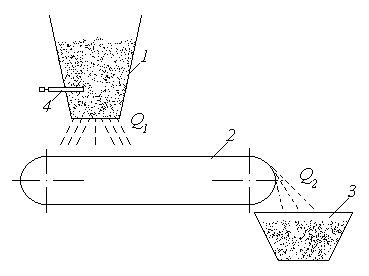
Рис. 42

4 — шибер (заслонка).

Лента конвейера перемещается со скоростью .

При равномерной загрузке ленты транспортера определяется как:

где — объем материала;

— рабочая длина от места сброса из бункера 1 в место сброса в бункер 3.

В момент времени мы увеличиваем степень открытия шибера, при этом получим:

В начальный период .

Для отрезка времени : .

Для отрезка времени : .

5. Регулирование концентрации вещества в смесителях. Регулирование концентрации вещества в смесителях

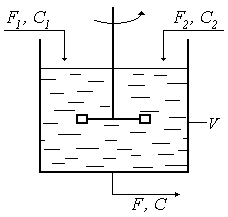
Рис. 43

— объемные скорости потоков;

— концентрации вещества.

— объём смесителя.

Предполагается, что .

Переменными величинами являются .

Для нахождения уравнения динамики объекта составим уравнение материального баланса по концентрациям веществ за время :

Данное уравнение является не линейным дифференциальным уравнением, поэтому приведем это уравнение, к линейному виду заменив все переменные величины суммой их значений в стационарном режиме к приращением:

Запишем уравнение 7.5.3 для стационарного режима:

Вычтем из 7.5.5 уравнение 7.5.6:

Так как приращение переменных малы, то и их произведения мало, то есть приблизительно равно нулю.

Выражение 7.5.8 представим в безразмерных величинах:

Разделим на коэффициент при :

6. Регулирование температуры в смесителях идеального перемешивания

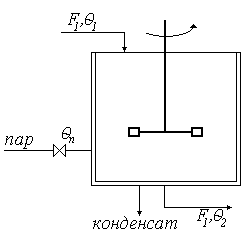
Рис. 44

где — линейная скорость;

— температура.

.

где — плотность жидкости;

— удельная теплоемкость жидкости;

— коэффициент теплоотдачи от пара;

— вес жидкости в смеси;

— тепловой поток, поступающий в смеситель с жидкостью:

— тепловой поток за счет теплообмена между паром и жидкостью;

— тепловой поток, уходящий из смесителя;

— накопление тепла.

Представим переменные величины как сумму в стационарном режиме и приращения:

Для нестационарного режима работы:

Приращение малы, следовательно, произведения приращений малы, то есть приблизительно равны нулю.

Вычтем из уравнения 7.6.4 уравнение 7.6.2:

Разделим все члены выражения 7.6.6 на коэффициент при :

где

Начальные условия:

Преобразуем по Лапласу уравнение 7.6.8: