3. Передаточная функция ректификационной колонны

Передаточная функция -той тарелки:

где входные величины:

— расход жидкости;

— расход паре;

, .

Выходные величины:

, .

С индексом “ ⁰ ” — стационарные значения, с индексом “ ’ ” — приращение параметра в переходном режиме.

Запишем 5.3.1 для стационарного режима:

Запишем 5.3.2 для стационарного режима:

Получим передаточную функцию по следующему каналу в этом режиме все остальные переменные принимаются в стационарном режиме, кроме данного входа:

, .

Решаем 5.3.1 для данных условий:

Запишем 5.3.2 для данных условий:

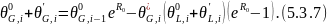
Вычитаем из 5.3.7 уравнение 5.3.4:

Вычитаем из 5.3.7 уравнение 5.3.5:

где

Перепишем 5.3.10 в виде:

С учетом 5.3.12 упростим 5.3.9:

Подставим 5.3.13 в 5.3.8:

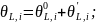
Вычитаем из 5.3.17 уравнение 5.3.5:

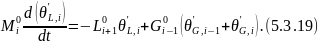
Вычитаем из 5.3.18 уравнение 5.3.5:

Подставляем 5.3.20 в 5.3.19:

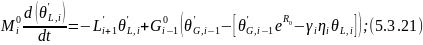
Канал

, — стационарные значения.

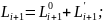
Запишем 5.3.1 стационарных условий:

Запишем уравнение 5.3.2:

Вычтем из 5.3.24 уравнение 5.3.4:

Преобразуем 5.3.26:

Так как приращения переменных принимаем равными небольшим переменным, следовательно, произведение небольших приращений приблизительно равно нолю.

Начальными условиями для 5.3.28 будут:

Преобразуем по Лапласу по времени уравнение 5.3.26:

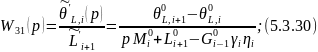
Канал

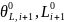, — стационарные значения.

Запишем 5.3.1 стационарных условий:

Запишем уравнение 5.3.1 для данных условий:

Вычтем из 5.3.32 уравнение 5.3.4:

Вычтем из 5.3.32 уравнение 5.3.5:

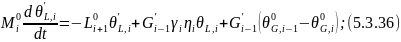
Преобразуем по Лапласу по времени 5.3.36:

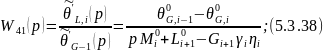
Процессы тепло- и массопередачи проходящие в кубе-испарителе и дефлегматоре протекают намного быстрее чем на тарелке, поэтому передаточная функция по каналам этих частей можно представить в виде усилительных звеньев для получения которых можно использовать вышеприведенные статические зависимости.

6. Математическое моделирование математических процессов

1. Математическая модель процесса химического превращения (кинетическая модель)

Протекание химической реакции можно описать следующим стехиометрическим уравнение:

— исходные компоненты реакции;

— продукты реакции;

— стехиометрические коэффициенты;

— стехиометрические коэффициенты.

Уравнение 6.1.1 можно представить в более общем виде:

Пусть в реакторе протекает -реакций:

в реакции участвуют веществ.

Уравнение 6.1.1 примет вид:

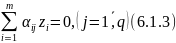
где 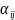— стехиометрический коэффициент -той реакции по -тому компоненту.

— для исходных компонентов;

— для продуктов реакции.

Если -тое вещество не участвует в -той реакции, то .

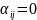Основной характеристикой химической реакции является её скорость. Скорость. Химической реакции по -тому компоненту называется изменение компонента в единицу времени:

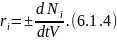
Зная скорость химической реакции по одному из компонентов можно определить скорость по остальным:

где — количество молей -того вещества участвующего в -той реакции;

— скорость стадии -той реакции.

По закону действующих масс:

где — константа скорости -той реакции;

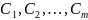— концентрации.

Общий порядок реакции равен;

где зависит от температуры:

где — предэкспоненциальный множитель, зависящий от свойств компонентов;

— энергия активации -той реакции;

Химические реакции по количеству стехиометрических уравнений описывающих их протекание подразделяются на простые и сложные.

Пример простых:

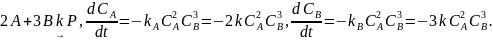
Константы скорости реакции по соответствующему компоненту равна константе стадии реакции на соответствующий стехиометрический коэффициент.

Сложные реакции делятся на параллельные, последовательные и смешанные и обратимые. Изменение концентрации -того вещества в сложной реакции равна скорости его образования (расходования) на всех стадиях в которых данное вещество участвует, то есть сложная реакция разделяется на отдельные стадии.

Пример:

1. Параллельная реакция:

2. Последовательная реакция:

3. Обратимая реакция:

4. Смешанная: