2. Противоточный кожухотрубчатый теплообменник

Направление оси принимаем по направлению первичного потока, а направление вторичного потока противоположно.

При математическом моделировании данного теплообменника уравнения 4.3.4 и 4.3.10 будут те же, а в уравнении 4.3.6 изменятся знаки при :

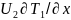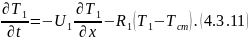
4. Математическая модель конденсатора (паровой теплообменник)

В этом теплообменнике пар, поступающий в него, полностью конденсируется. Температура пара определяется давлением в данном теплообменнике. Так как давление в замкнутом теплообменнике постоянно, то это означает. Что температура пара постоянная, то есть температура не изменяется по линейной координате (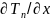 =0, ).

Математическая модель без учета тепловой инерции стенки будет иметь следующий вид:

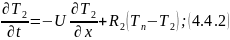
где — температура хладагента,

а .

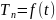Математическая модель с учетом накопления тепла в стенке:

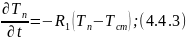
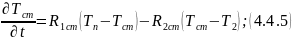
5. Передаточные функции теплообменных аппаратов

4.5.1 Конденсатор без учета накопления тепла в станке

Математическая модель имеет следующий вид:

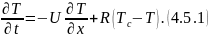
где 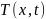— температура хладагента;

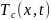— температура пара.

Начальные условия для уравнения 4.5.1:

Граничные условия:

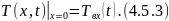
Структурная схема:

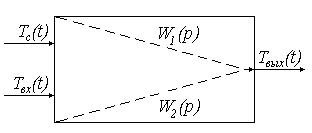
Рис. 33

Второе граничное условие:

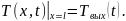
Преобразуем по Лапласу по времени при начальных условиях 4.5.2 уравнение 4.5.1:

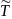, где символ преобразования по времени.

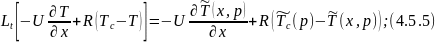
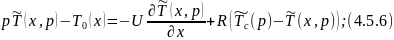
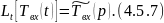
4.5.7 является граничным условием для 4.5.6.

Преобразуем по Лапласу по линейной координате уравнение 4.5.6 с учетом граничных условий 4.5.7:

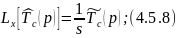
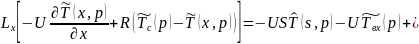
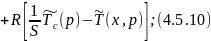
Прировняем 4.5.9 и 4.5.10:

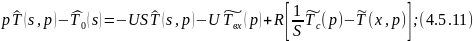
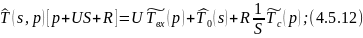
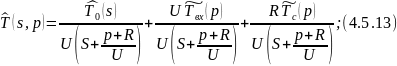
Применим обратное преобразование по Лапласу по линейной координате выражение 4.5.13:

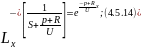
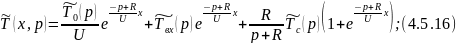
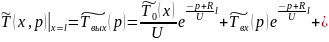
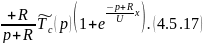
При значительной длительности режима :

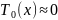4.5.2 Конденсатор с учётом накопления тепла в стенке

Математическая модель данного теплообменника имеет вид:

, ,

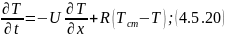
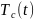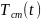
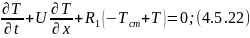
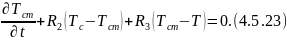
Начальные и граничные условия:

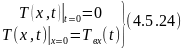
Преобразуем по Лапласу по времени 4.5.22 4.5.23:

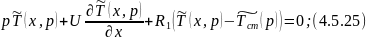
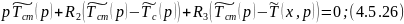
Преобразуем уравнение 4.5.25:

Преобразуем уравнение 4.5.26:

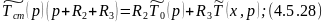
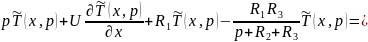
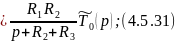
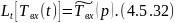
Уравнение 4.5.32 является граничным условием для 4.5.31.

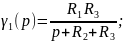
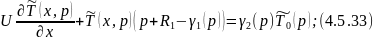
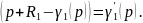
Преобразуем по Лапласу по линейной координате 4.5.33 при 4.5.32:

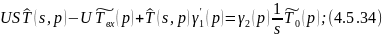
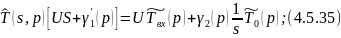
Произведем обратное преобразование по Лапласу по линейной координате уравнения 4.5.36:

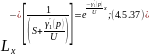
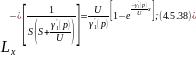
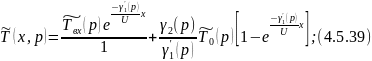
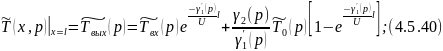
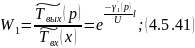
4.5.3 Кожухотрубчатый противоточный теплообменник

Математическая модель:

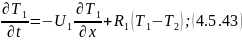
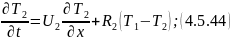
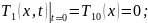
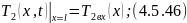
Преобразуем по Лапласу по времени при нулевых начальных условиях 4.5.43 и 4.5.44:

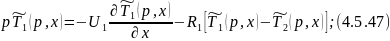
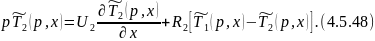
Преобразуем 4.5.47:

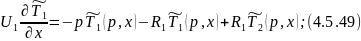
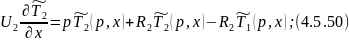
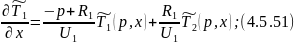
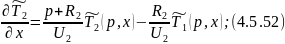
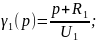
Для решения данной системы уравнений составим матрицу:

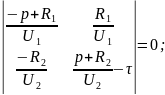
где — корни матрицы.

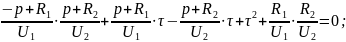
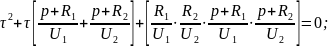
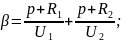
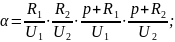
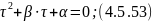
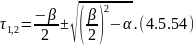
Решение уравнений 4.5.51 и 4.5.52 с учетом 4.5.54 примет следующий вид:

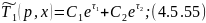
где , , 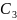, 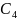— постоянные интегрирования, которые находятся из граничных условий.

Продифференцируем по уравнение 4.5.55:

:

:

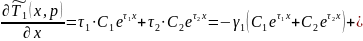
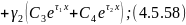
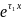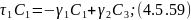
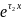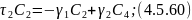
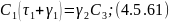
Получим граничное условие для 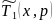из уравнения 4.5.55:

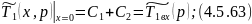
Из 4.5.63 определим :

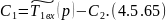
Подставляем 4.5.65 в 4.5.61:

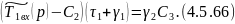
Из выражения 4.5.64 найдем :

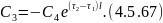
Подставляя 4.5.67 в 4.5.66:

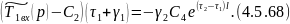
Умножаем левую и правую часть 4.5.68 на :

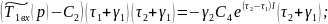
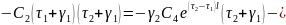
Выражение 4.5.62 домножим на :

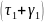Так как левые части уравнений 4.5.69 и 4.5.70 равны, то равны их правые части:

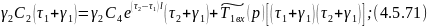
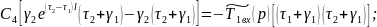
Подставляем 4.5.72 в 4.5.67:

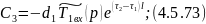
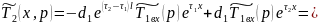
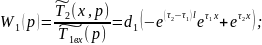
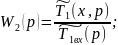
Для нахождения и необходимо использовать выражение 4.5.61 и 4.5.62.

Примечание: уравнения 4.5.51 и 4.5.52 нельзя преобразовывать по Лапласу по линейной координате, то есть они имеют различные граничные условия.