Модель идеального перемешивания
За структуру потока соответствующую модели идеального перемешивания принимают следующие:
Поток среды, поступающий в аппарат, мгновенно распределяется по всему объему аппарата и концентрация вещества в каждой точке аппарата и на его выходе одинакова.
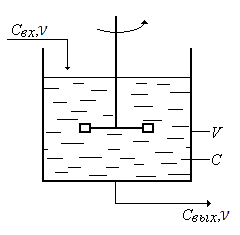
Рис. 18
где
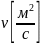— объемная скорость;
— объем
зоны идеального перемешивания;
Для
стационарного режима:
,
,
Для нестационарных режимов:
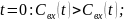
где
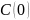— концентрация в установившимся режиме.
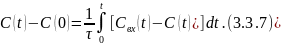
Продифференцируем 3.3.7 пот времени:
Преобразуем по Лапласу при нулевых начальных условиях выражение 3.3.9:
Решение
уравнения 3.3.8 зависит от вида
.
Если:
,
то
Выражение 3.3.11 называется F-кривой.
Рис. 19
,
то
Рис. 20
Если
при исследовании неизвестной структуры
потока, полученные экспериментальные
и
кривой совпадают с расчетными, то модели
можно отнести к модели идеального
перемешивания.
На
практике часто стремясь получить модель
идеального перемешивания, снабжаются
их мешалками. Наиболее лучшему режиму
идеального перемешивания соответствуют
ёмкостные аппараты, проточного типа
снабженные мешалками при небольшой
объемной скорости и при условии
.
Модель идеального вытеснения
За структуру потока соответствующую модели идеального вытеснения (МИВ) принимается поршневое течение вещества без перемешивания частиц в продольном направлении, при равномерном распределении концентрации вещества в сечении перпендикулярных направлению движения потока.
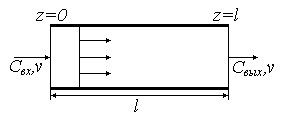
Рис. 21
где — линейная координата;
где — объемная скорость;
— линейная скорость потока;
— сечение
потока.
Для
вывода уравнения модели идеального
вытеснения выделим
-тую
элементарную ячейку, объемом
,
длинной
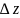и сечением
.
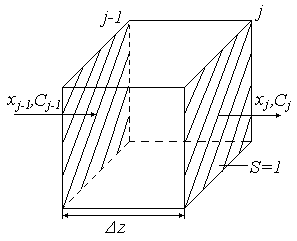
Рис. 21
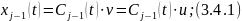
Для стационарных режимов:
Для нестационарных режимов:
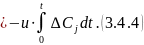
Разделим
3.4.4 на
:
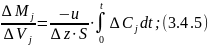
Так как не зависит от времени, введем его под знак интеграла:
Продифференцируем по времени левую и правую часть:
Ввиду поршневого течения вещества данное уравнение справедливо для всего потока:
Так как это уравнение является уравнением в частных производных, то МИВ является моделью с распределенными параметрами.
3.4.10 преобразуем по Лапласу по времени, получим:
Уравнение 3.4.12 имеет решение:
полагаем
z=0:
.
Таким образом, 3.4.13 примет вид:
полагаем
:
Построим и кривые:
Рис. 22
Рис. 23
Модели
идеального вытеснения наиболее
соответствуют трубчатые вещества при
турбулентном течении вещества и
Диффузионные модели
Согласно теории массообмена диффузия бывает молекулярная и конвективная. Молекулярная — процесс проходит на микроуровне, конвективная — перенос вещества осуществляется его частицами, то есть процесс проходит на макроуровне.
Однопараметрическая диффузионная модель. Перемешивание частиц в продольном направлении характеризуется коэффициентом
,Двухпараметрическая диффузионная модель. Данный поток характеризуется коэффициентом продольного перемешивания и коэффициентом радиального перемешивания
.