
- •«Моделирование объектов и систем управления отрасли»
- •Введение
- •Методы моделирования объектов и систем управления
- •Физическое моделирование объектов и систем управления
- •Метод подобия
- •Метод аналогий
- •Математическое моделирование химико-технологических процессов
- •Сущность, свойства и этапы математического моделирования химико-технологического процесса
- •Основные виды математических моделей химико-технологических процессов
- •Блочный принцип разработки математических моделей химико-технологических процессов
- •Основные подходы получения математических моделей химико-технологических процессов
- •Классификация экспериментальных методов. Виды математических моделей.
- •Модели динамики (статистические) химико-технологического процесса
- •Определение динамических характеристик химико-технологических процессов при активном эксперименте
- •Проведение эксперимента по снятию переходных функций
- •Обработка результатов эксперимента по снятию переходных функций
- •Получение динамических характеристик объекта по переходным функциям
- •Определение динамических характеристик объектов при входных воздействиях в виде случайных сигналов
- •Свойства и характеристики стационарных случайных процессов
- •Постановка эксперимента по определению статистических характеристик процессов
- •Определение динамических характеристик объектов и систем управления методом моментов
- •Применение метода модулирующих функций для определения динамических характеристик объектов и су
- •Получение модели статики объектов и су
- •Определение моделей статики (уравнения регрессии) при пассивном эксперименте
- •Регрессионный анализ в матричной форме
- •Получение модели статики при активном эксперименте
- •Детерминированные (аналитические) модели химико-технологических процессов
- •Использование уравнений материального и теплового баланса для описания стационарных и нестационарных режимов протекания химико-технологических процессов
- •Модели структуры потоков, как основа построения математических моделей гидромеханики химико-технологического процесса
- •Модель идеального перемешивания
- •Модель идеального вытеснения
- •Диффузионные модели
- •Однопараметрическая диффузионная модель (одм)
- •Двухпараметрическая диффузионная модель
- •Ячеечная модель
- •Математическое описание тепловых процессов
- •Прямоточные кожухотрубчатые теплообменники
- •Противоточный кожухотрубчатый теплообменник
- •Математические модели теплообменников с учетом накопления тепла в стенке
- •Прямоточный кожухотрубчатый теплообменник
- •Противоточный кожухотрубчатый теплообменник
- •Математическая модель конденсатора (паровой теплообменник)
- •Передаточные функции теплообменных аппаратов
- •4.5.1 Конденсатор без учета накопления тепла в станке
- •4.5.2 Конденсатор с учётом накопления тепла в стенке
- •4.5.3 Кожухотрубчатый противоточный теплообменник
- •Математическое моделирование массообменных аппаратов
- •Математическая модель процесса газоабсорбции
- •Математическая модель процесса ректификации
- •Передаточная функция ректификационной колонны
- •Математическое моделирование математических процессов
- •Математическая модель процесса химического превращения (кинетическая модель)
- •Математическая модель химического реактора идеального перемешивания
- •Математическая модель реактора идеального вытеснения
- •Передаточные функции химических реакторов
- •Передаточная функция реактора идеального перемешивания простого типа
- •Реактор идеального вытеснения
- •Математическое моделирование динамики типовых контуров регулирования технологических параметров объекта
- •Свойства, характеристики и классификация объектов регулирования
- •Регулирование уровня в резервуарах
- •Регулирование расхода жидких сред
- •Регулирование расхода сыпучего материала
- •Регулирование концентрации вещества в смесителях. Регулирование концентрации вещества в смесителях
- •Регулирование температуры в смесителях идеального перемешивания
- •Регулирование состава смеси в реакторе с мешалкой
- •Методы и алгоритмы идентификации динамических систем
- •Общая классификация задач идентификации
- •Постановка задачи идентификации
- •Идентификация непрерывных объектов в классе моделей с дискретным временем
- •Задача непараметрической идентификации
- •Задачи параметрической идентификации
- •Безпоисковые алгоритмы идентификации с адаптивной моделью (баиам)
- •8.6.1 Общая структура баиам в пространстве сигналов
- •8.6.2. Общая структура баиам с дискретным временем и операторным описанием
- •Оптимизация химико-технологических с использованием математических моделей
- •Постановка задач оптимизации
- •Поисковые модели идентификации с адаптивной моделью (пмиам)
- •Аналитические методы оптимизации
- •Метод классического анализа функций
- •Метод неопределенных множителей Лагранжа
- •Линейное программирование
- •Нелинейное программирование
- •Численные методы оптимизации. Постановка задачи оптимизации
- •Реализация методов оптимизации в пакете MatLab (toolbox)
- •Оптимизация (минимизация) функции
- •9.5.5. Использование метода наименьших квадратов для решения задач оптимизации
Детерминированные (аналитические) модели химико-технологических процессов
Использование уравнений материального и теплового баланса для описания стационарных и нестационарных режимов протекания химико-технологических процессов
Согласно блочному принципу разработки математических моделей сложных химико-технологических процессов (ХТП) исследуются и моделируются элементарные процессы (блоки) протекающие на различных уровнях ХТП.
В основе математического описания протекания данных элементарных процессов лежат уравнения материального и теплового баланса.
Обобщенное уравнение материального баланса:
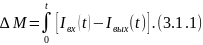
где
 — накопление вещества за время [0,t];
— накопление вещества за время [0,t];
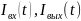 — входной
и выходной потоки.
— входной
и выходной потоки.
Данное уравнение описывает нестационарный режим работа ХТП. Стационарный режим описывается уравнением материального баланса:
(приход вещества)=(расходу вещества)

Аналогичные уравнения можно записать для теплового баланса:
(приход тепла)-(расход тепла)=(накопление тепла)
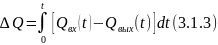
где
 — изменение энтальпии объекта за время
[0,t];
— изменение энтальпии объекта за время
[0,t];
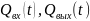 — входной
и выходной потоки.
— входной
и выходной потоки.
Уравнение 3.1.3 описывает нестационарный режим работы ХТП.
Стационарный режим описывается:
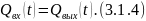
Приведенные уравнения описывают элементарные процессы, протекающие на макроуровне.
Для описания стационарных режимов применяются конечные уравнения и их системы. Для описания нестационарных режимов применяется однородные дифференциальные уравнения (линейные и нелинейные) и их системы, дифференциальные уравнения в частных производных.
Модели структуры потоков, как основа построения математических моделей гидромеханики химико-технологического процесса
Любой химико-технологический процесс (ХТП) сопровождается перемещениями потоков, которые могут быть однофазными и многофазными, поэтому необходимо получить математическое описание этих потоков, то есть гидродинамику. Однако, гидродинамика многофазных потоков сложна.
При моделировании гидродинамики сложных ХТП будем прибегать к упрощенному варианту свойств многофазных потоков, сводя эти свойства к более простому варианту.
Структура потоков определяется степенью перемешивания частиц вещества данного потока, которая определяет поле концентрации.
По степени перемешивания можно выделить следующие типовые структуры потоков и соответствующие им математические описания:
— модель идеального перемешивания;
— модель идеального вытеснения;
модели, описывающие гидродинамик реальных потоков:
— диффузия модели;
— ячеечные модели;
— комбинированные модели.
Универсальным описанием данных моделей является однородные дифференциальные уравнения или дифференциальные уравнения в частных производных отражающие изменение концентрации.
Требования к моделям:
Должна быть обеспечена возможность расчета коэффициентов модели;
С помощью их необходимо исследовать гидродинамику потоков и оптимизировать гидродинамичный режим.
При моделировании гидродинамики сложных ХТП изучается основные свойства, производятся некоторые упрощения этих свойств, и эти свойства сводятся к одной из типовых структур потоков с известной моделью.
Если в аппарате несколько потоков, то для каждого из потоков разрабатывается материальное описание.
