
- •Какие события называются независимыми? Докажите, что если события
- •Сформулируйте и докажите формулу полной вероятности. Приведите пример ее применения.
- •Сформулируйте и докажите формулу Байеса. Приведите пример ее применения.
- •Используя интегральную приближённую формулу Лапласа, выведите формулу для оценки отклонения относительной частоты события а от вероятности p наступления a в одном опыте.
- •Докажите, что коэффициент корреляции случайных величин х и у удовлетворяет условию .
- •Докажите, что для непрерывной случайной величины, распределенной по показательному закону с параметром , математическое ожидание .
- •Cформулируйте определение начальных моментов случайной величины. Докажите, что если х и у – независимые случайные величины, то
- •Пусть - начальные, а - центральные моменты некоторой случайной величины.
- •Найдите эксцесс равномерного распределения на отрезке [а,b].
- •Сформулируйте и докажите неравенство Чебышева.
- •Используя н-во Чебышева, сформулируйте и док-те «правило трех сигм» для произвольной св X.
- •Сформулируйте и докажите теорему Чебышева для бесконечной последовательности сл. Величин с одинаковыми математическими ожиданиями и дисперсиями, ограниченными одним и тем же числом.
- •Сформулируйте и докажите теорему Бернулли (закон больших чисел).
- •Используя центральную предельную теорему, обоснуйте интегральную формулу Лапласа.
- •Докажите, что для генерального распределения с математическим ожиданием m и конечной дисперсией σ2 выборочное среднее является несмещенной и состоятельной оценкой m.
- •Пусть x1,…Xn – выборка из распределения с дисперсией 2. Док-те, что - несмещенная оценка 2.
- •Выведите формулу для дисперсии выборочного среднего бесповторной выборки.
Докажите, что коэффициент корреляции случайных величин х и у удовлетворяет условию .
Определение: Коэффициентом корреляции
двух случайных величин называется
отношение их ковариации к произведению
средних квадратических отклонений этих
величин:
![]() .
.
.
.
Доказательство: Рассмотрим случайную
величину Z =
![]() .
Вычислим ее дисперсию
.
Вычислим ее дисперсию
![]() .
Поскольку левая часть неотрицательна,
то правая неотрицательна. Следовательно,
.
Поскольку левая часть неотрицательна,
то правая неотрицательна. Следовательно,
![]() ,
|ρ|≤1.
,
|ρ|≤1.
Как вычисляется дисперсия в случае непрерывного распределения с плотностью f (x)? Докажите, что для случайной величины X с плотностью
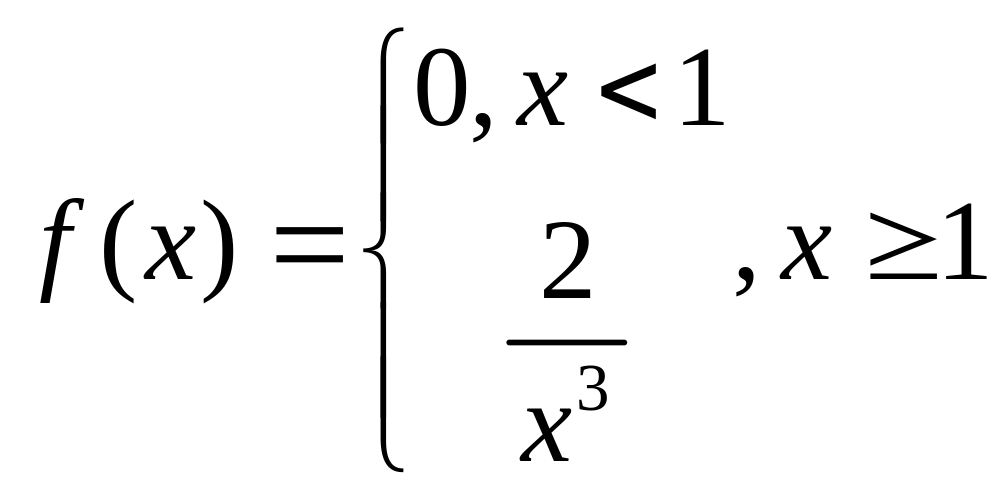 дисперсия
D(X) не существует,
а математическое ожидание M(X
) существует.
дисперсия
D(X) не существует,
а математическое ожидание M(X
) существует.
Дисперсия абсолютно непрерывной случайной величины X с функцией плотности f(x) и математическим ожиданием m = M(X) определяется таким же равенством, как и для дискретной величины
![]() .
.
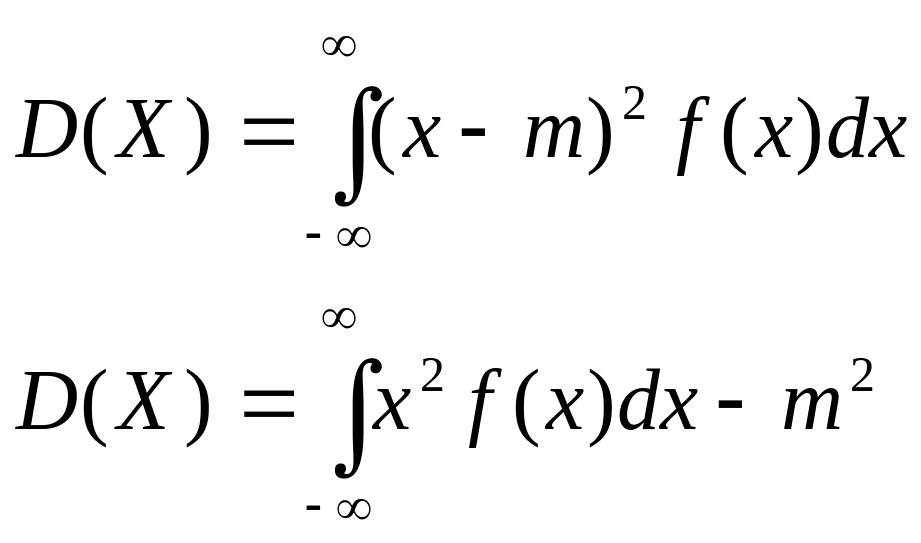
В случае когда абсолютно непрерывная случайная величина X сосредоточена на промежутке [a, b],

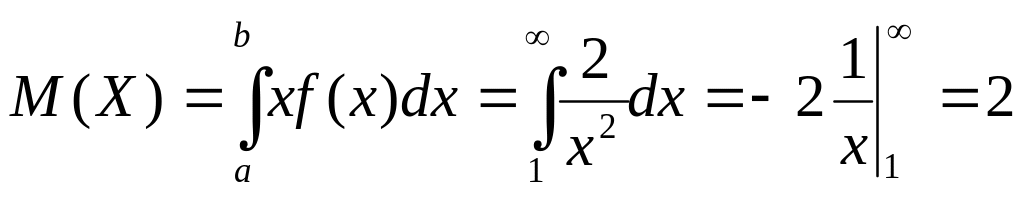
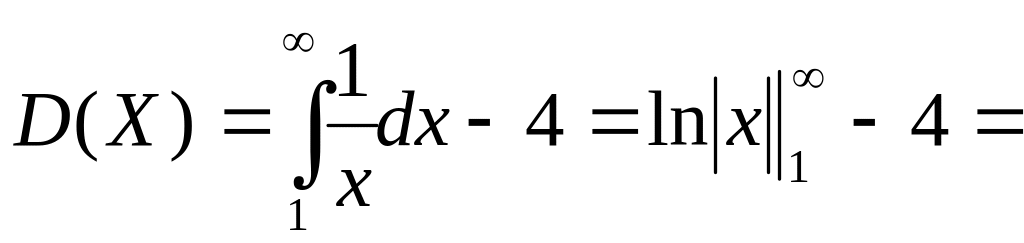 ∞
- интеграл расходится, следовательно,
дисперсия не существует.
∞
- интеграл расходится, следовательно,
дисперсия не существует.
Докажите, что для нормальной случайной величины Х с функцией плотности распределения
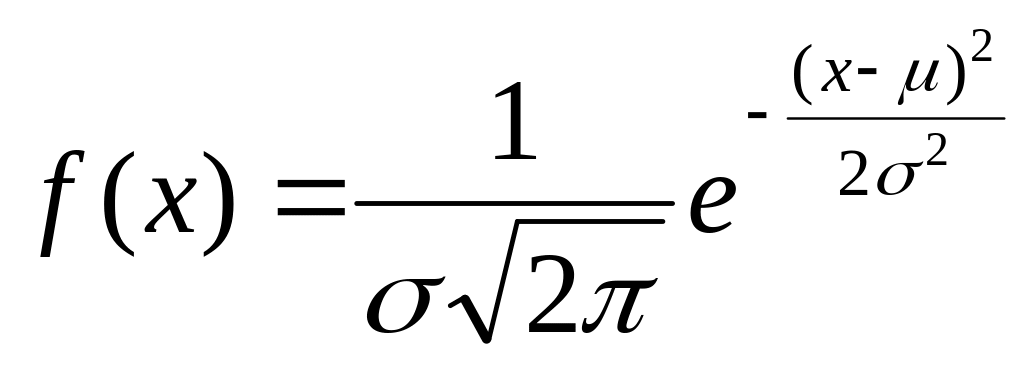 математическое ожидание М(Х) = μ.
математическое ожидание М(Х) = μ.
Формула
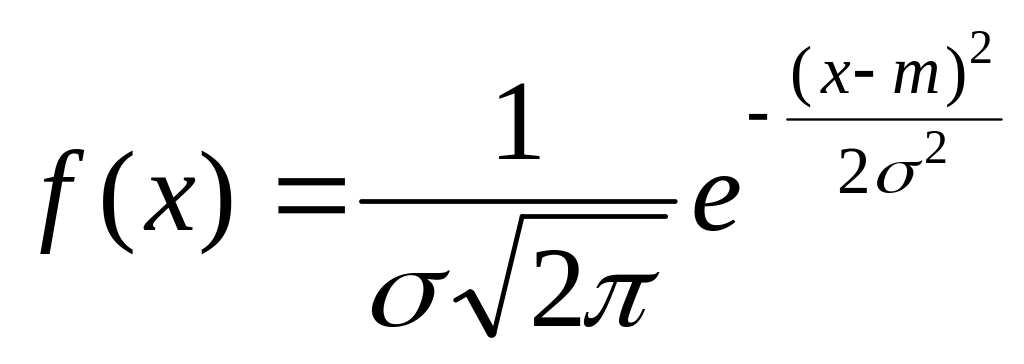 описывает
плотность нормального распределения
вероятностей непрерывной с.в..
описывает
плотность нормального распределения
вероятностей непрерывной с.в..
Докажем, что μ есть математическое ожидание.
По определению математического ожидания непрерывной с.в.,
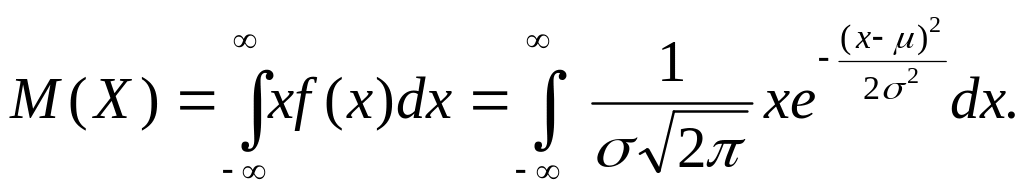 Введем
новую переменную
Введем
новую переменную
![]() .
Отсюда
.
Отсюда
![]() .
Приняв во внимание, что новые пределы
интегрирования равны старым, получим
.
Приняв во внимание, что новые пределы
интегрирования равны старым, получим
![]()
Первое из слагаемых равно нулю ввиду
нечетности подинтегральной функции.
Второе из слагаемых равно μ
(интеграл Пуассона
![]() ).
).
Итак, M(X)=μ, т.е. математическое ожидание нормального распределения равно параметру μ.
Докажите, что для нормальной случайной величины Х с функцией плотности распределения диспресия D(X) = σ2.
Формула описывает плотность нормального распределения вероятностей непрерывной с.в..
Докажем, что
![]() -
среднее квадратическое отклонение
нормального распределения.
-
среднее квадратическое отклонение
нормального распределения.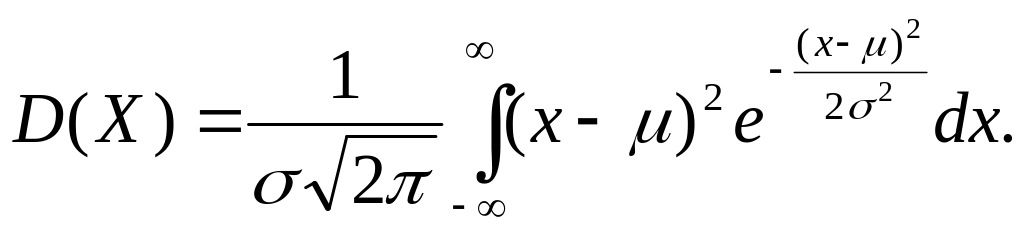 Введем новую переменную z=(х—μ)/
.
Отсюда
Введем новую переменную z=(х—μ)/
.
Отсюда
![]() .Приняв
во внимание, что новые пределы
интегрирования равны старым, получим
.Приняв
во внимание, что новые пределы
интегрирования равны старым, получим
![]() Интегрируя по частям, положив u=z,
Интегрируя по частям, положив u=z,
![]() найдем
найдем
![]() Следовательно,
Следовательно,
![]() .Итак,
среднее квадратическое отклонение
нормального распределения равно
параметру
.
.Итак,
среднее квадратическое отклонение
нормального распределения равно
параметру
.
Докажите, что для непрерывной случайной величины, распределенной по показательному закону с параметром , математическое ожидание .
Говорят, что случайная величина X, принимающая только неотрицательные значения, распределена по показательному закону, если для некоторого положительного параметра λ>0 функция плотности имеет вид:
![]()
Для нахождения математического ожидания воспользуемся формулой
M(X)=
![]()
Найдем интеграл методом
интегрирования по частям, полагая u
= x,
dv =
e–λxd(λx),
так что du =
dx,
v =
–e–λx.
Получим 
Таким образом, M(X)=![]() .
.
Cформулируйте определение начальных моментов случайной величины. Докажите, что если х и у – независимые случайные величины, то
Начальным моментом порядка k (k принадлежит N) случайной величины Х называется мат.ожиданием k-й степени Х.
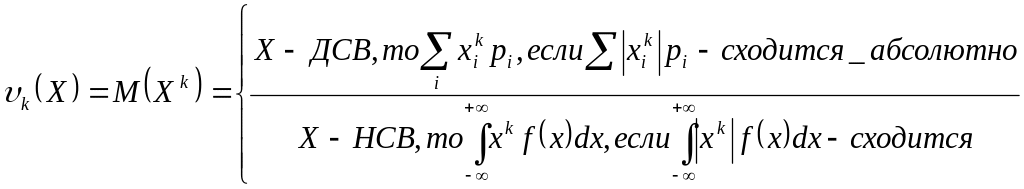
Центральным моментом порядка k СВ Х называется мат.ожидание k-й степени отклонения:
![]()

![]()
Теорема: если Х и У независимые СВ,
то
![]()
Док-во:
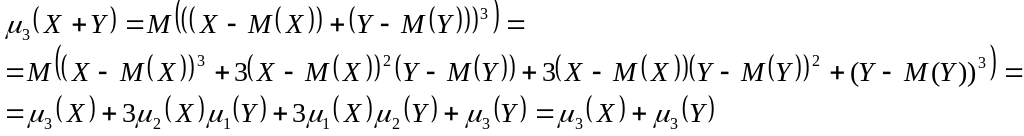
-по теореме умножения математического ожидания для независимых величин.
