3.3. Задача о выборочном контроле

Пусть имеется партия изделий общим объемом N штук. Известно, что в этой партии M изделий бракованные. Найти вероятность того, что среди наугад выбранных n изделий ровно m из них будут бракованными.

Общее количество элементарных исходов равно числу сочетаний Cⁿ_N – количество различных наборов при выборе n изделий из N без возвращения и без учета порядка.

Количество различных наборов при выборе m бракованных изделий из M без возвращения и без учета порядка равно числу сочетаний C^m_M.

Количество различных наборов при выборе n – m годных изделий из N – M без возвращения и без учета порядка равно числу сочетаний C^n–m_N–M.

Количество благоприятных исходов равно произведению C^m_MC^n–m_N–M.

Отсюда следует, что искомая вероятность равна отношению: P = C^m_MC^n–m_N–M / Cⁿ_N.

Задачи

№14. Ящик содержит 10 деталей, среди которых 3 бракованных. Найти вероятность того, что из наудачу отобранных 5 деталей окажется не более одной бракованной.

По условию данной задачи нас интересует вероятность наступления сложного события B, которое реализуется при наступлении любого из следующих двух простых событий: среди отобранных деталей нет ни одной бракованной (А₀); среди отобранных деталей имеется ровно одна бракованная (А₁). В силу того, что простые события А₀ и А₁ являются несовместными, то искомая вероятность сложного события В = А₀ + А₁ вычисляется по формуле сложения несовместных событий: P(В) = P(А₀ + А₁) = P(А₀) + P(А₁). Вероятности простых событий А₀ и А₁ находятся по формулам:

P(А₀) = ; P(А₁) = ;

P(В) = P(А₀) + P(А₁) = 7/24 + 21/40 = (35 + 63)/120 = 98/120 ≈ 0,816667.

4. Условная вероятность, независимость событий

4.1. Условная вероятность

Определение Условной вероятностью наступления события A при условии, что произошло событие B, называется число:

P(A|B) = P(AB)/P(B), [P(B) ≠ 0]. (4)

П ример 5 Пусть при бросании игральной кости выпадение четного числа очков является событием A = {2, 4, 6}, а выпадение числа очков более трех – событием B = {4, 5, 6}. Игральная кость подбрасывается один раз. Известно, что выпало более трех очков. Какова вероятность того, что выпало четное число очков?

При подбрасывании кубика произошло событие B. При этом событие A может как наступить (выпало 4 или 6 очков), так и не наступить (выпало 5 очков). Но нас интересует именно наступление события A. Следовательно, мы должны рассматривать одновременное наступление событий A и B, т.е. их произведение – AB = {4, 6}:

P(A|B) = P(AB)/P(B) = (2/6) / (3/6) = 2/3.

4.2. Независимость

Понятие независимости является ключевым в теории вероятностей и поэтому очень важно правильно его понимать. Без ясного понимания этого понятия, все дальнейшие положения теории вероятностей будут трактоваться неправильно.

Определение События A и B называются независимыми, если P(AB) = P(A)P(B).

Отсюда следует, что: P(A|B) = P(AB)/P(B) = [P(A)P(B)]/P(B) = P(A), (P(B) ≠ 0)

П ример 6 Точка с координатами (x; y) бросается наудачу в единичный квадрат  со сторонами, параллельными осям координат. Доказать, что для любой заранее выбранной точки единичного квадрата с координатами (x₀; y₀)   события: A = {x ≤ x₀} и B = {y ≤ y₀} являются независимыми.

|| = 11 = 1, |A| = x₀1 = x₀, P(A) = |A| / || = x₀.

|B| = y₀1 = y₀, P(B) = |B| / || = y₀.

P(AB) = |AB| / || = x₀y₀, но P(A)P(B) = x₀y₀ → события A и B независимы.

П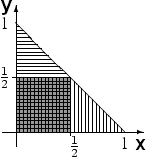 ример 7 Точка с координатами (x; y) бросается наудачу в треугольник с вершинами (1; 0), (0; 0), (0; 1). Доказать, что события A = {x ≤ 1/2} и B = {y ≤ 1/2} зависимы.

|| = (11)/2 = 1/2, |A| = ¼ + 1/8 =3/8, P(A) = |A| / || = 3/4.

|B| = ¼ + 1/8 = 3/8, P(B) = |B| / || = 3/4.

P(AB) = |AB| / || = (1/4) / (1/2) = ½, но P(A)P(B) = 9/16 → события A и B зависимы.

З амечание 1 Несовместные события A и B будут независимыми только в вырожденном случае, когда P(A) = 0 или P(B) = 0.

В невырожденном случае, когда P(A) ≠ 0 и P(B) ≠ 0 несовместные события не могут быть независимыми. Зависимость между ними следует из простой причинно-следственной связи: т.к. A  , то при наступлении события A обязательно наступает событие , т.е. событие B обязательно не наступает, а это уже зависимость!

Это же можно сформулировать иначе: в невырожденном случае независимые события просто обязаны пересекаться, т.е. обязаны быть совместными.

Замечание 2 Если события A и B независимы, то независимыми являются также события: A и , B и Ẵ, Ẵ и (без доказательства).

Замечание 3 По аналогии с определением независимости двух событий A и B может показаться, что при бóльшем числе событий A₁, A₂, …, A_n достаточно выполнение одного только равенства P(A₁A₂…A_n) = P(A₁)P(A₂)…P(A_n), чтобы считать эти события независимыми. Однако из этого равенства вовсе не следует, что, например, события A₁ и A₂ являются независимыми. Независимостью нескольких событий следует считать такое их свойство, при котором любые мыслимые комбинации произведений этих событий являются независимыми между собой.

Определение События А₁, А₂, …, А_n называются независимыми в совокупности, если для любого 1 ≤ k ≤ n и любого набора различных между собой индексов 1 ≤ i₁, i₂…i_k ≤ n выполняется равенство: P(A_i1A_i2…A_ik) = P(A_i1)P(A_i2)…P(A_ik).

Замечание 4 Если события А₁, А₂…А_n независимы в совокупности, то они попарно независимы, т.е. любые два события А_i, А_j независимы, но обратное утверждение неверно.

Пример 8 (С.Н.Бернштейн) Рассмотрим правильный тетраэдр, 3 грани которого окрашены, соответственно, в красный, синий и зеленый цвета, а четвертая грань окрашена во все три этих цвета. Пусть событие A означает, что при бросании тетраэдра он упал на грань, содержащую красный цвет, событие B – синий цвет и событие C– зеленый цвет.

Вероятность наступления каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность одновременного наступления любых двух из них равна 1/4, так как только одна грань является многоцветной. А так как (1/2) (1/2) = 1/4, то все события являются попарно независимыми. Но вероятность одновременного наступления всех трех событий тоже равна 1/4, а не 1/8 как следовало бы для независимых событий, то есть события не являются независимыми в совокупности.