2.4. Геометрическое определение вероятности
Если пространство элементарных исходов содержит бесконечное множество элементов и ему можно поставить в соответствие некоторое геометрическое пространство, а вероятность каждого события зависит только от меры этого события, а не от его положения, то говорят, что на этом пространстве определена геометрическая вероятность. При этом вероятность каждого события А есть отношение меры события А к мере пространства элементарных исходов .
Под мерой понимается:
в одномерном пространстве – длина;
в двумерном пространстве – площадь;
в трехмерном пространстве – объем.
Таким образом, геометрическая вероятность означает, что:
P(A) = mes(A) / mes() = |A| / ||. (3)
Б
росание
монеты на стол (босяцкая французская
забава)
Стол разграфлен на квадраты со стороной A и на него игрок бросает монету диаметром d (d < A). Если монета пересекает хотя бы одну из линий, то игрок ее проигрывает. Какова вероятность выигрыша игрока?
Легко видеть, что игрок выигрывает, если центр монеты попадает во внутрь квадрата со стороной B = A – d. Вероятность этого события равна:
P = B2 / A2 = (A – d)2 / A2 = (1 – d/A)2.
Для равенства шансов выиграть/проиграть необходимо чтобы:
(1 – d/A)2 = 0,5; 1 – d/A = √2/2; d/A = 1–√2/2; d = (1–√2/2)A ≈ 0,2929A.
И
гла
де
Бюффона
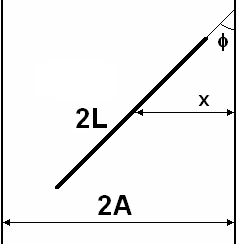
Стол разграфлен параллельными линиями на расстоянии 2A и на него бросается игла длиной 2L (L < A). Какова вероятность события B, означающего, что игла пересечет какую-либо линию?
Положение иглы можно характеризовать следующими двумя параметрами:
х – расстояние от центра иглы до ближайшей линии;
φ – угол между осью иглы и направлением линий.
Случайный характер положения иглы означает, что параметр х может равновероятно принимать любые значения от 0 до A независимо от параметра φ, который может равновероятно принимать любые значения от 0 до . Тогда пространство элементарных исходов можно представить прямоугольником со сторонами A и , а событие B – областью под кривой:
||
=
A;
x
≤ Lsin(φ);
|B|
=
= –Lcos(φ)
=
–L[–1
– 1] = 2L.
Т.о., вероятность пересечения иглы с одной из линий равна: P(A) = |B| / || = 2L / (A).
Иногда вместо геометрических мер (длина, площадь или объем) приходится использовать временные интервалы с теми же идеями, что и в задачах о геометрической вероятности.
З
адача
о встрече
Пусть два человека обедают в столовой с 12 до 13 часов. Каждый из них приходит в произвольный момент времени и обедает не более 10 минут. Какова вероятность их встречи?
Пусть x – время прихода первого в столовую, а y – время прихода второго (12 ≤ x, y ≤ 13).
Пространство элементарных исходов можно представить множеством точек квадрата, стороны которого лежат на координатных осях. Начало координат соответствует времени 12 часов, а стороны квадрата простираются по координатным осям до точки, соответствующей времени 13 часов.
Очевидно, что встреча обедающих состоится только при условии их появления в столовой, с разностью во времен не более 10 минут. При этом возможны следующие три случая:
1. Первый и второй пришли одновременно: y – x = 0 (точки на прямой линии y = x).
2. Первый пришел раньше второго: y – x 1/6 (область с горизонтальной штриховкой).
3. Второй пришел раньше первого: x – y 1/6 (область с вертикальной штриховкой).
Легко видеть, что искомая вероятность равна отношению площади заштрихованной области к площади квадрата. Площадь квадрата равна единице, а площадь заштрихованной области можно определить как разность между площадью единичного квадрата и суммой площадей двух угловых треугольников (они составляют квадрат со стороной равной 5/6):
P = 1 – (5/6)(5/6) = 1 – (25/36) = 11/36.
3. ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ
В теории вероятностей часто приходится иметь дело с задачами, в которых необходимо подсчитывать либо число возможных способов совершения каких-либо действий, либо количество "шансов". Задачи такого типа называются комбинатόрными. При их решении следует использовать следующие универсальные правила и принципы:
Правило произведения Пусть требуется выполнить одновременно два каких-либо действия. Если первое действие можно выполнить k способами, а второе – m способами, то выполнить эти действия можно k + m способами.
Правило суммы Пусть требуется выполнить одно из каких-либо двух действий, взаимно исключающих друг друга. Если первое действие можно выполнить k способами, а второе – m способами, то выполнить одно из этих двух действий можно k + m способами.
Примечание. Эти результаты легко распространяются на любое количество действий, элементы которых участвуют в подобных комбинациях.
Задачи
№4. У двух аудиофилов имеется 5 и 7 CD-дисков соответственно. Сколькими способами они могут обменяться двумя дисками? (5·4·7·6 = 20·42 = 840).
№5. Подсчитайте количество всех четных трехзначных чисел (9·10·5=450).
№6. Подсчитайте количество всех трехзначных чисел, у которых все цифры различные (9·9·8 = 648: числа без нуля – 9·8·7 = 504, числа с одним нулем – 9·8·1+9·1·8=144; 504+144=648).
№7. Руководителю надо назначить двух дежурных, работающих в одном и том подразделении. Всего имеется три подразделения, в которых трудятся 3, 5 и 10 работников соответственно. Сколько вариантов назначения дежурных имеется у руководителя? (3·2 + 5·4 + 10·9 = 6 + 20 + 90 = 116).
№8. Сколькими способами можно разместить на шахматной доске восемь ладей так, чтобы они не били друг друга (64·49·36·25·16·9·4·2·1 = 3 251 404 800).
Принцип Дирихле Если в n клетках сидит n+1 кроликов, то найдётся клетка, в которой сидят по крайней мере два кролика.
Задачи
№9. В темной комнате в ящике комода лежат вперемешку 100 пар белых и 100 пар черных носков. Какое наименьшее количество носков надо взять, чтобы образовалась одна одноцветная пара? (n + 1, где n – количество цветов).
Факториал Факториалом натурального числа n называется число: n! = n·(n–1)·(n–2)·...·2·1, причем 0! = 1 по определению.
Бинома Ньютона Ckn = n!/[k!(n – k)!] определяет значение k-го коэффициента в биноминальном разложении: (a + b)n = C0nan + C1nan–1b + + Cknan–kbk + ... + Cn–1nabn–1 + Cnnbn .
Ckn = Cn–kn – симметрия; Ckn + Ck+1n = Ck+1n+1 – равенство Паскаля;
C0n + C1n +...+ Cnn = 2n; (C0n)2 + (C1n)2 +...+ (Cnn)2 = Cn2n .