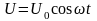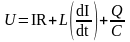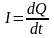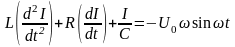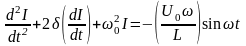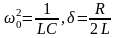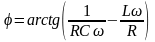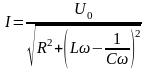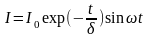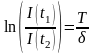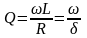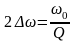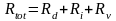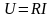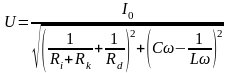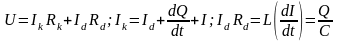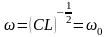Міністерство освіти і науки України

Національний технічний університет України

«Київський політехнічний інститут»

Фізико-технічний інститут

Протокол

Лабораторна робота з фізики №8

RLC-коло

Виконав:

студент групи

ФЕ-11

Закандаєв Т.Ю.

Прийняли:

Тараненко Ю.О.

Маркіна Т.М.

Київ 2012 р.

Ключові поняття:

Коливальне коло (tuned circuit), послідовний контур (series-tuned circuit), паралельний контур (parallel-tuned circuit), опір (resistance), ємність (capacitance), індуктивність (inductance), конденсатор (capacitor), котушка індуктивності (coil), зсув фаз (phase displacement), добротність (Q-factor), ширина резонансної кривої (band-width), опір втрат (loss resistance), згасання (damping).

Мета роботи:

Дослідження залежності сили струму та напруги від частоти в паралельному та послідовному коливальному контурі. Визначення Q- фактора та ширини лінії коливального кола для різних величин активних (R), та реактивних (LC) навантажень:

1. Послідовне з'єднання

а) резонансу сили струму за відсутністю активного опору;

б) резонансу сили струму за наявністю активного опору;

в) резонансу напруги за відсутністю активного опору;

2. Паралельне з'єднання

а) резонансу напруги за відсутністю активного опору;

б) резонансу сили струму за відсутністю активного опору.

Література:.

1. Сивухин Д. В. Общий курс физики. Т.3, Электричество и магнетизм. - М.: Наука, 1977. - гл. 10, п.п. 122-124, 126-131.

2. Парселл Э. Электричество и магнетизм. БКФ, т.2. - М.: Наука, 1971. - гл.8.

Теоретичне підґрунтя.

Будь-яке коло змінного струму можна розглядати як сукупність омічного опору, конденсатора та котушки індуктивності. Схему, що містить всі три означені елементи називають коливальним колом.

К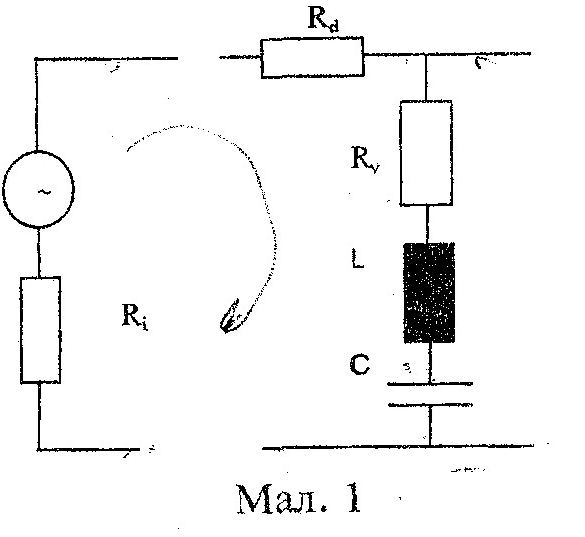 оливальне коло уявляє собою приклад коливальної системи із одним ступенем волі і служить не тільки основою для утворення передаючих та приймаючих приладів, але й дуже зручною та ясною моделлю для вивчення резонансних процесів. В даній роботі передбачається знайомство із основними характеристиками коливальних контурів різної архітектури.

Розглянемо спочатку еквівалентну схему послідовного коливального контуру (Мал. 1). Вона складається із генератора змінного струму з внутрішнім опором R_i та ввімкнутих послідовно омічного опору конденсатора R_d конденсатора C, котушки індуктивності L. Крім того, на схемі вказано опір втрат R_v, який відтворює неминучі омічні втрати в котушці, конденсаторі, та дротах.

Вхідна напруга від генератора змінюється за гармонічним законом з частотою :

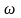(1)

Згідно із законом Кірхгофа, ця напруга дорівнює сумі напруг на конденсаторі, котушці та резисторі:

(2)

де І - сила струму, Q - заряд на конденсаторі.

Продиференціюємо рівняння (2) і скористаємось тим, що за визначенням струм дорівнює похідній від заряду за часом:

(3)

Тоді після підстановки (3) в (2) отримуємо диференціальне рівняння для струму:

(4)

Рівняння (4) зручніше аналізувати, якщо переписати його у стандартному вигляді:

(4’)

де введено позначення:

(5)

За відсутності зовнішньої сили (U₀=0) в контурі можливі згасаючі коливання.

При вмиканні генератора (зовнішньої сили) в контурі виникають перехідні процеси, які залежать від початкових умов. Але нас цікавить тільки стаціонарний режим, коли струм коливається із частотою примусової сили. В цьому випадку рішення рівняння (5) має вигляд:

(6)

де фаза коливань 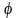визначається за формулою:

(7)

а амплітуд:

(8)

З виразу видно, що за частоти , яка визначається співвідношенням (5), амплітуда коливань максимальна. Ця частота називається резонансною. При наявності у конденсатора та індуктивності омічного опору R, вона відрізняється від власної частоти контура, різниця тим більша, чим більше згасання

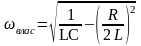
Зручною характеристикою відносного згасання в коливальному контурі є так звана добротність Q, або Q-фактор (не плутати з зарядом!). Вона тим більша, чим менше згасання і таким чином характеризує якість контура. Для осцилятора з частотою добротність визначається як відношення енергії, що накопичена в контурі в розрахунку на один період коливання до середньої кількості розсіяної енергії. Інакше можна сказати, що добротність - це добуток 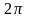та кількості коливань, протягом яких енергія коливань зменшиться в e разів.

Для RLC-кола добротність можна визначити двома способами.

Перший: загальну поведінку контуру у відсутності зовнішніх сил можна описувати як:

(9)

тобто коливання з амплітудою, яка зменшується із часом. Добротність Q контуру буде обчислюватись як 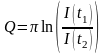, де t₁ – t₂ час проходу струму через максимуми коливання.

Якщо ми будемо вважати, що на протязі цього часу період (T), чи частота не змінюється, обчислення спрощуються:

Тобто добротність характеризує відношення періодів коливання електричного струму та його згасання. Якщо 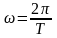, з (5) випливає:

(10)

Зворотню величину, 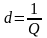називають фактором втрат.

З іншого боку, добротність простіше уявляти та вимірювати як залежність амплітуди коливань (7) від частоти примусової сили (резонансна крива). Як вже відзначалось, ця крива має максимум. Цей максимум тим більший і тим вужчий, чим більша добротність контура. Ширину резонансної лінії характеризують відстанню 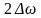між точками, амплітуда яких менша в 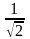від резонансної амплітуди. З (8), (10) легко вивести, що:

(11)

Повернемось тепер до нашого контура. Загальний опір його дорівнює:

(12)

Омічний опір визначається безпосередньо за номіналом (або за допомогою тестера), а внутрішній опір генератора та опір активних елементів можна розраховувати, вимірюючи одночасно струм та напругу:

(13)

Пам'ятайте, що до попередніх формул входить величина U₀ - напруга на генераторі без навантаження.

Тепер розглянемо еквівалентну схему паралельного коливального контуру (Мал. 2). У паралельному контурі опір втрат на конденсаторі дуже великий (кілька сот МОм), і їм можна знехтувати. А втрати в контурі виникають здебільшого за рахунок котушки. Навіть за резонансу у котушці також відбуваються втрати струму. Оскільки струми у котушці та конденсаторі за резонансу однакові, то RLC-коло має суто активний опір. Тому логічно визначити опір втрат у паралельному контурі, вимірюючи значення U та І.

Ц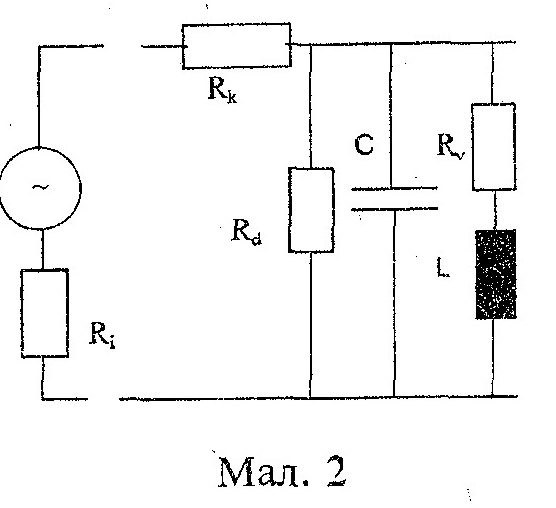 ей активний опір має бути під’єднаний послідовно конденсатору та індуктивності. Але активний опір конденсатора складає близько 100 МОм, і ним можна знехтувати. Як буде видно з результатів, виміряне значення опору втрат індуктивності R_v складатиме близько 1,5 кОм. Цей опір втрат, одначе, не дорівнює опору котушки з постійним струмом. У нашому випадку R_L=0.2 Ом та може бути виключений з подальшого розгляду. Якщо врахувати у сумі провідності елементів, одержуємо:

(14)

де 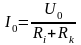. Формула (14) отримується за допомогою правил Кірхгофа:

(15)

та припущення, що при 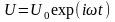струм індуктивності виглядатиме як .

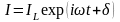Резонанс настає при частоті:

(16)