2 Этап.

Шаг 1. Определение координат эталонного образца.

В каждом столбце матрицы выделить максимальный элемент

Таким образом сформирована строка - эталонный вариант программного обеспечения.

Шаг 2. Нахождение расстояний до эталонного образца.

Расстояние от каждого варианта программного обеспечения до эталона рассчитывается с учетом коэффициентов иерархии критериев по следующей формуле:

Шаг 3. Формирование таблицы расстояний до эталона.

Таблица имеет следующий вид:

Таблица расстояний до эталона

Место (ранг) вариантам программного обеспечения присваивается в зависимости от степени близости к эталонному образцу.

Ниже приведен, пример распечатки исходных данных, промежуточных и окончательных результатов.

Исходная матрица

ПРИМЕР

Исходные данные Вариант №

1.Этап. Расчет матрицы стандартизированных значений

ПО
1	18	54	10	6	70
2	23	58	10	5	80
3	17	40	7	2	50
4	21	60	8	8	55
5	19	48	7	9	60

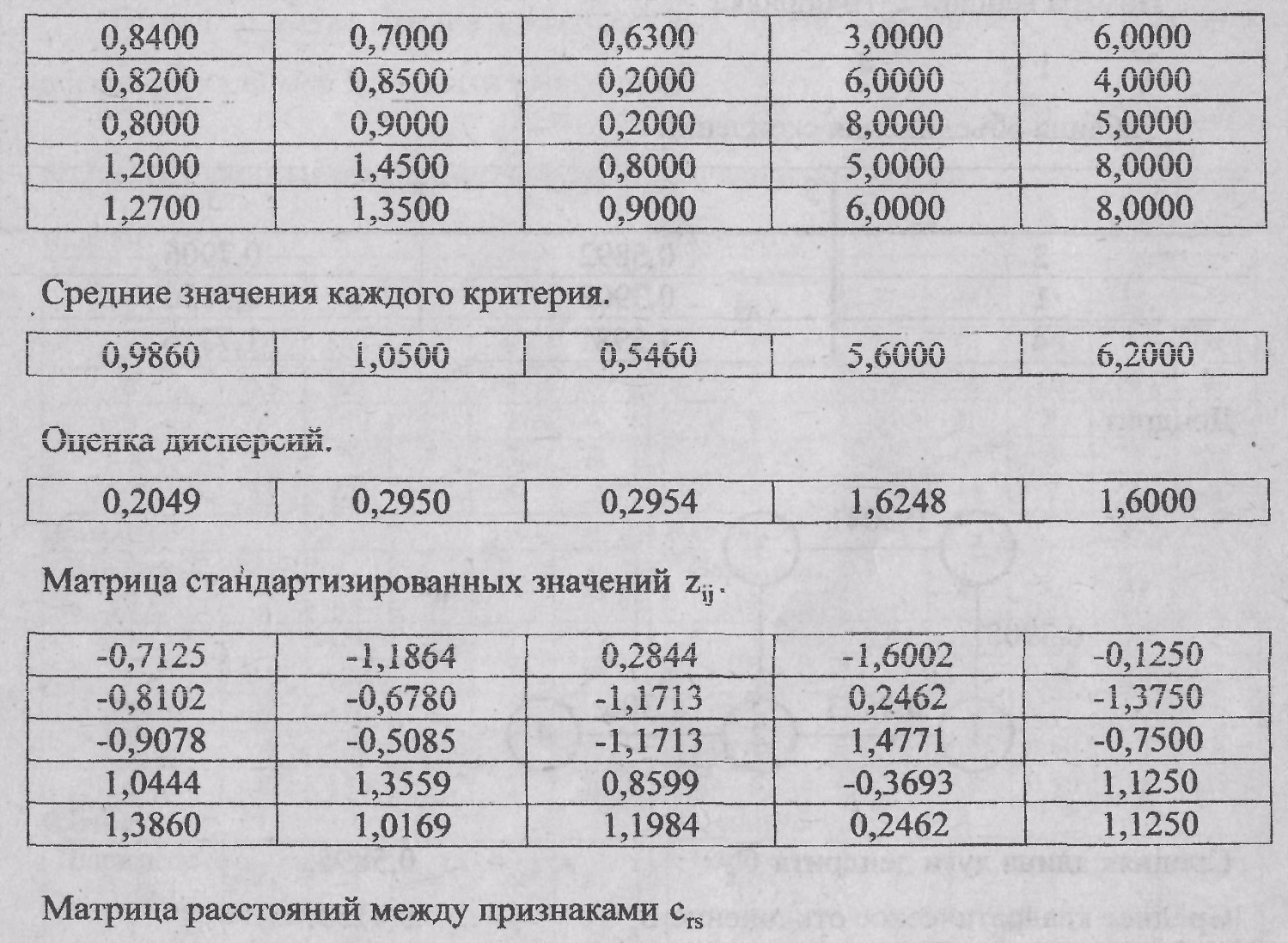
Шаг1. Определяем среднее значение каждого критерия

19,6	52	8,4	6	63

Проводим оценку дисперсий по формуле

2,154	7,266	1,356	2.449	10,770

Составляем матрицу стандартизированных значений

-0,742	0,275	1,179	0	0,649
1.578	0,825	1,179	-1,632	1,578
-1,207	-1.651	-1,032	-0,408	-1,207
0,649	1,1001	-0,294	0,816	-0,742
-0,278	-0,5504	-1,032	1.224	-0,278

Проверяем правильность составления матрицы по формуле

; 1) -0,742+1,5781-1,207+0,649-0,278=0 2)….=0…

Шаг2. Расчет матрицы расстояний между критериями

0	0,644	1,033	1,660	0,880
0,644	0	0,837	1,476	0,935
1,033	0,837	0	1,789	0,497
1,660	1,476	1,789	0	1,792
0,880	0,935	0,497	1,792	0

Шаг 3. Построение таблицы ближайших соседей

Номер критерия	Расстояние	Номер ближайшего соседа
1	0,644	2
2	0,644	1
3	0,497	5
4	1,476	2
5	0,497	3

Номера вершин 1- го порядка (по минимальным расстояниям):

3 и 5

Номера вершин 2 –го порядка:

1; 2; 4 .

Шаг4. Построение скоплений

Скоплениями считаем группу близких к друг-другу по расстоянию критериев.

Таблица объединения скоплений

	3	5
1	1,033	0,880
2	0,837	0,935
4	1,792	1,792

Дендрит

Средняя длина дуги дендрита:

.

С

реднее квадратичное отклонение

Критическое расстояние: =0,666+2 =0,941.

С

умма длин расстояний, меньших критическому по каждому критерию

(из матрицы расстояний между критериями)

1,524

2,417

1,33

0

2.31

1) 0,880+0,644=1,524; 2)…

Коэффициенты значимости критериев определяются как отношение к максимальной сумме (2.417) длин расстояний остальных сумм

0.631

1

0,550

0

0,956

Этап 2

Коэффициенты эталонного объекта

(из матрицы стандартизированных значений)

1,578

1,100

1,179

1,224

1.578

За эталонный элемент принимаем максимальный элемент в столбцах матрицы стандартизированных значений .

Таблица расстояний до эталона:

Номер проекта	Расстояние до эталона	Место
1	1.333	3
2	0,165	4
3	2,860	5
4	1,580	2
5	1,987	1

Вывод с точки зрения предлагаемых критериев вариант программного обеспечения №2 является наилучшим, так как расстояние до эталона у него минимально.

3