Некоммерческое акционерное общество

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра компьютерных технологий

Организация вычислительных систем и сетей

Методические указания к выполнению лабораторных работ

для студентов всех форм обучения

специальности 5В070400– «Вычислительная техника и программное обеспечение»

Алматы -2012

СОСТАВИТЕЛИ: Т.Т. Коржымбаев, Г.С. Нурмагамбетов «Организация вычислительных систем и сетей»

Методические указания к выполнению лабораторных работ для студентов всех форм обучения специальности 5В070400 – «Вычислительная техника и программное обеспечение». – Алматы: АИЭС, 2012. – 65 с

Методические указания предназначены для выполнения в компьютерном классе лабораторных работ по дисциплине «Организация вычислительных систем и сетей». Для каждой лабораторной работы даны краткие методические указания и упражнения для индивидуального выполнения. Перед выполнением лабораторной работы студент должен ознакомиться с методическими указаниями, изучить материалы по соответствующей теме и ответить на контрольные вопросы. После завершения лабораторной работы студент обязан представить преподавателю отчет в электронном виде.

Методические указания предназначены для студентов специальности 5В070400 – «Вычислительная техника и программное обеспечение» всех форм обучения.

Библиография – 6 назв.

Рецензент: канд. техн. наук. доц. Б.М.Шайхин

Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2012 г.

© НАО «Алматинский институт энергетики и связи» на 2012 г.

Содержание

1 Лабораторная работа № 1.

Разработка алгоритма и микропрограммы арифметической операции над

числами с фиксированной ,плавающей точкой и двоично-десятичными

кодами.

2 Лабораторная работа № 2.

Исследование логических основ цифровых автоматов.

3 Лабораторная работа № 3.

Программирование

разветвляющегося процесса.

Система команд

4 Лабораторная работа № 4.

Исследование конвейерной обработки

5 Лабораторная работа № 5

Подпрограммы и стек

6 Лабораторная работа № 6

Программирование внешних устройств

7 Лабораторная работа № 7

Изучение программы PacketTracer . Изучение интерфейса командной строки Cisco ios.

8 Лабораторная работа № 8

Изучение орбит ИСЗ с помощью программы “Orbitron”

Лабораторная работа №1

Разработка алгоритма и микропрограммы арифметической операции над числами с фиксированной ,плавающей точкой и двоично-десятичными кодами.

Цель работы: Произвести операции сложения являющихся базовой с использованием машинных кодов с использованием программной модели АЛУ.

Теоретическая часть

Набор арифметических операций составляют операции сложения, вы­читания, умножения и деления. Операция сложения является ба­зовой, так как она входит в состав операций умножения и деле­ния, а вычитание вообще выполняется как сложение с учетом знаков операндов (при использовании машинных кодов).

Алгоритм сложение целых двоичных чисел с ФТ производится в следу­ющем порядке:

1. Операнды представляются в обратном или дополнительном коде. Обычно используют ДК.

2. Сложение операндов производится поразрядно, начиная с младшего разряда.

3. В каждом разряде выполняются сложение двух цифр слагаемых и перенос из младшего разряда в соответствии с правилами двоичной арифметики.

4. Знаковые разряды участвуют в сложении наряду с цифровыми разрядами. Знак результата получается автоматически.

5. При сложении чисел в ДК перенос из знакового разряда отбрасывается. (При сложении чисел в ОК перенос из знакового разряда прибавляется к младшему разряду суммы.)

6. Если слагаемые представлены в ДК, то результат сложения получается также в ДК.

7. При сложении чисел с одинаковыми знаками возможно пе­реполнение разрядной сетки.

Сложение и вычитание чисел с ПТ. Особенностью сложения и вычитания чисел с ПТ является то, что в общем случае операнды могут иметь различные порядки. Суммировать разряды мантиссы можно только тогда, когда они имеют одинаковый вес, поэтому перед суммированием мантисс необходимо выровнять порядки. При этом могут быть потеряны младшие разряды мантиссы. Для уменьшения погрешности выполняется округление результата. После суммирования результат может оказаться ненормализован­ным, в этом случае необходима его нормализация.

С учетом этих особенностей сложение чисел с ПТ выполняется : в следующем порядке: подготовительный этап, выравнивание порядков, сложение мантисс, заключительный этап.

Алгоритм сложение целых двоичных чисел с ПТ производится в следу­ющем порядке:

1. Сравниваются порядки (характеристики) исходных чисел путем их вычитания Δ p=p₁-p₂ . При выполнении этой операции определяется, одинаковый ли порядок имеют исходные слагаемые.

2. Если разность порядков равна нулю, то это значит, что одноименные разряды мантисс имеют одинаковые веса (двоичный порядок). В противном случае должно проводиться выравнивание порядков.

3. Для выравнивания порядков числа с меньшим порядком сдвигается вправо на разницу порядков Δ p. Младшие выталкиваемые разряды при этом теряются.

4. После выравнивания порядков мантиссы чисел можно складывать (вычитать) в зависимости от требуемой операции. Действия над слагаемыми производятся в обратном или дополнительном коде по общим правилам.

5. Порядок результата берется равным большему порядку.

6. Если мантисса результата не нормализована, то осуществляются нормализация и коррекция значений порядка.

Арифметические операции над двоично-десятичными кодами чисел

При обработке больших массивов экономической информации пере­воды чисел из десятичной системы в двоичную и обратно могут тре­бовать значительного машинного времени. Некоторые образцы ЭВМ поэтому имеют или встроенные, или подключаемые блоки, которые обрабатывают десятичные целые числа в их двоично-десятичном пред­ставлении. Действия над ними также приводятся к операции алгебра­ического сложения отдельных цифр чисел, представленных дополни­тельными кодами в соответствии с табл.

Существует несколько алгоритмов сложения двоично-десятичных кодов десятичных чисел. Приведем один из алгоритмов сложения, ко­торый получил довольно широкое распространение.

1. Сложение чисел начинается с младших цифр (тетрад) и произво­дится с учетом возникающих переносов из младших разрядов в старшие.

2. Знак суммы формируется специальной логической схемой по знаку большего слагаемого.

3. Для того чтобы при сложении двоично-десятичных цифр возни­кали переносы, аналогичные при сложении чисел в десятичном пред­ставлении, необходимо проводить так называемую десятичную кор­рекцию. Для этого к каждой тетраде первого числа прибавляется до­полнительно по цифре 6₁₀=0110₂, что позволяет исключить шесть не­используемых комбинаций (1010—1111)₂, так как они кодируют шестнадцатеричные цифры А—F (числа 10—15₁₀).

4. После операции суммирования осуществляется корректировка суммы. Из тех тетрад суммы, из которых не было переносов, изыма­ются ранее внесенные избытки 6₁₀=0110₂. Для этого проводится вто­рая коррекция. Операция вычитания заменяется, как и обычно, опе­рацией сложения с числом -6, представленным дополнительным ко­дом 1010₂, но только в тех разрядах, в которых отсутствовали пере­носы. При этой второй коррекции переносы из тетрад блокируются.

5. Операция вычитания реализуется достаточно своеобразно. По общему правилу сложения (см. п. 1—4) к тетрадам числа с большим модулем прибавляются дополнительные коды тетрад другого числа. При этом первая коррекция не проводится, так как в дополнениях тет­рад она учитывается автоматически. Знак результата определяется по знаку числа с большим модулем.

При сложении над двоично-десятичными числами со знаком используются обратный или дополнительный код. Для получения ОК к каждой тетраде при­бавляется двоичное число 0110, а затем все цифровые тетрады инвертируются. Дополнительный код получают из обратного пу­тем прибавления единицы к младшей тетраде.

Задание 1

Пример 1. Сложить числа А₁₀ = -2 и В₁₀ = -9 с одинаковыми знаками (без

переполнения).

А₂= − 0010→ А₂^пк = 1 0010→ А₂^ок =1 1101→ А₂^дк= 1 1110

+ +

В₂= −1001→ В₂^пк = 1 1001→ В₂^ок = 1 0110→ В₂^дк =1 0111

А₂ ^дк +В₂^дк= С₂^дк = 11 0101→ С₂^пк =1 1011;

С₂ = −1011, С₁₀=−11.

При сложении чисел с одинаковыми знаками возможно по­лучение результата, значение которого больше величины 2^n-1, где n — разрядность слагаемых. При этом результат не укладывается в отведенных для него разрядах, поэтому такая ситуация называет­ся переполнением разрядной сетки.

Пример 2. Сложить числа А₁₀ = -13 и В₁₀ = -6 с одинаковыми знака­ми (с переполнением).

А₂ = −1101 → А₂^пк = 1 1101→ А₂^ок = 1 0010 → А₂^дк = 1 0011

+ +

В₂ = -0110 → В₂^пк = 1 0110 → В₂^ок = 1 1001 → В₂^дк = 1 1010

А₂ ^дк +В2^дк= С₂^дк= 10 1101→С₂^пк =0 1101;

С₂ = + 1101, С₁₀=+13.

Одним из признаков переполнения является отличие знака суммы от знака слагаемых. Иногда при сложении используется модифицированный дополнительный код (МДК), в котором для знака числа отводится два разряда. В этом случае признаком пере­полнения являются различные значения знаковых разрядов сум­мы. Если переполнение не возникает, то значения знаковых раз­рядов совпадают. Рассмотрим примеры сложения чисел в МДК.

Пример 3. Сложить числа А₁₀ = +11 и В₁₀ = +8 (сумма больше 0).

А₂= + 1011→ А₂^пк = 0 1011 → А₂^ок = 0 1011 → А₂^мдк = 00 1011

+ +

В₂ =+ 1000 → В₂^пк = 0 1000 → В₂^ок = 0 1000 → В₂^мдк = 00 1000

А₂ ^дк +В₂^дк = С₂^мдк = 01 0011

Переполнение! Различные значения знаковых разрядов суммы.

Так как при сложении в дополнительном коде учитываются знаки чисел, то вычитание чисел можно заменить сложением в соответствии с соотношением

А-В = А + (–В).

Таким образом, вычитание заменяется сложением уменьшае­мого с вычитаемым, взятым с обратным знаком.

Пример 4. Произвести вычитание чисел А₁₀= −3 и B₁₀ = +15 (с пере­полнением).

А₂= − 0011→ А₂^пк= 1 0011 → А₂^ок=1 1100→ → → → → А₂^дк= 1 1101

+ +

В₂=+1111 → В₂^пк= 0 1111→ (− В)₂^пк = 1 111→ (− В)₂^ок=1 0000 →

→ (− В)₂^дк =1 0001

______

А₂ ^дк +В₂^дк= С₂^дк= 10 1110;

С₂^пк = 0 1101 С₂=+1101? Переполнение!

Признаком переполнения в данном случае являются различные зна­чения знаковых разрядов разности.

Задание 2

Пример 5. Выполнить сложение чисел с ПТ в ДК, если А₁₀ = −15⁵/₈;

А₂ =−1111.101; А_ПТ = −0.1111101х10⁺¹⁰⁰.

В₁₀ = + 16¹/₄; В₂ = +10000.01; В_ПТ =+0.1000001х10⁺¹⁰¹ .

(М_А)^пк= 1 1111101; (М_А)^дк = 1 0000011; (Р_А)^пк=0 100; (Р_А)^дк= 0 100; (М_В)^пк =

0 1000001; (М_В)^дк = 0 1000001;

(Р_В)^ПК = 0 101; (Р_В)^дк = 0 101; (−Р_В)^дк=1 011.

Вычислим разность порядков:

(Р_А)^ДК = 0 100

+

(−Р_В )^дк=1 011

______________

(ΔР)^ДК = 1 111 →(ΔР)^ПК =1 001→ (ΔР)₂ =−001→(ΔР)₁₀ =−1.

Разность порядков не равна нулю, выравнивание порядков необхо­димо. Разность порядков меньше нуля, число А имеет меньший порядок. Сдвигается мантисса числа А.

Мантисса числа А после сдвига: (М_А)^дк = 1 1000001 |1.

(В освобождающиеся разряды мантиссы заносится значение знаково­го разряда. Старший из выдвигаемых разрядов сохраняется в дополни­тельном разряде регистра суммы.)

Порядок суммы (Р_А+В)^ДК = (Р_В)^ДК = 0 101.

Выполним сложение мантисс: (М_А)^дк = 1 1000001 |1

+

(М_в)^дк = 0 1000001 |0

___________

(М_А)^дк+ (М_В)^дк= (М_А + М_В)^дк = 10 0000010 |1. Нормализация наруше­на справа.

Мантисса суммы сдвигается влево на пять разрядов.( не влево а вправо от сидящего)

Мантисса суммы после сдвига: (М_А + М_В)^дк = 0 1010000 |0

Округление. + |1

=___________

Мантисса суммы после округления: (М_А + М_В)^дк = 0 1010000.

Порядок суммы после нормализации: (Р_А+В)^ДК = 0 101 + 1 011=0 000. Результат: (М_А + М_В)^пк = 0 1010000 → (М_А + М_В)₂ = + 0.1010000.

(Р_А+В)^ДК = 0 000 → (Р_А+В)₂ = + 000.

Сумма: (А + В)_ПК = +0.1010000 х 10⁺⁰⁰⁰ →(А + В)₂ = +0.101 →(А+В)₁₀ =+⁵/_8.

Точный результат: −15⁵/₈ + 16¹/₄ = +⁵/_8.

При выполнении операции вычитания знак вычитаемого изменяется на противоположный, далее операция продолжается как сложение.

Пример 6. Определить разность чисел, представленных в форме с ПТ. Операцию выполнить с использованием МДК.

А₁₀ = −5³/₄; А₂ =−101.11; А_пт = −0.10111х10⁺⁰¹¹.

В₁₀ = + 3⁵/₈; В₂ = +11.101; В_пт =+0.11101х10⁺⁰¹⁰ .

(М_А)^пк= 1 10111; (М_А)^мдк = 11 01001; (Р_А)^пк=00 011; (Р_А)^мдк= 00 011; (М_В)^пк =

0 11101; (М_В)^мдк =00 11101; (−М_В)^мдк = 11 00011.

(Р_В)^пк = 00 010; (Р_В)^мдк = 00 010; (−Р_В)^мдк=11 110.

Вычислим разность порядков:

(Р_А)^мдк = 00 011

+

(−Р_В )^мдк=11 110

________

(ΔР)^мдк = 00 001 →(ΔР)^пк =00 001→ (ΔР)₂ =+001→ΔР)₁₀ =+1.

Разность порядков не равна нулю, выравнивание порядков необхо­димо. Разность порядков больше нуля, число В имеет меньший порядок. Сдвигается мантисса числа В.

Мантисса числа (−В) после сдвига: (−М_В)^мдк =11 10001|‌1.

Порядок разности (Р_А-В)^мдк = (Р_А)^мдк = 00 011.

Выполним сложение мантисс: (М_А)^мдк =11 01001|0

+

(−М_В)^мдк= 11 10001|1

___________________

(М_А)^мдк + (−М_В)^мдк= (М_А − М_В)^мдк = 0 11010|1. Нормализация на­рушена слева.

Мантисса разности сдвигается вправо на один разряд. Мантисса разности после сдвига: (М_А − М_В)^мдк = 11 01101|0 Округление. + |1

_______________________

Мантисса разности после округления: (М_А − М_В)^мдк =11 01101.

Порядок разности после нормализации: (Р_А-В)^мдк = 00 011 + 00 001 =

= 00 100.

Результат: (М_А – М_В)^пк = 11 10011 → (М_А − М_В)₂ = −0.10011.

(Р_А-В)^МДК = 0 100 → (Р_А-В)₂ = +100.

(А − В)_ПТ = −0.10011 х 10⁺¹⁰⁰ → (А- В)₂ = −1001.1 →(А− В)₁₀ = −9¹/₂.

Точный результат: −5³/₄ − 3⁵/₈ = −9³/_8.

Погрешность возникла при

сдвиге мантиссы числа В при выравнива­нии порядков.

Задание 3

Пример 7. Сложить два числа А_ю= 177; В₁₀=418.

Пример 8

Определить сумму чисел в двоично-десятичном коде, если

А₁₀ = –183; B10 = 924.

A_2–10 = – 0001 1000 0011; B_2–10 = + 1001 0010 0100

(A_2–10)^ПК = 1 0001 1000 0011 (B_2–10)^пк = 0 1001 0010 0100

+ 0110 0110 0110 Прибавление кода 0110

(A_2–10)^ОК = 1 0111 1110 1001

1 1000 0001 0110 Инверсия

+ 0001 Прибавление единицы

(A_2–10)^ДК = 1 1000 0001 0111 (B_2–10)^ДК = 0 1001 0010 0100

(B _2–10)^ДК = + 0 1001 0010 0100 Сложение

(A_2–10 + B _2–10)^ДК=10 0001 0011 1011 При суммировании возник

коррекция + 0110 0110 перенос из первой тетрады

(A_2–10 + B _2–10)^ДК= 0 0111 0100 0001 и образовалась запрещенная

(A +B) _2–10 = + 0111 0100 0001 комбинация последней тетраде

(A +B) ₁₀ = + 741

Варианты индивидуальных заданий. Индивидуальное задание студенту определяется преподавателем. В индивидуальном задании требуется произвести операций над числами с ФТ, ПТ и Двоично-десятичном коде.

Вариант к заданию 1

А0	11	− 9	−2	−12	−11	9	8	−4	8
В0	−7	3	−9	−6	5	7	−3	16	−4

Вариант к заданию 2

А0	-145/8	125/8	1105/8	115/8	155/8	165/8	195/8	185/8	175/8
В 0	151/4	171/4	111/4	141/4	131/4	161/4	191/4	181/4	121/4

Вариант к заданию 3

А0	-214	217	-172	747	-174	465	-167	-174	165
В0	324	-171	815	-123	658	-387	917	887	-768

Контрольные вопросы

1. Какие элементы формата чисел с ПТ вы знаете?

2. Чем отличается нормализованное число с ПТ от

ненормализованного числа?

3. Для чего применяются двоично-десятичные коды?

4. Как зависит разрядность чисел от величины основания системы счисления?

5. Можно ли различить форматы целых и дробных чисел с ФТ?

6. Для чего используются машинные коды чисел?

7. Чем отличаются дополнительный и обратный коды отрицательных чисел?

8. Как из ДК отрицательного числа получить ПК числа?

Лабораторная работа 2

Исследование логических основ цифровых автоматов.

Цель работы: Построить логическую схему на основе высказываний путем упрощения выражен

Теоретическая часть:

Теоретической основой построения ЭВМ являются специальные математические дисциплины. Одной из них является алгебра логики, или булева алгебра (Дж. Буль — английский математик прошлого столетия, основоположник этой дисциплины). Ее аппарат широко используют для описания схем ЭВМ, их оптимизации и проектиро­вания.

Вся информация в ЭВМ представляется в двоичной системе счисле­ния. Поставим в соответствие входным сигналам отдельных устройств ЭВМ значения переменных х_i(i = 1, n), а выходным сигналам — значе­ния функций y_j(j=1,m)(рис. 2.1).

Рис. 2.1. Представление схемы ЭВМ

В этом случае зависимостями

где: х_i, — i-йвход;

п — число входов;

у_j—j-й выход;

т — число выходов в устройстве,

можно описывать алгоритм работы любого устройства ЭВМ. Каж­дая такая зависимость у_jявляется «булевой функцией, у которой чис­ло возможных состоянии и каждой ее независимой переменной равно двум» (стандарт ISO 2382/2-76), т.е. функцией алгебры логики, а ее аргументы определены на множестве {0,1}. Алгебра логики устанав­ливает основные законы формирования и преобразования логических функций. Она позволяет представить любую сложную функцию в виде композиции простейших функций. Рассмотрим наиболее употреби­тельные из них.

Известно, что количество всевозможных функций N от п аргу­ментов выражается зависимостью

(2.3)

При n=0 можно определить две основные функции (N=2), не зави­сящие от каких-либо переменных: у₀, тождественно равную нулю (у₀≡0), и у₁тождественно равную единице (y₁≡1). Технической интер­претацией функции y₁≡1 может быть генератор импульсов. При от­сутствии входных сигналов на выходе этого устройства всегда име­ются импульсы (единицы). Функция может быть интерпретиро­вана отключенной схемой, сигналы от которой не поступают ни к каким устройствам.

При п=1 зависимость (2.3) дает N=4. Представим зависимость зна­чений этих функций от значения аргумента х в виде специальной таб­лицы истинности (табл. 2.4).

Таблица 2.4. Таблица функций от одной переменной

Таблицы истинности получили такое название, потому что они определяют значение функции в зависимости от комбинации вход­ных сигналов. В этой таблице, как и ранее, у₀≡0 и y₁≡1. Функция у₂=х, а функция у₃=x (инверсия х).

Этим функциям соответствуют определенные технические анало­ги. Схема, реализующая зависимость у₂₌х,называется повторите­лем, а схема у₃=x— инвертором.

При п=2, N=16, т.е. от двух переменных можно построить шест­надцать различных функций. В табл. 2.5 представлена часть из них, имеющая фундаментальное значение при построении основных схем ЭВМ.

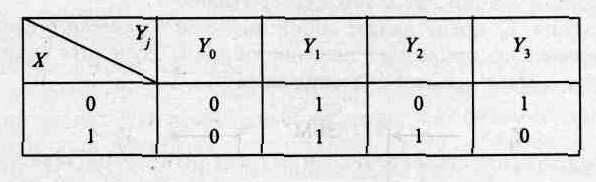
Таблица 2.5 Таблица функций от двух переменных

Заметим, что в левой части таблицы перечислены всевозможные комбинации входных переменных (наборы значений), а в правой — возможные реакции выходных сигналов. В табл. 2.5 представлены функции у₀-у₃, полностью соответствующие функциям из табл. 2.4, а также новые, часто используемые и интересные функции у₄-у₉. При этом местоположение функций и их нумерация в таблице особого зна­чения не имеют. По данной таблице нетрудно составить аналитичес­кое выражение (зависимость) для каждой функции от двух аргумен­тов вида (2.2). Для этого наборы переменных, на которых функция принимает значение единицы, записываются как конъюнкции (логи­ческое умножение) и связываются знаками логического сложения. Такие формы функций получили название дизъюнктивных нормаль­ных форм (ДНФ). Если в этих функциях конъюнкции содержат все без исключения переменные в прямом или инверсном значении, то та­кая форма функций называется совершенной.

Функция y₄ представляет собой функцию логического сложения, дизъюнкцию. Она принимает значение единицы, если хотя бы одна пе­ременная х_{или х₂имеет значение единицы:

Тождественность перечисленных аналитических зависимостей можно установить, пользуясь приведенными ниже законами алгебры логики.

Функция у, является инверсной функцией по отношению к у₄:

Она имеет название «отрицание дизъюнкции». Иногда в литера­туре встречается ее специальное название — «стрелка Пирса», по фа­милии математика, исследовавшего ее свойства.

Функция у₆является функцией логического умножения. Она очень похожа на операцию обычного умножения и принимает значение еди­ницы в тех случаях, когда все ее переменные равны единице:

У₆ = х₁●х₂.

Функция у₇ является инверсной функцией по отношению к у₆:

Она называется «отрицание конъюнкции» или «штрих Шеффера».

Функция y₈ называется логической равнозначностью. Она прини­мает значение единицы, если все ее переменные имеют одинаковое значение (или 0, или 1):

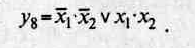
Функция у₉является инверсной функцией по отношению к у₈

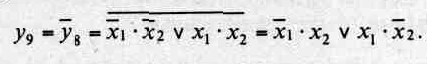
Она принимает значение единицы, если ее переменные имеют про­тивоположные значения. Далее будет показано, что функции у₈и у₉являются основой для построения сумматоров, так как они соответ­ствуют правилам формирования цифр двоичных чисел при сложении (вычитании).

Из перечисленных функций двух переменных можно строить сколь угодно сложные зависимости, отражающие алгоритмы преобразова­ния информации, представленной в двоичной системе счисления. Ал­гебра логики устанавливает правила формирования логически пол­ного базиса простейших функций, из которых могут строиться лю­бые более сложные. Наиболее привычным базисом является набор трех функций {инверсия —｢, дизъюнкция —V, конъюнкция — Λ или &}. Работа с функциями, представленными в этом базисе, очень похожа на использование операций обычной алгебры.

Алгебра логики устанавливает, что существуют и другие комби­нации простейших логических функций, обладающих свойством ло­гической полноты. Например, наборы логических функций {инверсия, дизъюнкция} и (инверсия, конъюнкция} также являются логически полными. Наиболее интересны минимальные базисы, включающие по одной операции {«отрицание дизъюнкции ()»} и {«отрицание конъ­юнкции ()»}- Однако работа с функциями, представленными в ука­занных базисах, требует от специалистов по проектированию ЭВМ определенных навыков.