Национальный минерально-сырьевой университет (Горный)

Отчёт по лабораторной работе №3 По дисциплине: общая и техническая физика.

^{(наименование учебной дисциплины согласно учебному плану)}

Тема: «Изучение магнитного поля. Закон Био-Савара-Лапласа».

Выполнил: студент гр. ЭРБ-12 /Батырев О.Е./

^{(подпись) (Ф.И.О.)}

Принял: профессор / Мартынов В.Л./

^{(подпись) (Ф.И.О.)}

Санкт-Петербург

2013 год.

Цель работы. Измерение магнитных полей, создаваемых проводниками различных конфигураций. Экспериментальная проверка закона Био–Савара–Лапласа.

1. Магнитное поле прямолинейного проводника с током.

П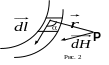 роводник, по которому протекает электрический ток, создает магнитное поле. Магнитное поле характеризуется вектором напряженности H (рис.2), который можно вычислить по формуле H = dH.

Согласно закону Био-Савара-Лапласа,

,

где I – сила тока в проводнике, dl – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.

Индукция магнитного поля рассчитывается по формуле:

,

где ₀ – магнитная постоянная,  – магнитная проницаемость среды (для воздуха  =1)

2. Магнитное поле на оси короткой катушки с током.

Проводник, по которому протекает электрический ток, создает магнитное поле которое характеризуется вектором напряженности H. Напряженность магнитного поля подчиняется принципу суперпозиции

а, согласно закону Био-Савара-Лапласа,

,

где I – сила тока в проводнике, dl – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.

Короткая катушка – цилиндрическая проволочная катушка, состоящая из N витков одинакового радиуса. Из-за осевой симметрии и в соответствии с принципом суперпозиции магнитное поле такой катушки на оси H представляет собой алгебраическую сумму полей отдельных витков H_i: . Таким образом, магнитное поле короткой катушки, содержащей N_к витков, в произвольной точке оси рассчитывается по формулам

, ,

где H – напряженность, B – индукция магнитного поля.

3. Магнитное поле соленоида с током.

Для расчета индукции магнитного поля в соленоиде используется теорема о циркуляции вектора магнитной индукции:

,

где – алгебраическая сумма токов, охватываемых контуром L произвольной формы, n – число проводников с токами, охватываемых контуром. При этом каждый ток учитывается столько раз, сколько раз он охватывается контуром, а положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему, – элемент контура L.

Таким образом, индукция магнитного поля, создаваемого током внутри соленоида вычисляется по формуле: .

Схема установки:

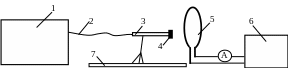
8

1 – измеритель индукции магнитного поля (тесламетр), А – амперметр, 2 – соединительный провод, 3 – измерительный щуп, 4 – датчик Холла, 5 – исследуемый объект (короткая катушка, прямой проводник, соленоид), 6 – источник тока, 7 – линейка для фиксирования положения датчика, 8 – держатель щупа.

Обработка результатов.