
- •Лабораторная работа № 1 решение балансовых моделей на примере межотраслевого баланса
- •1 Теоретические основы
- •1.1 Общая структура межотраслевого баланса
- •1.2 Статическая межотраслевая модель
- •2 Примеры решения задач
- •Лабораторная работа № 2 корреляционно-регрессионный анализ
- •1 Теоретические основы
- •2 Примеры решения задач
2 Примеры решения задач
Задача 1. Имеются данные по 20 сельскохозяйственным хозяйствам. Найти коэффициент корреляции между величинами урожайности зерновых культур и качеством земли и оценить его значимость. Построить уравнение регрессии (линейную модель), которое характеризует прямолинейную зависимость между качеством земли и урожайностью. Выполнить проверку адекватности полученной модели.
Данные приведены в таблице.
Таблица 2.1 - Зависимость урожайности зерновых культур от качества земли
Номер хозяйства |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Качество земли, балл |
32 |
33 |
35 |
37 |
38 |
39 |
40 |
41 |
42 |
44 |
Урожайность, ц/га |
19,5 |
19 |
20,5 |
21 |
20,8 |
21,4 |
23 |
23,3 |
24 |
24,5 |
Продолжение таблицы
Номер хозяйства |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Качество земли, балл |
45 |
46 |
47 |
49 |
50 |
52 |
54 |
55 |
58 |
60 |
Урожайность, ц/га |
24,2 |
25 |
27 |
26,8 |
27,2 |
28 |
30 |
30,2 |
32 |
33 |
Решение
1) Проведем корреляционный анализ.
- Найдем коэффициент парной корреляции. Для нахождения коэффициента корреляции воспользуемся функцией КОРРЕЛ().
Для рассматриваемого примера r=0,9915, n=20.
- Проверим значимость коэффициента корреляции. Значимость коэффициента корреляции проверяется по критерию Стьюдента. Для этого необходимо рассчитать значение t-статистики по формуле
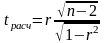

Найдем критическое
значение критерия Стьюдента,
воспользовавшись функцией СТЬЮДРАСПОБР()
со следующими аргументам: Вероятность
– 0,05, Степени свободы – (20-2).
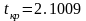 .
.
Сравнив расчетное значение t-статистики с критическим делаем выводы о значимости коэффициента парной корреляции. Если расчетное значение t-статистики больше квантиля распределения Стьюдента, то величина коэффициента корреляции является значимой.
Т.к.
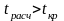 коэффициент корреляции значим.
коэффициент корреляции значим.
2) Проведем регрессионный анализ.
Первый способ. Определение коэффициентов модели и показателей для выполнения проверки адекватности модели.
1. На листе Excel выделить массив свободных ячеек из пяти строк и двух столбцов.
2. Вызвать функцию ЛИНЕЙН.
3.Указать для функции следующие аргументы: Изв_знач_y- столбец значений показателя Урожайность, ц/га; Изв_знач_x- столбец значений показателя Качество земли, балл; Константа –1, Стат– 1 (позволяет вычислить показатели, используемые для проверки адекватности модели. Если Стат– 0, то такие показатели вычисляться не будут).
4. Нажать комбинацию клавиш Ctrl-Shift-Enter.
В выделенные ячейки выводятся коэффициенты модели, а также показатели, позволяющие проверить модель на адекватность (таблица 2).
Таблица 2.2 - Показатели модели
a1= 0,5014 |
a0= 2,5326 |
Se1= 0,0155 |
Se0= 0,7075 |
R2= 0,9830 |
Se= 0,5561 |
F= 1042,5064 |
n-k-1=18,0000 |
QR= 322,4250 |
Qe= 5,5670 |
a1 |
коэффициенты модели |
a0 |
|
Se0 |
стандартные ошибки коэффициентов. Чем точнее модель, тем меньше эти величины |
Se1 |
|
Se |
|
R2 |
коэффициент детерминации. Чем он больше, тем точнее модель |
F |
статистика для проверки значимости модели |
n-k-1 |
число степеней свободы (n-объем выборки, k- количество входных переменных; в данном примере n=20, к=1) |
QR |
сумма квадратов, обусловленная регрессией |
Qe |
сумма квадратов ошибок |
Таким образом, получена следующая модель:
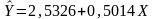
5.
Для проверки адекватности используется
критерий Фишера. Расчетное значение
приведено в Показателях модели. Определим
критическое значение критерия Фишера
Ff.
с помощью функции FРАСПОБР().
Для этого в любой свободной ячейке
ввести функцию FРАСПОБР()
со следующими аргументами: Вероятность
– 0,05, Степени_свободы_1–1,
Степени_свободы_2–18.
Если F>
Ff,
то модель адекватна исходным данным.
Сравнить полученные значения и сделать
выводы.

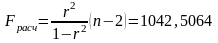
Т.к.
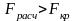 ,
то модель адекватная исходным данным.
,
то модель адекватная исходным данным.
6.
Проверить адекватность построенной
модели можно, используя расчетный
уровень значимости (P).
Ввести функцию FРАСП()
со следующими аргументами: X–
значение статистики F,
Степени_свободы_1
–1,
Степени_свободы_2
– 18. Если
расчетный уровень значимости
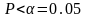 ,
то модель адекватна исходным данным.
Сравнить полученные значения и сделать
выводы.
,
то модель адекватна исходным данным.
Сравнить полученные значения и сделать
выводы.
Т.к.
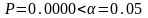 ,
то модель адекватна исходным данным.
,
то модель адекватна исходным данным.
Второй способ. Определение коэффициентов модели с получением показателей для проверки ее адекватности и значимости коэффициентов. ИСХОДНЫЕ ДАННЫЕ ДОЛЖНЫ БЫТЬ ПРЕДСТАВЛЕНЫ В ВИДЕ СТОЛБЦОВ.
Выбрать команду Сервис/Анализ данных/Регрессия.
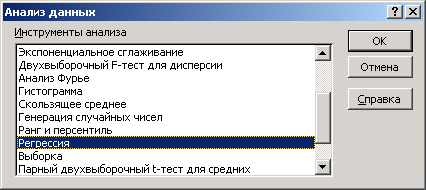
Диалоговое окно Регрессии заполняется следующим образом:

Входной
интервал
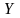 – диапазон (столбец), содержащий данные
со значениями объясняемой переменной;
– диапазон (столбец), содержащий данные
со значениями объясняемой переменной;
Входной
интервал
 – диапазон (столбцы), содержащий данные
со значениями объясняющих переменных.
– диапазон (столбцы), содержащий данные
со значениями объясняющих переменных.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист – можно задать произвольное имя нового листа, в котором будет сохранен отчет.
Если
необходимо получить значения и графики
остатков (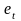 ),
установите соответствующие флажки в
диалоговом окне. Нажмите на кнопку OK.
),
установите соответствующие флажки в
диалоговом окне. Нажмите на кнопку OK.
В диалоговом окне установить: Входной интервал Y – значения показателя Урожайность, ц/га, Входной интервал X – значения показателя Качество земли, балл.
Установить флажок Метки. В области Параметры вывода выбрать переключатель Выходной интервал и указать ячейку, с которой будет начинаться вывод результатов. Для получения результатов нажать кнопку ОК.
Вид отчета о результатах регрессионного анализа представлен на рисунке.
Множественный
R – это
 - коэффициент корреляции, где
- коэффициент корреляции, где
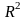 –
коэффициент
детерминации.
Чем ближе его величина к 1, тем более
тесная связь между изучаемыми показателями.
Если знак перед коэффициентом «плюс»,
то связь прямая, если «минус» – обратная.
Для данного примера R=
0,99. Это позволяет сделать вывод, что
качество земли – один из основных
факторов, от которого зависит урожайность
зерновых культур.
–
коэффициент
детерминации.
Чем ближе его величина к 1, тем более
тесная связь между изучаемыми показателями.
Если знак перед коэффициентом «плюс»,
то связь прямая, если «минус» – обратная.
Для данного примера R=
0,99. Это позволяет сделать вывод, что
качество земли – один из основных
факторов, от которого зависит урожайность
зерновых культур.

R-квадрат
- это
.
Коэффициент
является одной из наиболее эффективных
оценок адекватности регрессионной
модели, мерой качества уравнения
регрессии (или, как говорят, мерой
качества подгонки регрессионной модели
к наблюденным значениям
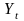 )
)
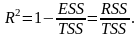
Величина
показывает, какая часть (доля) вариации
объясняемой переменной обусловлена
вариацией объясняющей переменной (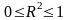 ).
Чем ближе
к единице, тем лучше регрессия
аппроксимирует эмпирические данные.
Если
).
Чем ближе
к единице, тем лучше регрессия
аппроксимирует эмпирические данные.
Если
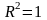 ,
то между
и
существует линейная функциональная
зависимость. Если
,
то между
и
существует линейная функциональная
зависимость. Если
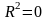 ,
то объясняемая переменная не зависит
от данного набора объясняющих переменных.
Для данного примера показывает, что
урожайность зерновых культур на 98%
зависит от качества почвы, а на долю
других факторов приходится 0,02%.
,
то объясняемая переменная не зависит
от данного набора объясняющих переменных.
Для данного примера показывает, что
урожайность зерновых культур на 98%
зависит от качества почвы, а на долю
других факторов приходится 0,02%.
Нормированный R-квадрат – скорректированный (адаптированный, поправленный(adjusted)) коэффициент детерминации.
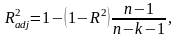
где
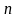 – число наблюдений,
– число наблюдений,
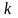 – число объясняющих переменных.
– число объясняющих переменных.
Недостатком
коэффициента детерминации
является то, что он увеличивается при
добавлении новых объясняющих переменных,
хотя это и не обязательно означает
улучшение качества регрессионной
модели. В этом смысле предпочтительнее
использовать
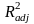 .
В отличие от
скорректированный коэффициент
может уменьшаться при введении в модель
новых объясняющих переменных, не
оказывающих существенное влияние на
зависимую переменную.
.
В отличие от
скорректированный коэффициент
может уменьшаться при введении в модель
новых объясняющих переменных, не
оказывающих существенное влияние на
зависимую переменную.
Стандартная
ошибка
регрессии
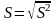 ,
где
,
где
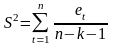 – необъясненная дисперсия (мера разброса
зависимой переменной вокруг линии
регрессии).
– необъясненная дисперсия (мера разброса
зависимой переменной вокруг линии
регрессии).
Наблюдения – число наблюдений.
Отчет приведен в таблице 2.3.
Таблица 2.3а.
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
|
|
|
|
0,0000 |
Остаток |
|
|
|
|
|
Итого |
|
|
|
|
|
Таблица 2.3б.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Y-пересечение |
|
|
|
0,0021 |
1,0462 |
4,0189 |
Качество земли, балл |
|
|
|
0,0000 |
0,4688 |
0,5340 |
Таким образом, получена следующая модель:
Интерпретация коэффициентов модели. В данном примере с увеличением качества почвы на один балл, урожайность зерновых культур повышается в среднем на 0,5014 ц/га.
df
– degrees of freedom – число степеней свободы
связано с числом единиц совокупности
и с числом определяемых по ней констант
 .
.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
По эмпирическому значению статистики F проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F-статистика больше эмпирического значения F.
Уравнение
регрессии значимо на уровне
,
если
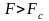 ,
где
,
где
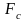 - табличное значение F-критерия
Фишера (
- табличное значение F-критерия
Фишера (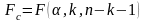 ).
).
На
уровне значимости
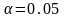 гипотеза
гипотеза
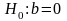 отвергается, если Значимость
отвергается, если Значимость
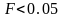 ,
и принимается, если Значимость
,
и принимается, если Значимость
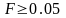 .
.
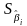 –
стандартные ошибки
коэффициентов.
–
стандартные ошибки
коэффициентов.
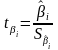 – t-статистика
соответствующего коэффициента
– t-статистика
соответствующего коэффициента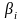 .
.
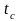 –
критическая точка
распределения Стьюдента,
–
критическая точка
распределения Стьюдента,
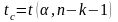 .
.
Если
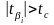 ,
то коэффициент
считается статистически значимым.
,
то коэффициент
считается статистически значимым.
Если
 ,
то коэффициент
считается статистически незначимым.
Это означает, что фактор
,
то коэффициент
считается статистически незначимым.
Это означает, что фактор
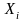 линейно не связан с зависимой переменной
.
Его наличие среди объясняющих переменных
не оправдано со статистической точки
зрения. Поэтому после установления того
факта, что коэффициент
незначим, рекомендуется исключить из
уравнения регрессии переменную
.
Это не приведет к существенной потере
качества модели, но сделает ее более
корректной.
линейно не связан с зависимой переменной
.
Его наличие среди объясняющих переменных
не оправдано со статистической точки
зрения. Поэтому после установления того
факта, что коэффициент
незначим, рекомендуется исключить из
уравнения регрессии переменную
.
Это не приведет к существенной потере
качества модели, но сделает ее более
корректной.
Проверка статистической значимости коэффициентов модели выполняется по расчетным уровням значимости P, указанным в столбце P-значение. P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии .
Для уровня значимости :
Если
P-Значение
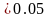 ,
то коэффициент
незначим, следовательно, гипотеза
,
то коэффициент
незначим, следовательно, гипотеза
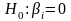 принимается.
принимается.
Если P-Значение , то коэффициент значим, следовательно, гипотеза отвергается.
Нижние 95% - Верхние 95% - доверительный интервал для параметра .
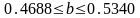 ,
т.е. с надежностью 0.95 этот коэффициент
лежит в данном интервале. Поскольку
коэффициент регрессии в эконометрических
исследованиях имеют четкую экономическую
интерпретацию, то границы доверительного
интервала для коэффициента регрессии
не должны содержать противоречивых
результатов, например,
,
т.е. с надежностью 0.95 этот коэффициент
лежит в данном интервале. Поскольку
коэффициент регрессии в эконометрических
исследованиях имеют четкую экономическую
интерпретацию, то границы доверительного
интервала для коэффициента регрессии
не должны содержать противоречивых
результатов, например,
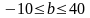 .
Такого рода запись указывает, что
истинное значение коэффициента регрессии
одновременно содержит положительные
и отрицательные величины и даже ноль,
чего не может быть.
.
Такого рода запись указывает, что
истинное значение коэффициента регрессии
одновременно содержит положительные
и отрицательные величины и даже ноль,
чего не может быть.
Третий способ. ГРАФИЧЕСКИЙ СПОСОБ ПОСТРОЕНИЯ МОДЕЛИ.
Самостоятельно построить точечную диаграмму, отражающую связь между урожайностью и качеством земли.
Получить линейную модель зависимости урожайности зерновых культур от качества земли. Для этого выделив построенный ряд зависимости, нажать на правую клавишу мышки и в контекстном меню выбрать команду Добавить линию тренда. В появившемся окне выбираем вид модели и добавляем на график уравнение тренда и коэффициент детерминации (величина достоверности аппроксимации).
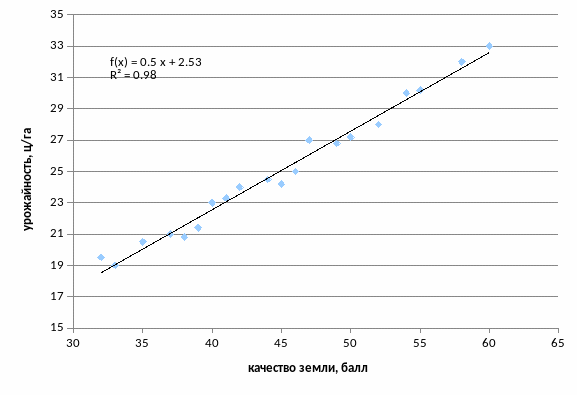
Построить самостоятельно полиномиальную модель регрессии второго порядка.

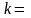 1
1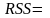 322,425
322,425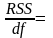 322,4250
322,4250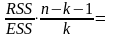 1042,5064
1042,5064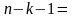 18
18 5,5670
5,5670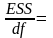 0,3093
0,3093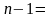 19
19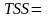 327,9920
327,9920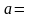 2,5326
2,5326 0,7075
0,7075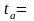 3,5797
3,5797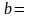 0,5014
0,5014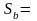 0,0155
0,0155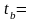 32,2879
32,2879