Лабораторная работа № 2 корреляционно-регрессионный анализ

1 Теоретические основы

Корреляционная связь - это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений.

Парная корреляция - это связь между двумя показателями, один из которых является факторным, а другой - результативным.

Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.

Необходимые условия применения корреляционного анализа:

1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей.

2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

Применение корреляционного анализа позволяет решить следующие задачи:

1.Определить изменение результативного показателя под воздействием одного или нескольких факторов.

2. Установить относительную степень зависимости результативного показателя от каждого фактора.

Линейная регрессия сводится к нахождению уравнения вида

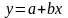или .

Уравнение вида позволяет по заданным значениям фактора х иметь теоретические значения результативного признака, подставляя в него фактические значения факторах На графике теоретические значения представляют линию регрессии (рисунок 1.2).

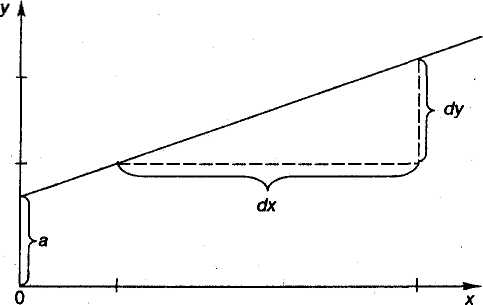
Рисунок 1.2 - Графическая оценка параметров линейной регрессии

Построение линейной регрессии сводится к оценке ее параметров — а и b. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию. Далее по графику можно определить значения параметров.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) 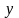минимальна:

.

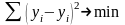Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рисунок 1.3):

,

следовательно, чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю.

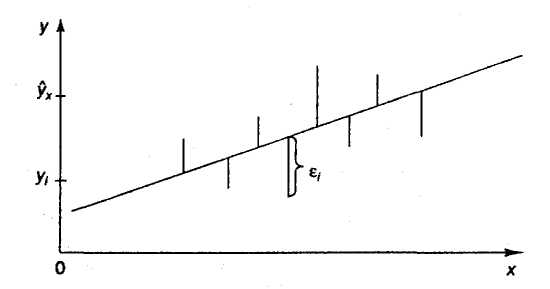
Рисунок 1.3 - Линия регрессии с минимальной дисперсией остатков

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Формально а — значение у при х = 0. Если признак-фактор х не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Попытки экономически интерпретировать параметр а могут привести к абсурду, особенно при а < 0.

Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация результата меньше вариации фактора — коэффициент вариации по фактору х выше коэффициента вариации для результата у.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции. Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и, следовательно, фактор х не оказывает влияния на результат у.

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: т_b и т_a.

Стандартная ошибка коэффициента регрессии определяется по формуле

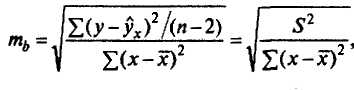
где S² — остаточная дисперсия на одну степень свободы.

Величина стандартной ошибки совместно с t-распределением Стьюдента при n-2 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительных интервалов.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдента: , которое затем сравнивается с табличным значением при определенном уровне значимости 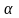и числе степеней свободы (n-2).

Стандартная ошибка параметра а определяется по формуле:

Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется t-критерий: 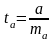, его величина сравнивается с табличным значением при df=n-2 степенях свободы.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции :

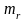Фактическое значение t-критерия Стьюдента определяется как

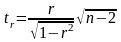
Данная формула свидетельствует, что в парной линейной регрессии , ибо, как уже указывалось, . Кроме того, 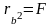. Следовательно, .

Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

Для проведения регрессионного анализа и прогнозирования необходимо:

1. построить график исходных данных и попытаться зрительно, приближенно определить характер зависимости;

2. выбрать вид функции регрессии, которая может описывать связь исходных данных (в нашем случае линейная);

3. определить численные коэффициенты функции регрессии;

4. оценить силу найденной регрессионной зависимости на основе коэффициента детерминации ;

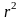5. сделать прогноз (при 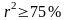) или сделать вывод о невозможности прогнозирования с помощью найденной регрессионной зависимости. При этом не рекомендуется использовать модель регрессии для тех значений независимого параметра X, которые не принадлежат интервалу, заданному в исходных данных.