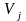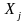- •Лабораторная работа № 1 решение балансовых моделей на примере межотраслевого баланса
- •1 Теоретические основы
- •1.1 Общая структура межотраслевого баланса
- •1.2 Статическая межотраслевая модель
- •2 Примеры решения задач
- •Лабораторная работа № 2 корреляционно-регрессионный анализ
- •1 Теоретические основы
- •2 Примеры решения задач
2 Примеры решения задач
Задача 1. Для трехотраслевой экономической системы заданы:
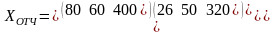 - промежуточный продукт,
- промежуточный продукт,
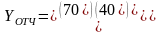 - вектор конечной
продукции,
- вектор конечной
продукции,
 - валовой выпуск
продукции в плановом периоде,
- валовой выпуск
продукции в плановом периоде,
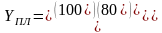 - вектор конечной
продукции в плановом периоде.
- вектор конечной
продукции в плановом периоде.
Задание:
составить схему отчетного межотраслевого баланса;
рассчитать плановый межотраслевой баланс при условии, что в плановый период известен валовой выпуск продукции;
найти вектор валового выпуска продукции в плановый период при известном конечном использовании.
Решение. Для решения задачи используем процессор Excel.
1 Схема межотраслевого баланса
Отрасли производители |
Отрасли потребители |
Промежуточное потребление, |
Конечное использование,
|
Валовой выпуск,
|
||
1 |
2 |
3 |
||||
1 |
80 |
60 |
400 |
|
|
|
2 |
26 |
50 |
320 |
|
|
|
3 |
40 |
70 |
240 |
|
|
|
Промежуточные затраты, |
|
|
|
|
|
|
Валовая добавленная стоимость,
|
|
|
|
|
|
|
Валовой выпуск,
|
|
|
|
|
|
|
Промежуточное
потребление равно
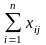 .
Для первой отрасли 80+60+400=540, для второй
26+50+320=396, для третьей 40+70+240=350.
.
Для первой отрасли 80+60+400=540, для второй
26+50+320=396, для третьей 40+70+240=350.
Валовой выпуск равен . Для первой отрасли 70+540=610, для второй 40+396=436, для третьей 50+350=400.
Промежуточные
затраты равны
 .
Для первой отрасли 80+26+40=146, для второй
60+50+70=180, для третьей 400+320+240=960.
.
Для первой отрасли 80+26+40=146, для второй
60+50+70=180, для третьей 400+320+240=960.
Валовая
добавленная стоимость равна
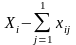 .
Для первой отрасли 610-146=464, для второй
436-180=256, для третьей 400-960=-560.
.
Для первой отрасли 610-146=464, для второй
436-180=256, для третьей 400-960=-560.
Схема фактического межотраслевого баланса
Отрасли производители |
Отрасли потребители |
Промежуточное потребление, |
Конечное использование, |
Валовой выпуск, |
||
1 |
2 |
3 |
||||
1 |
80 |
60 |
400 |
540 |
70 |
610 |
2 |
26 |
50 |
320 |
396 |
40 |
436 |
3 |
40 |
70 |
240 |
350 |
50 |
400 |
Промежуточные затраты, |
146 |
180 |
960 |
1286 |
160 |
1446 |
Валовая добавленная стоимость, |
464 |
256 |
-560 |
160 |
|
|
Валовой выпуск, |
610 |
436 |
400 |
1446 |
|
|
2 Рассчитать плановый межотраслевой баланс при условии, что в плановый период известен валовой выпуск продукции.
Рассчитаем
коэффициенты прямых затрат
 .
.
Матрица прямых затрат (А) имеет следующий вид:
0,13115 |
0,13761 |
1,00000 |
0,04262 |
0,11468 |
0,80000 |
0,06557 |
0,16055 |
0,60000 |
Матрица «Затраты - Выпуск» равна В = Е – А.
0,86885 |
-0,13761 |
-1,00000 |
-0,04262 |
0,88532 |
-0,80000 |
-0,06557 |
-0,16055 |
0,40000 |
Вектор
конечного использования равен произведению
матрицы В на ХПЛ
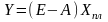 (можно воспользоваться функцией МУМНОЖ
()).
(можно воспользоваться функцией МУМНОЖ
()).
-863,385 |
-569,488 |
343,537 |
Полученные значения не допустимы, т. к. объем конечного потребления – это положительная величина. В данном случае отрицательное значение объясняется тем, что промежуточное потребление по отраслям 1 и 2 больше значения ХПЛ.
Объемы межотраслевых поставок определяются по формуле
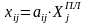 .
.
26,2295 |
37,1560 |
1000,0000 |
8,5246 |
30,9633 |
800,0000 |
13,1148 |
43,3486 |
600,0000 |
Схема баланса на плановый период.
Отрасли производители |
Отрасли потребители |
Промежуточное потребление |
Конечное использование |
Валовой выпуск |
|||||
1 |
2 |
3 |
|||||||
1 |
26,2 |
37,2 |
1000,0 |
1063,4 |
-863,4 |
200,0 |
|||
2 |
8,5 |
31,0 |
800,0 |
839,5 |
-569,5 |
270,0 |
|||
3 |
13,1 |
43,3 |
600,0 |
656,5 |
343,5 |
1000,0 |
|||
Промежуточные затраты |
47,9 |
111,5 |
2400,0 |
2559,3 |
-1089,3 |
1470,0 |
|||
Валовая добавленная стоимость |
152,1 |
158,5 |
-1400,0 |
-1089,3 |
|
|
|||
Валовой выпуск |
200 |
270 |
1000 |
1470,0 |
|
|
|||
3. Найти вектор валового выпуска продукции в плановый период при известном конечном использовании.
Найдем
обратную матрицу к матрице «Затраты-Выпуск»
 (можно использовать функцию =МОБР())
(можно использовать функцию =МОБР())
Вектор валового выпуска продукции в плановый период равен (можно использовать функцию МУМНОЖ ()).
1145,7772 |
849,1406 |
778,6571 |
Задача 2. В экономике работают 3 отрасли, каждая из которых затрачивает на воспроизводство продукции 3 вида ресурса (межотраслевые потоки):
894,6 |
170,0 |
972,7 |
517,0 |
850,0 |
5,0 |
775,3 |
170,0 |
486,3 |
Валовая продукция каждой отрасли представлена в таблице:
Отрасль |
Xi |
1 |
2584,3 |
2 |
1700,3 |
3 |
2432,0 |
Проверить матрицу прямых затрат на продуктивность разными способами.
Решение.
Для того чтобы матрица коэффициентов прямых материальных затрат А была продуктивной, необходимо и достаточно чтобы выполнялось одно из перечисленных ниже условий:
1) матрица (Е - А) неотрицательно обратима, т.е. существует обратная матрица (Е - А)-1 0;
2)
матричный ряд Е+А+
А2
+ А3+...=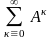
 сходится,
причем его
сумма равна обратной матрице (Е
- А) -1;
сходится,
причем его
сумма равна обратной матрице (Е
- А) -1;
3) все главные миноры матрицы (Е - А), т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы, порядка от 1 до п, положительны;
4) наибольшее по модулю собственное значение Х матрицы А, то есть решение характеристического уравнения Е - А = 0, строго меньше единицы.
Проверим первое
условие.
Исходные данные поместим на рабочий
лист Excel. Вычислим матрицу прямых затрат
А
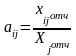 .
Матрица А имеет вид:
.
Матрица А имеет вид:
0,3462 |
0,1000 |
0,4000 |
0,2001 |
0,4999 |
0,0021 |
0,3000 |
0,1000 |
0,2000 |
Строим матрицу Е.
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Вычислим матрицу ЕА:
0,6538 |
-0,1000 |
-0,4000 |
-0,2001 |
0,5001 |
-0,0021 |
-0,3000 |
-0,1000 |
0,8000 |
Строим матрицу В = (ЕА)-1 (можно использовать функцию =МОБР()).Получаем:
2,2543 |
0,6764 |
1,1287 |
0,9057 |
2,2724 |
0,4586 |
0,9585 |
0,5376 |
1,7305 |
Поскольку существует обратная матрица (Е - А)-1, все элементы которой неотрицательны, то данная матрица является продуктивной.
Проверим второе условие. Вычислим элементы матриц A2, A3 и т.д., используя функцию МУМНОЖ().
A2 |
|
|
|
A3 |
|
|
|
A4 |
|
|
0,2598 |
0,1246 |
0,2186 |
|
0,1805 |
0,1101 |
0,1479 |
|
0,1289 |
0,0879 |
0,1020 |
0,1699 |
0,2701 |
0,0815 |
|
0,1373 |
0,1602 |
0,0848 |
|
0,1050 |
0,1023 |
0,0722 |
0,1838 |
0,1000 |
0,1602 |
|
0,1317 |
0,0844 |
0,1058 |
|
0,0942 |
0,0659 |
0,0740 |
Как видим, элементы
матриц уменьшаются, что позволяет
предположить, что матричный ряд Е+А+
А2
+ А3+...=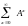 сходится.
Суммируем матрицы Е, А,
А2,
А3,
А4,
А5,
А6
и т.д., т.к. сумма стремиться к (Е
- А)-1,
то матрица является продуктивной.
сходится.
Суммируем матрицы Е, А,
А2,
А3,
А4,
А5,
А6
и т.д., т.к. сумма стремиться к (Е
- А)-1,
то матрица является продуктивной.
Е+А+ А2 |
|
Е+А+ А2 + А3 |
||||||
1,6060 |
0,2246 |
0,6186 |
|
1,7864 |
0,3347 |
0,7665 |
||
0,3699 |
1,7700 |
0,0835 |
|
0,5072 |
1,9302 |
0,1683 |
||
0,4838 |
0,2000 |
1,3601 |
|
0,6155 |
0,2843 |
1,4659 |
||
Е+А+ А2 + А3+ А4 |
|
Е+А+ А2 + А3+ А4+ А5 |
||||||
1,9153 |
0,4226 |
0,8685 |
|
1,9825 |
0,4725 |
0,9201 |
||
0,6122 |
2,0325 |
0,2405 |
|
0,6701 |
2,0804 |
0,2833 |
||
0,7097 |
0,3502 |
1,5399 |
|
0,7590 |
0,3872 |
1,5777 |
||
Е+А+ А2 + А3+ А4+ А5+ А6 |
|
Е+А+ А2 + А3+ А4+ А5+ А6+ А7 |
||||||
2,0083 |
0,4923 |
0,9398 |
|
2,0155 |
0,4979 |
0,9453 |
||
0,6928 |
2,0981 |
0,3005 |
|
0,6992 |
2,1030 |
0,3054 |
||
0,7780 |
0,4017 |
1,5921 |
|
0,7833 |
0,4058 |
1,5962 |
||
….
Проверим третье условие. Вычислим главные миноры матрицы (Е - А).
Главным минором
порядка
![]() квадратной матрицы
квадратной матрицы
![]() называется определитель
называется определитель

т.е. определитель,
образованный первыми
![]() строками и первыми
столбцами матрицы.
строками и первыми
столбцами матрицы.
Для расчета миноров используем функцию МОПРЕД().
Получим:
M1 |
0,6538 |
M2 |
0,3070 |
M3 |
0,1774 |
Как видим, все главные миноры матрицы (Е - А) положительны.