Контрольные вопросы

1. Что является объектом оценки бизнеса?

2. Сформулируйте основные цели оценки стоимости бизнеса.

3. Назовите источники формирования дохода при использовании предприятия с точки зрения оценки стоимости бизнеса.

4. Назовите виды стоимости, отражающие источники образования дохода.

5. Охарактеризуйте оценочные принципы, их преимущества и недостатки.

6. В ходе фундаментального анализа оценщик приходит к заключению о том, что рыночная стоимость акций выше их предполагаемой внутренней стоимости. Какой вывод должен сделать оценщик?

7. Что означает процедура дисконтирования будущих денежных потоков?

8. Какие методы оценки предприятий объединяет:

   • затратный подход;

   • доходный подход;

   • сравнительный подход?

9. По заказу Совета директоров Общества была произведена оценка рыночной стоимости предприятия, которая составила 2 миллиона долларов. Для предприятий данной отрасли рынок предполагает премию за контроль – 25 %, скидку на недостаток ликвидности – 30 %, в том числе скидку, рассчитанную на основе затрат по выходу на открытый рынок для компаний с аналогичным размером капитала – 20 %. Необходимо оценить стоимость 75 %-го и 4 %-го пакета акций данного предприятия (рассмотреть вариант для ЗАО и ОАО).

2 Доходный подход к оценке предприятий

2.1 Стоимость денег во времени. Временная оценка денежных потоков

Принятие решения о вложении капитала определяется, в ко­нечном счете, величиной дохода, который инвестор предполагает получить в будущем. Например, приобретая сейчас облигацию, мы рассчитываем в течение всего срока займа регулярно получать доход в виде начисленных процентов, а по окончании получить основную сумму долга. Вложение капитала выгодно только в том случае, если предполагаемые поступления превысят текущие рас­ходы. В нашем примере инвестиционный доход равен сумме полу­ченных процентов, так как затраты на покупку облигаций будут совпадать с выплатами по принципалу, однако положительные денежные потоки (выплата процентов и основной суммы долга) и отрицательные денежные потоки (инвестирование каптала) не бу­дут совпадать по времени возникновения и, следовательно, будут не сопоставимы.

Теория стоимости денег исходит из предположения, что день­ги, являясь специфическим товаром, со временем меняют свою стоимость и, как правило, обесцениваются. Изменение со временем стоимости денег происходит под влиянием целого ряда факторов.

Важнейшими факторами можно назвать инфляцию и способ­ность денег приносить доход при условии их разумного инвести­рования в альтернативные проекты.

Таким образом, в нашем примере мы должны сравнивать за­траты на приобретение облигации с суммой предстоящих доходов, приведенных по стоимости к моменту инвестирования.

Приведение денежных сумм, возникающих в разное время, к сопоставимому виду называется временной оценкой денежных по­токов. Временная оценка денежных потоков основана на исполь­зовании шести функций сложного процента.

1. Сложный процент.

2. Дисконтирование.

3. Текущая стоимость аннуитета.

4. Периодический взнос в погашение кредита.

5. Будущая стоимость аннуитета.

6. Периодический взнос в фонд накопления.

Теория и практика использования указанных функций слож­ного процента базируется на ряде допущений.

1. Денежный поток – это денежные суммы, возникающие в определенной хронологической последовательности.

2. Денежный поток, в котором все суммы различаются по ве­личине, называется обычным денежным потоком.

3. Денежный поток, в котором все суммы равновеликие, называется аннуитетом.

4. Суммы денежного потока возникают через одинаковые промежутки времени, называемые периодом.

5. Денежный поток может возникать в конце периода, а также в начале и середине периода.

6. Предварительно рассчитанные таблицы сложного процента без корректировки применимы только к денежному потоку, возни­кающему в конце периода.

7. Доход, получаемый на инвестированный капитал, из хозяйственного оборота не изымается, а присоединяется к основному капиталу.

8. Ставка дохода на инвестиции – это процентное соотно­шение между чистым доходом и вложенным капиталом.

Для приведения денежных потоков к сопоставимому виду существуют так называемые множительные таблицы.

Таблицы тип А – систематизированы по видам функций сложного процента. Для их использования необходимо определить используемую функцию и на пересечении строки, соответствую­щей периоду, и столбца, адекватного ставке дисконта, найти мно­житель, позволяющий откорректировать ту или иную сумму.

Таблицы тип В – сгруппированы по величине процентной ставки. Для решения задачи в этом случае необходимо сначала найти страницу, совпадающую со ставкой дисконта, а затем на пе­ресечении столбца, совпадающего с нужной функцией, и строки, соответствующей периоду, найти множитель.

Сложный процент.

Символ функции – FV.

Таблицы тип В – колонка № 1.

Данная функция позволяет определить будущую стоимость суммы, которой располагает инвестор в настоящий момент, исходя из предполагаемой ставки дохода, срока накопления и периодич­ности начисления процентов.

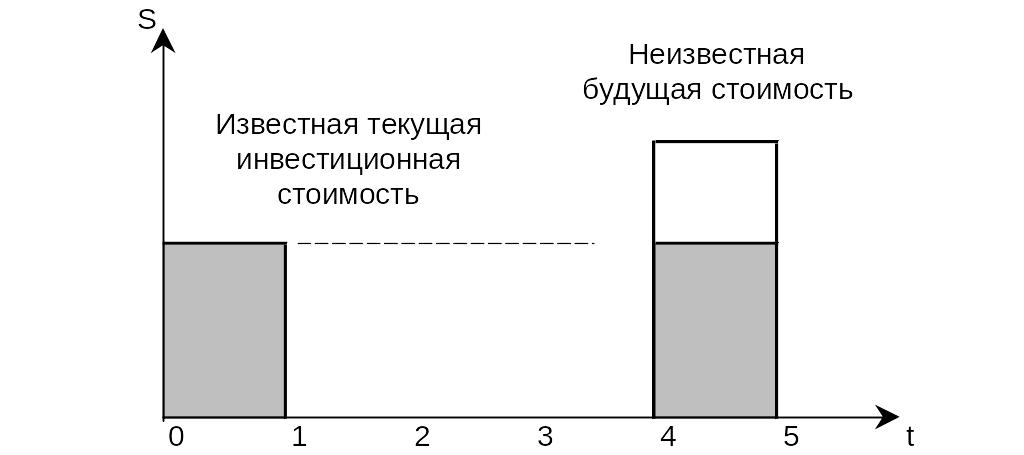
Рис. 1 Возрастание по сложному проценту текущей стоимости,

S – инвестиционная стоимость;

t – время, годы.

Расчет будущей стоимости основан на логике сложного процента, который представляет геометрическую зависимость между первоначальным вкладом, процентной ставкой и периодом накопления.

, где

FV – величина накопления;

S – первоначальный вклад;

i – процентная ставка;

n – число периодов начисления процентов.

Задача, которая, по сути, является алгоритмом, позволяющим решать самые разнообразные инвестиционные вопросы, может быть сформулирована следующим образом.

Какая сумма будет накоплена вкладчиком через три года, если первоначальный взнос составляет 400 тыс. руб., проценты начисляются ежегодно по ставке 10%?

Решение:

1. Найдем страницу, соответствующую процентной ставке – 10%.

2. В колонке № 1 найдем фактор, соответствующий периоду накопления¹.

3. Период накопления – 3, фактор – 1,3310.

4. Рассчитаем сумму накопления

400 х FV^3(10%) = 400 х 1,3310 = 532,4 тыс. руб.

Таким образом, сложный процент предполагает начисление процентов не только на сумму первоначального взноса, но и на сумму процентов, накопленных к концу каждого периода. Это возможно только в случае реинвестирования суммы начисленных процентов, т.е. присоединения их к инвестиционному капиталу.

Техника простого процента предполагает арифметическую зависимость между суммой вклада, процентной ставкой и периодом накопления. Следовательно, простой процент начисляется только один раз в конце срока депозитного договора. Если бы приведен­ная выше ситуация предполагала начисление простого процента, то накопленная сумма составила:

400(1+0,10 х 3) = 520 тыс. руб.

Периодичность начисления процентов оказывает влияние на величину накопления. Чем чаще начисляются проценты, тем больше накопленная сумма. При более частом накоплении необходимо откорректировать процентную ставку и число периодов начисления процентов:

Для определения периода времени, необходимого для удвое­ния первоначального вклада используется правило 72-х. Это пра­вило дает наиболее точные результаты, если процентная ставка находится в интервале 3-18%.

Удвоение первоначального вклада произойдет через число пе­риодов, равное

частному от деления 72 на процентную ставку соответствующего периода.

Дисконтирование.

Символ функции – PV.

Таблицы тип В – колонка № 4.

Функция дисконтирования дает возможность определить настоящую стоимость суммы, если известна ее величина в будущем при данном периоде накопления и процентной ставке. Настоящая стоимость, а также текущая или приведенная стоимости являются синонимичными понятиями.

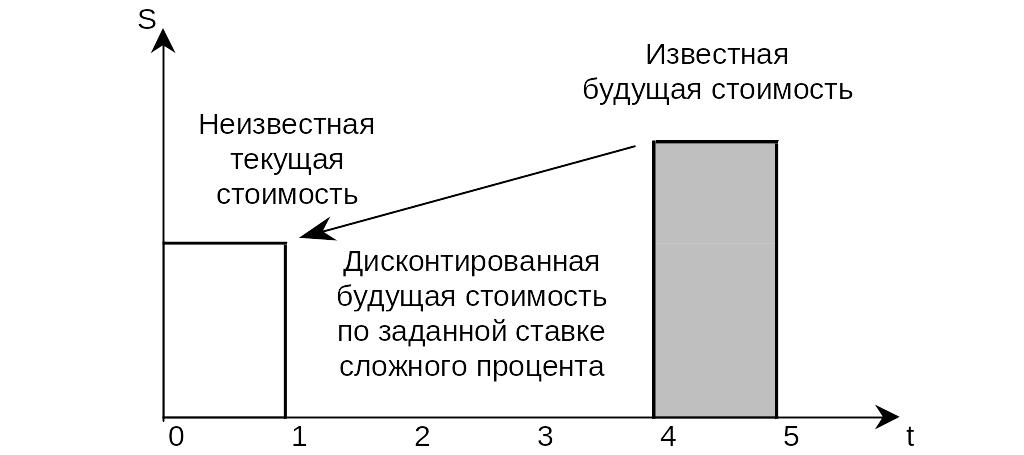
Рис. 2 Текущая стоимость денежной единицы,

S – депозитная сумма;

t – время, годы.

Задача-алгоритм.

Какую сумму необходимо поместить на депозит под 10% го­довых, чтобы через 5 лет накопить 1500 тыс. руб.

Решение:

1. Находим таблицу, соответствующую процентной ставке – 10%.

2. В колонке № 4 найдем фактор, исходя из периода дисконтирования в 5 лет – 0,6209.

3. Рассчитаем сумму вклада

1500 х PV^5(10%) = 1500 х 0,6209 = 931,4 тыс. руб

Таким образом, инвестирование 931,4 тыс. руб. на 5 лет при ставке дохода 10% обеспечит накопление в сумме 1500 тыс. руб. Формула дисконтирования:

, где

PV – текущая стоимость;

S – известная в будущем сумма;

i – процентная ставка;

n – число периодов начисления процентов.

Функция дисконтирования является обратной по отношению к функции сложного процента.

Текущая стоимость аннуитета.

Символ функции – PVA.

Таблицы тип В – колонка № 5.

Аннуитет – это денежный поток, в котором одинаковые по величине суммы возникают через одинаковые промежутки време­ни. Аннуитет может быть исходящим денежным потоком по отно­шению к инвестору (например осуществление периодических рав­ных платежей), либо входящим денежным потоком (например, поступление арендной платы, которая обычно устанавливается одинаковой фиксированной суммой).

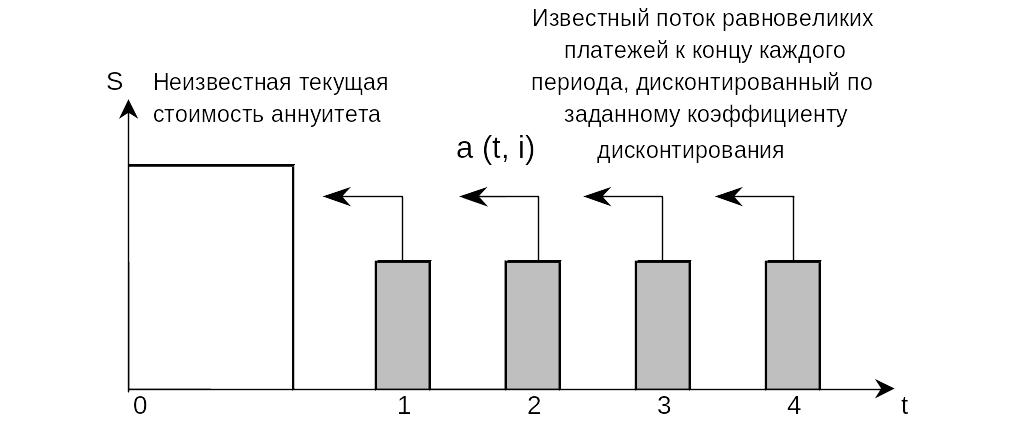
Рис. 3 Текущая стоимость обычного аннуитета,

S – инвестиционная сумма;

t – время, годы.

Задача-алгоритм.

Какую сумму необходимо положить на депозит под 100% го­довых, чтобы затем 5 раз снять по 300 тыс. руб.?

Решение:

1. Находим страницу, соответствующую процентной ставке 10%.

2. Находим фактор текущей стоимости аннуитета в колонке № 5 и строке, соответствующей периоду существования аннуитета – 3,7908.

3. Рассчитаем текущую стоимость аннуитета

300 х PVA^5(10%) = 300 х 3,7908 = 1137 тыс. руб.

Таким образом, инвестор снимает со счета пять раз по 300 тыс. руб. или 1500 тыс. руб. Разница между первоначальным вкладом 1137 тыс. руб. и накоплением – 1500 тыс. руб. обеспе­чивается суммой процентов, которые начисляются на уменьшаю­щийся остаток вклада по технике сложного процента. Этот про­цесс предполагает, в конечном счете, нулевой остаток на депозите.

Предыдущие рассуждения основывались на предположении, что аннуитет возникает в конце периода. Такой аннуитет называ­ется обычным.

Однако на практике возможна ситуация, когда первый платеж произойдет одновременно с начальным поступлением. В после­дующем аннуитеты будут возникать через равные интервалы. Та­кой аннуитет называется авансовым или причитающимся аннуите­том.

Для того чтобы определить текущую стоимость авансового ан­нуитета, необходимо проследить движение денежного потока. По­скольку первый аннуитет по времени совпадает с депонированием основного вклада, его не следует дисконтировать. Все последую­щие аннуитеты дисконтируются в обычном порядке, однако пери­од дисконтирования всегда будет на единицу меньше. Следова­тельно, фактор текущей стоимости авансового аннуитета соответ­ствует фактору обычного аннуитета для предыдущего периода, к которому добавлена единица. Эта добавленная единица обеспечи­вает заданный поток аннуитета.

Периодический взнос на погашение кредита.

Символ функции – PMT.

Таблица тип В — колонка № 6.

Временная оценка денежных потоков может поставить перед аналитиком проблему определения величины самого аннуитета, если известна его текущая стоимость, число взносов и ставка до­хода.

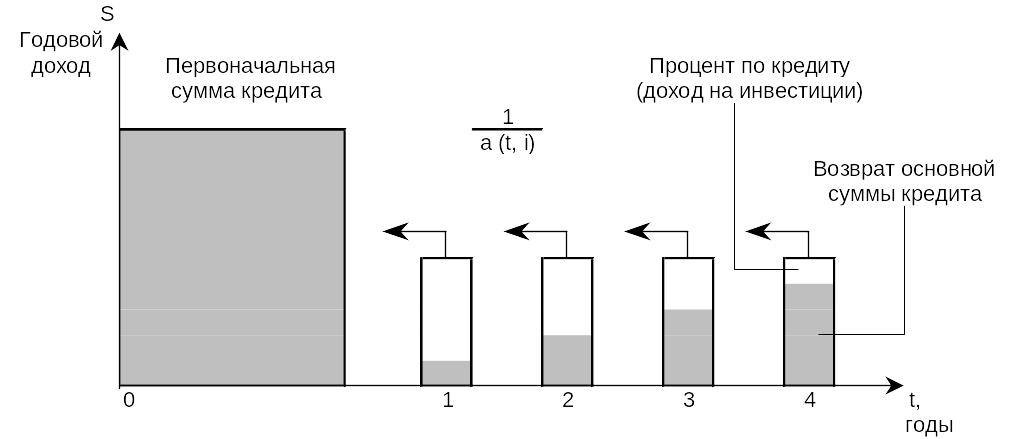
Рис. 4 Периодический взнос на погашение кредита.

Задача-алгоритм.

Какую сумму можно ежегодно снимать со счета в течение пяти лет, если первоначальный вклад равен 1500 тыс. руб., банк на­числяет ежегодно 14% и при условии, что снимаемые суммы будут одинаковы.

Решение:

1. Находим фактор взноса на погашение кредита при условии, что взносов будет 5, а ставка 14% (колонка №6). Фактор ра­вен 0,2913.

2. Рассчитаем величину аннуитета

1500 х PMT^5(14%) = 1500 х 0,2913 = 437 тыс. руб.

Таким образом, если положить на счет под 14% годовых 1500 тыс. руб., можно пять раз в конце года снять по 437 тыс. руб. Дополнительно полученные деньги в сумме (437 х 5)-1500 = 685 тыс. руб. являются результатом начисления процентов на уменьшающийся остаток вклада.

Функция «периодический взнос на погашение кредита» явля­ется обратной по отношению к функции «текущая стоимость ан­нуитета».

Аннуитет по определению может быть как поступлением, (т.е. входящим денежным потоком), так и платежом, (т.е. исходящим денежным потоком) по отношению к инвестору. Поэтому данная функция может использоваться в случае необходимости расчета величины равновеликого взноса в погашении кредита при задан­ном числе взносов и заданной процентной ставке. Такой кредит называют самоамортизирующимся.

Например, рассчитать величину ежегодного взноса в погаше­ние кредита в сумме 40000 тыс. руб., предоставленного на 15 лет под 20% годовых.

Решение:

1. Определим фактор периодического взноса на погашение кредита, если ставка – 20%, а число взносов – 15 (колонка №6) - 0,2139.

2. Рассчитаем величину взноса

40000 х PMT^15(20%) = 40000 х 0,2139 = 8555,3 тыс. руб.

Заемщик уплатил кредитору за 15 лет 128329,3 = (8555,3 х 15) тыс. руб., что превышает величину выданного кредита на 128329,3-40000 = 88329,3 тыс. руб. Разница является суммой процентов, уплаченных заемщиком за весь период кредитования, при условии, что основной долг по­стоянно уменьшается.

Будущая стоимость аннуитета.

Символ функции – FVА.

Таблица тип В – колонка № 2.

Данная функция позволяет рассчитать величину накопленных равновеликих взносов при заданной ставке дохода.

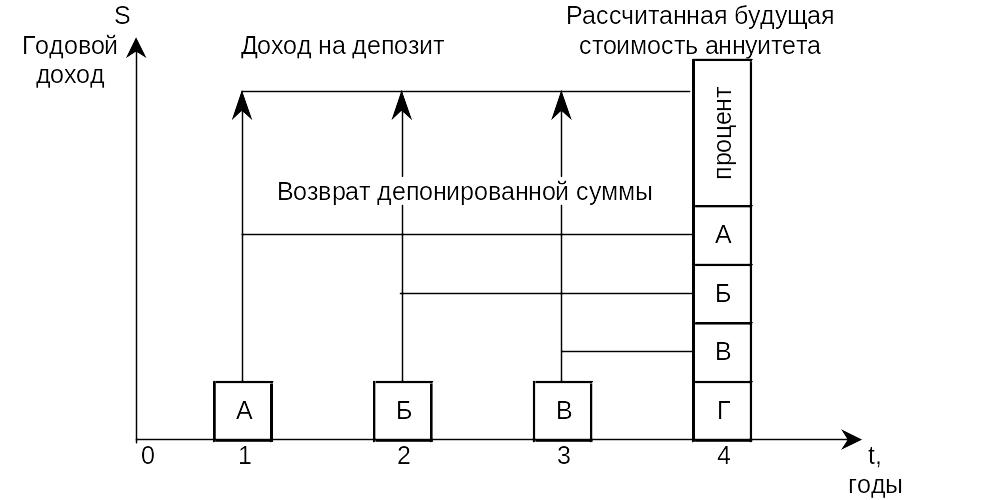
Рис. 5 Накопление единицы за период.

Задача-алгоритм.

Какая сумма будет накоплена на счете, если в течение 4 лет ежегодно вносить 350 тыс. руб., а банк начисляет на вклад 6% го­довых.

Решение:

1. Определим фактор будущей стоимости аннуитета за 4 пе­риода при ставке 6% (колонка №2) – 4,3746.

2. Рассчитаем величину накопления

350 х FVA^4(6%) = 3500 х 4,3746 = 1531 тыс. руб.

Таким образом, депонирование 1400 тыс. руб. (350 х 4) обес­печивает накопление в сумме 1531 тыс. руб. Разница представляет величину процентов, начисленных на возрастающую сумму вклада по технике сложного процента.

Периодический взнос на накопление фонда.

Символ функции – PMT/FVA.

Таблица тип В – колонка № 3.

Данная функция позволяет рассчитать величину периодически депонируемой суммы, необходимой для накопления нужной стои­мости при заданной ставке процента.

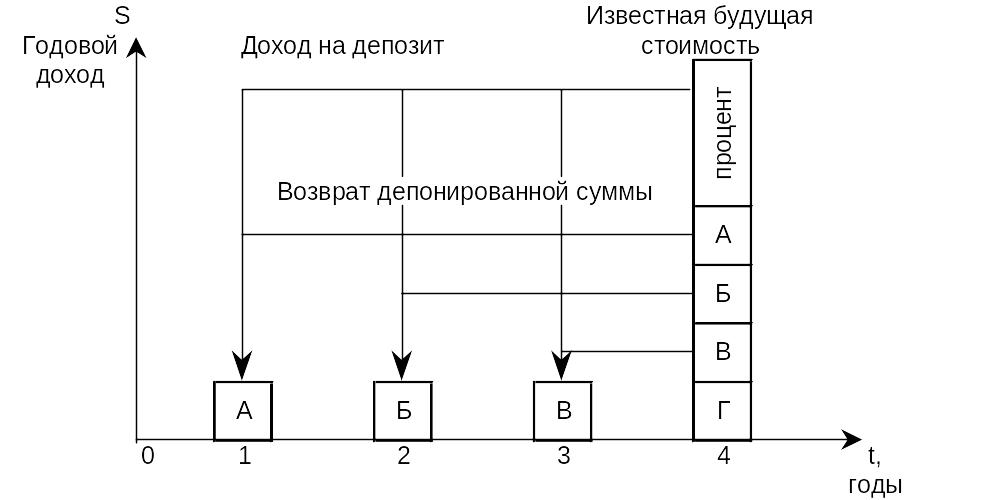
Рис. 6 Периодический взнос на накопление фонда.

Задача-алгоритм.

Какую сумму необходимо 5 раз внести на пополняемый депо­зит под 8% годовых, чтобы накопить 1700 тыс. руб.?

Решение:

1. Находим фактор периодического пятикратного взноса при 8% ставке (колонка №3) – 0,1705.

2. Рассчитаем величину депозита

1700 х PMT/FVA^5(8%) = 1700 х 0,1705 = 290 тыс. руб.

Таким образом, суммарный взнос в 1450 (290 х 5) тыс. руб. при начислении 8% годовых позволит накопить 1700 руб.

Функция «периодический взнос на накопление фонда» являет­ся обратной по отношению к функции «будущая стоимость ан­нуитета».