3.4 Проверка воспроизводимости эксперимента

То обстоятельство, что в каждой точке плана проводилось одинаковое количество опытов (в нашем случае – три), позволяет проверить однородности дисперсия. Для этого используется критерий Кохрена.

Применение этого критерия состоит в вычислении опытного значения критерия, который представляет собой отношение максимальной дисперсии в строке к сумме дисперсий во всех строках. Дисперсии вычисляются для значений опытов у_і в каждой строке плана. Затем вычисляется сумма дисперсий во всех строках, определяется максимальное значение дисперсии, которое делится на сумму дисперсий. В нашем примере

(3.6)

Теоретическое значение критерия находят по таблице приложения 1 для принятого значения уровня значимости α (обычно α = 0,05), числа степеней свободы k₁ = m - 1, и числа строк N. В нашем примере число параллельных опытов

m = 3, k₁ = 3 – 1 = 2, N = 9.

По таблице приложения 1 находим 0,4775.

Поскольку опытное значение критерия Кохрена оказалось меньше теоретического, гипотеза об однородности дисперсий замера значений функции отклика не отвергается.

3.5 Вычисление коэффициентов модели

Значения коэффициентов модели определяются по аналогии с моделью первого порядка:

(3.7)

с той лишь разницей, что знаменатель для различных коэффициентов имеет различное значение и для рассматриваемого примера составляет:

9, 6, 6, 2, 2, 4. (3.8)

Для рассматриваемой задачи формулы определения коэффициентов модели имеют вид:

(3.9)

Таким образом, уравнение математической модели примет вид

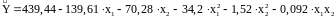(3.10)

3.6 Статистическая оценка значимости коэффициентов модели

Для статистической оценки значимости коэффициентов модели обычно составляется таблица, в которой сравниваются абсолютные значения коэффициентов сравниваются с величинами доверительных интервалов разброса коэффициентов. Для этого вычисляется дисперсия всего эксперимента как усредненное значение дисперсий по всем строкам (см. п. 1.1.8)

(3.11)

Вычисления производятся в электронной таблице.

В нашем примере

Среднеквадратичное отклонение для всего эксперимента

По таблице для критерия Стьюдента (приложение 2) при уровне значимости α = 0,05 и числе степеней свободы f₂ = N·m – 1 = 9·3 – 1 = 26 находим значение критерия Стьюдента t = 2,056.

Среднее квадратическое отклонение коэффициента модели

(3.12)

Значения определены в таблице 34

Результаты вычислений заносим в табл. 3.5

Таблица 3.5 – Статистическая оценка значимости коэффициентов модели

Коэффи- циент модели	Численное значение коэффи- циента		Среднее квадратичное отклонение коэффициента	Величина полуинтервала разброса коэффициента	Сравнение
B1	139,61	6	2,759	5,673	139,61>5,673
B2	70,283	6	2,759	5,673	70,283>5,673
B11	34,228	2	4,779	9,825	34,228>9,825
B22	1,561	2	4,779	9,825	1,561<9,825
B12	0,092	4	3,379	6,948	0,092<6,948
B0	439,44	9	2,253	4,632	439,44>4,632

Окончательно уравнение регрессии имеет вид

(3.13)