7. Вычисляем коэффициент уравнения регрессии

Для вычисления значений коэффициентов уравнения регрессии (1.1) следует вычислить для каждой строки произведения среднего значения функции отклика соответственно на величины х₀, х₁ и х₂. Затем все полученные произведения суммируются по столбцам.

Коэффициенты уравнения регрессии определяются по формулам:

(1.7)

1.8 Статистическая оценка значимости коэффициентов регрессии

Статистическая оценка значимости коэффициентов регрессии имеет своей целью исключить из математической модели второстепенные факторы, т.е. факторы, оказывающие незначительное влияние на функцию отклика. Показателем для того служит критерий Стьюдента.

Для выяснения вопроса о статистической значимости коэффициентов регрессии В_j вычисляют при заданном уровне значимости α доверительный интервал разброса среднего значения каждого из коэффициентов J_д = 2δ, и если окажется, что половина доверительного интервала превышает значение коэффициента, то это означает. что данный коэффициент незначим, и его надо исключить из математической модели. В противном случае коэффициент считается значимым.

- коэффициент незначим;

- коэффициент значим.

Величина доверительного интервала J_д = 2δ определяется подобно тому, как это делается при определении доверительного интервала разброса среднего результата случайной величины.

(1.8)

где - неизвестное истинное значение коэффициента регрессии;

- расчетное значение коэффициента регрессии;

Δ – полуинтервал разброса среднего значения коэффициента регрессии.

Величина полуинтервала определяется по формуле

(1.9)

где - среднее квадратическое отклонение всего эксперимента;

- сумма квадратов факторов матрицы планирования ;

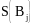- среднее квадратическое отклонение разброса коэффициента регрессии.

- критерий Стьюдента при заданном уровне значимости α. Значение критерия Стьюдента берется с учетом числа степеней свободы f.

(1.10)

где

(1.11)

где N – число различных сочетаний факторов в эксперименте;

r – число повторных опытов при каждом сочетании факторов.

В нашем примере N = 4, r = 3.

Среднее квадратическое отклонение всего эксперимента определяется по зависимости

(1.12)

(1.13)

Среднее квадратичное отклонение коэффициента регрессии

(1.14)

Критерий Стьюдента обычно вычисляется для значимости α = 0,05, что соответствует доверительной вероятности 95%.

По таблице Приложения 2 находим для значения q = 5% и f = 11 критерий Стьюдента (используется интерполяция).

Величина половины доверительного интервала по формуле (1.9)

Коэффициент В₁ уравнения регрессии не превышает значение δ, т.е. являются не значимыми.

Окончательно уравнение регрессии имеет вид

(1.15)